Технічні науки / 6. Електротехніка і
радіоелектроніка
К.т.н. Куцевол О. М., к.т.н. Куцевол М. О.
Вінницький національний аграрний університет, Україна
Розроблення адекватної
математичної моделі зерна
Відносний
кут нахилу ![]() характеристики
характеристики ![]() ,
коефіцієнт відносного приросту уявної складової струму чутливого елемента
,
коефіцієнт відносного приросту уявної складової струму чутливого елемента ![]() та відносна діелектрична проникність
та відносна діелектрична проникність ![]() [1] будуть функціями трьох змінних:
[1] будуть функціями трьох змінних:
![]() ;
(1)
;
(1)
![]() ;
(2)
;
(2)
![]() , (3)
, (3)
де ![]() – вплив температури навколишнього середовища;
– вплив температури навколишнього середовища;
![]() – вплив пористості;
– вплив пористості;
![]() – вплив вологості зерна.
– вплив вологості зерна.
Дослідження проведене для діапазону
вологостей ![]() ,
де вплив заважальних факторів найбільший, а також найбільші діелектричні втрати
та втрати від прямої провідності.
,
де вплив заважальних факторів найбільший, а також найбільші діелектричні втрати
та втрати від прямої провідності.
Складаємо
таблицю факторів для дворівневої зміни (дворівнева зміна вибрана з міркувань
обмеженості діапазону частот 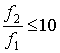 та діапазону вологостей
та діапазону вологостей 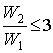 ).
).
Таблиця
факторів та рівнів їх зміни в натуральних і кодованих значеннях (табл.1).
Виходячи з даних табл.1 отримуємо трифакторний експеримент
з дворівневою зміною, для якого рівняння регресії мають вигляд [2-4]:
Таблиця 1
Фактори впливу
та рівні їх зміни
|
№ п/п |
Фактор |
Натуральне значення |
Кодоване значення |
|
1 |
Температура навколишнього середовища, 0С |
30 10 |
+1 -1 |
|
2 |
Шпаруватість, % |
40 39 |
+1 -1 |
|
3 |
Вологість, % |
28 18 |
+1 -1 |
![]() ; (4)
; (4)
![]() ; (5)
; (5)
![]() , (6)
, (6)
де ![]() – параметр
– параметр![]() ;
;
![]() – параметр
– параметр ![]() ;
; ![]() – параметр
– параметр ![]() ;
;
![]() ,
, ![]() ,
,
![]() – значення сталих складових рівнянь регресії
(4), (5), (6);
– значення сталих складових рівнянь регресії
(4), (5), (6);
![]() – вплив фіктивного параметра.
– вплив фіктивного параметра.
В
табл.2 розглядається матриця плану експеримента, в якій наявний код фіктивного
параметра, що визначає сталі складові ![]() ,
,
![]() та
та ![]() .
.
У
випадку дворівневої зміни кількість дослідів
![]() , (7)
, (7)
де ![]() – кількість факторів.
– кількість факторів.
В
даному випадку ![]() .
.
Матриця
планування при ![]() і для взаємопов’язаних факторів наведена в
табл.2.
і для взаємопов’язаних факторів наведена в
табл.2.
В табл.3 ![]() ,
,
![]() ,
,
![]() – середні значення параметрів;
– середні значення параметрів; ![]() ,
,
![]() ,
,
![]() – дисперсії параметрів.
– дисперсії параметрів.
Таблиця 2
Повний факторний експеримент
|
№ п/п |
Код |
Код |
Код |
Код |
|
1 |
+1 |
-1 |
-1 |
-1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
|
3 |
+1 |
-1 |
+1 |
-1 |
|
4 |
+1 |
+1 |
+1 |
-1 |
|
5 |
+1 |
-1 |
-1 |
+1 |
|
6 |
+1 |
+1 |
-1 |
+1 |
|
7 |
+1 |
-1 |
+1 |
+1 |
|
8 |
+1 |
+1 |
+1 |
+1 |
Таблиця 3
Результати виконання плану експеримента
|
№ п/п |
|
|
|
|
|
1 |
10,12 |
10,1 |
10,11 |
0,0002 |
|
2 |
22,88 |
22,92 |
22,9 |
0,0008 |
|
3 |
35,91 |
35,87 |
35,89 |
0,0008 |
|
4 |
50,47 |
50,49 |
50,48 |
0,0002 |
|
5 |
64,02 |
64,02 |
64,02 |
0 |
|
6 |
77,12 |
77,13 |
77,125 |
0,00005 |
|
7 |
90,04 |
90,1 |
90,07 |
0,0018 |
|
8 |
98,47 |
98,51 |
98,49 |
0,0008 |
Продовження табл.3
|
№ п/п |
|
|
|
|
|
1 |
11,31 |
11,33 |
11,32 |
0,0002 |
|
2 |
21,3 |
21,34 |
21,32 |
0,0008 |
|
3 |
31,16 |
31,12 |
31,14 |
0,0008 |
|
4 |
42,65 |
42,67 |
42,66 |
0,0002 |
|
5 |
49,03 |
49,03 |
49,03 |
0 |
|
6 |
56,43 |
56,44 |
56,435 |
0,00005 |
|
7 |
63,18 |
63,15 |
63,165 |
0,00045 |
|
8 |
67,05 |
67,01 |
67,03 |
0,0008 |
|
№ п/п |
|
|
|
|
|
1 |
2,46 |
2,45 |
2,455 |
0,00005 |
|
2 |
4,89 |
4,88 |
4,885 |
0,00005 |
|
3 |
6,53 |
6,55 |
6,54 |
0,0002 |
|
4 |
12,12 |
12,16 |
12,14 |
0,0008 |
|
5 |
35,12 |
35,1 |
35,11 |
0,0002 |
|
6 |
63,21 |
6325 |
63,23 |
0,0008 |
|
7 |
90,14 |
90,15 |
90,145 |
0,00005 |
|
8 |
122,57 |
122,5 |
122,535 |
0,00245 |
Дисперсія визначається за
виразом [3]:
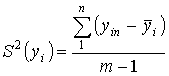 , (8)
, (8)
де ![]() – кількість дослідів.
– кількість дослідів.
Використавши дані табл.3,
визначимо значення коефіцієнтів рівнянь (4), (5) і (6), перевіримо однорідність
дисперсії експерименту, дамо статистичну оцінку значимості коефіцієнтів,
визначимо оптимальний параметр та перевіримо математичну модель на адекватність
[4-6]. Обчислення проводяться на ПЕОМ з використанням математичного пакету
MathCad 2000 Pro [7].
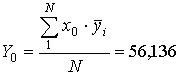 ;
; 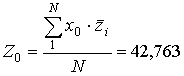 ;
; 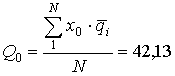 ;
;
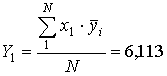 ;
;
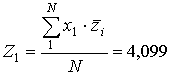 ;
; 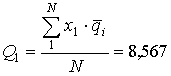 ;
;
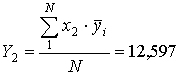 ;
; 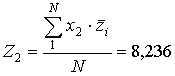 ;
; 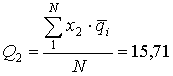 ;
;
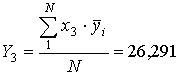 ;
; 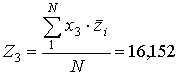 ;
; 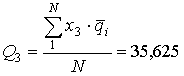 .
.
Визначення експериментальних
значень інформативних параметрів ![]() ,
,
![]() та
та ![]() здійснювалось в одних і тих же умовах з
однаковою точністю, тому можна очікувати на однорідність їх дисперсій. Щоб
переконатись у цьому, виконаємо перевірку за допомогою критерія Кохрена [3]:
здійснювалось в одних і тих же умовах з
однаковою точністю, тому можна очікувати на однорідність їх дисперсій. Щоб
переконатись у цьому, виконаємо перевірку за допомогою критерія Кохрена [3]:
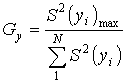 , (9)
, (9)
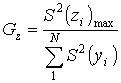 , (7)
, (7)
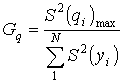 , (8)
, (8)
де ![]() – рядкова дисперсія інформативного параметра
– рядкова дисперсія інформативного параметра ![]() ;
;
![]() –
рядкова дисперсія інформативного параметра
–
рядкова дисперсія інформативного параметра ![]() ;
;
![]() –
рядкова дисперсія інформативного параметра
–
рядкова дисперсія інформативного параметра ![]() .
.
Експериментальні значення
критерію Кохрена для трьох інформативних параметрів:
![]() ;
;
![]() ;
; ![]() .
.
Табличне значення критерію
Кохрена ![]() GT
для 5%-го рівня значимості, кількості ступенів свободи
GT
для 5%-го рівня значимості, кількості ступенів свободи ![]() та кількості рядків
та кількості рядків ![]() [3] дорівнює 0,68.
[3] дорівнює 0,68.
Для всіх трьох інформативних
параметрів ![]() ,
тому твердження про однорідність дисперсій підтверджується і проведення двох
спостережень в кожному досліді цілком достатньо.
,
тому твердження про однорідність дисперсій підтверджується і проведення двох
спостережень в кожному досліді цілком достатньо.
Проведемо перевірку значимості
коефіцієнтів моделей (4) – (6) шляхом перевірки довірчого інтервалу.
Для цього спочатку знаходимо
дисперсії коефіцієнтів регресії [3]
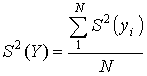 ;
;
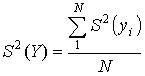 ;
; 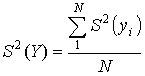 ,
,
де ![]() – рядкове значення дисперсії параметра
– рядкове значення дисперсії параметра ![]() ;
;
![]() –
рядкове значення дисперсії параметра
–
рядкове значення дисперсії параметра ![]() ;
;
![]() –
рядкове значення дисперсії параметра
–
рядкове значення дисперсії параметра ![]() .
.
Значення дисперсій
коефіцієнтів рівнянь (4) – (6), отримані експериментальним шляхом:
![]() ;
;
![]() ;
; ![]() .
.
Знаходимо довірчий інтервал
коефіцієнтів рівнянь (4) – (6):
![]() ;
; ![]() ;
; ![]() , (9)
, (9)
де ![]() – табличне значення коефіцієнта Ст’юдента. В
нашому випадку
– табличне значення коефіцієнта Ст’юдента. В
нашому випадку ![]() .
.
Експериментальні значення довірчих інтервалів:
![]() ;
;
![]() ;
; ![]() .
.
Коефіцієнти всіх трьох рівнянь значно більші їх довірчих інтервалів тому рівняння (4) – (6) остаточно записуються з їх коефіцієнтами:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() . (12)
. (12)
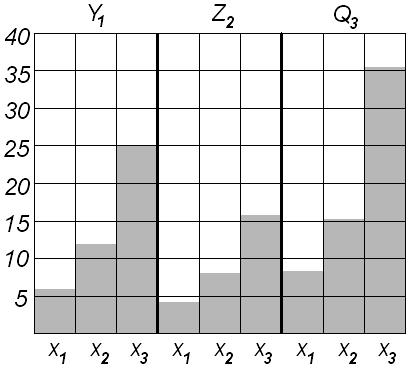
Рис.1. Порівняльна діаграма впливу на
інформативні параметри вологи і основних збурювальних факторів
Аналіз діаграм (рис.1)
показує, що досить чутливим до вологості матеріалу є параметр![]() .
Проте він не захищений від дії температури і пористості, тому не може
рекомендоватись для використання в якості інформативного. Параметр
.
Проте він не захищений від дії температури і пористості, тому не може
рекомендоватись для використання в якості інформативного. Параметр ![]() має недоліки
має недоліки ![]() та низьку чутливість до вологості. Таким
чином, оптимальним з точки зору чутливості до вмісту вологи в матеріалі та
захищеності від температури та пористості є параметр
та низьку чутливість до вологості. Таким
чином, оптимальним з точки зору чутливості до вмісту вологи в матеріалі та
захищеності від температури та пористості є параметр ![]() – коефіцієнт
відносного приросту ємнісного струму ЧЕ. Отже, математичною моделлю зразка
зерна може бути рівняння (12). Перевіримо його на адекватність, використавши
критерій Фішера [3] при заданому 5%-му рівні значимості. Експериментальне
значення критерія Фішера знаходиться за виразом:
– коефіцієнт
відносного приросту ємнісного струму ЧЕ. Отже, математичною моделлю зразка
зерна може бути рівняння (12). Перевіримо його на адекватність, використавши
критерій Фішера [3] при заданому 5%-му рівні значимості. Експериментальне
значення критерія Фішера знаходиться за виразом:
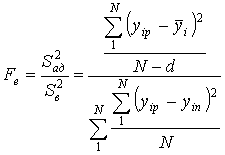 , (13)
, (13)
де ![]() – дисперсія адекватності;
– дисперсія адекватності;
![]() S2в – дисперсія
відтворюваності;
S2в – дисперсія
відтворюваності;
![]() –
розрахункові рядкові значення параметра;
–
розрахункові рядкові значення параметра;
![]() –
середні експериментальні рядкові значення параметра;
–
середні експериментальні рядкові значення параметра;
![]() –
окремі експериментальні рядкові значення параметра;
–
окремі експериментальні рядкові значення параметра;
![]() –
кількість коефіцієнтів моделі;
–
кількість коефіцієнтів моделі;
![]() –
кількість дослідів;
–
кількість дослідів;
![]() –
кількість паралельних спостережень.
–
кількість паралельних спостережень.
Розрахунок ![]() проведений на ПЕОМ із використанням
математичного пакету MathCad 2000 Pro. При цьому
проведений на ПЕОМ із використанням
математичного пакету MathCad 2000 Pro. При цьому ![]() .
.
Теоретичне значення критерія
Фішера [3] при 5%-му рівні значимості 4-х ступенях свободи ![]() .
.
Оскільки ![]() ,
можна стверджувати, що отримане рівняння регресії (12) є математичною моделлю,
адекватною об’єкту контролю з ймовірністю 0,95.
,
можна стверджувати, що отримане рівняння регресії (12) є математичною моделлю,
адекватною об’єкту контролю з ймовірністю 0,95.
Висновки
В результаті досліджень
отримано математичну модель нового інформативного параметра зерна пшениці
коефіцієнта відносного приросту уявної складової комплексного струму чутливого
елемента, адекватного об’єкту контролю із імовірністю 0,95, який має значну
захищеність від заважальних факторів і високу чутливість до вологості.
Отримана модель може бути
покладена в основу побудови та калібрування діелектрометричних вологомірів.
Література:
1. Куцевол О. М.
Високочастотні методи вимірювання вологості зерна / Олег Миколайович Куцевол,
Володимир Олександрович Поджаренко // Наук. праці Дон. Націон. техн. унів. Сер.
“Обчислювальна техніка та автоматизація”. – 2005. –Т. 2. – № 90. – С. 199–204.
2. Фрумкин Владимир Давыдович.
Теория вероятностей и статистика в метрологии и измерительной технике / В. Д.
Фрумкин, Н. А. Рубичев. – М. : Машиностроение, 1987. – 168 с.
3. Адлер Юрий Павлович.
Планирование эксперимента при поиске оптимальных решений / Юрий Павлович Адлер,
Елена Владимировна Маркова, Юрий Васильевич Грановский. – М. : Наука, 1976. –
279 с.
4. Барабащук Владимир
Иванович. Планирование эксперимента в
технике / Владимир Иванович Барабащук, Борис Петрович Креденцер, Виктор
Иванович Мирошниченко. – К. : Техніка, 1984. – 200 с.
5. Зедгинидзе Ираклий
Георгиевич. Планирование эксперимента для многокомпонентных систем / И. Г.
Зедгинидзе. – М. : Наука, 1976. – 390 с.
6. Вентцель Елена Сергеевна.
Теория вероятностей и её инженерные приложения / Е. С. Вентцель, Л. А. Овчаров.
– М. : Наука, 1988. – 480 с.
7. Дьяконов В. П. MATHCAD 8 / 2000: специальный справочник / В. П. Дьяконов. – СПб: Изд-во “Питер”, 2000. – 592 с. – ISBN 5-272-00069-2.