Физика/1. Теоретическая физика

К.ф-м.н. Галиахметов А.М., Шилкин В.А.Пасько А.А.

Донецкий национальный технический университет, Украина

Автомобильно-дорожный институт

Равновесные конфигурации скалярных частиц в

пространстве с кручениемСкалярный потенциал в одноторсионной космологии

Эйнштейна -Точно интегрируемая модель в космологии Эйнштейна – Картана

Общеизвестно, что в рамках статистического подхода в общей теории относительности (ОТО) получен ряд важных результатов (см., например, [1 - 4]). Они свидетельствуют о плодотворности метода общерелятивистской кинетики в ОТО.

Несомненный интерес представляет построение статистического подхода в актуальном варианте пуанкаре-калибровочной теории гравитации – теории Эйнштейна-Картана (ТЭК). В работе рассматриваются равновесные статистические системы бесстолкновительных скалярных частиц во взаимодействующих скалярном и векторном полях в пространстве с кручением.

Кинетические уравнения для бесстолкновительного газа скалярных частиц в ТЭК имеют вид [5]:

, (1)

где - скалярный заряд, - оператор ковариантного дифференцирования по Картану [6], - функция распределения.

Интегрируя (1) по пространству скоростей, для векторов потока числа частиц, получим

, (2)

Лагранжиан системы выбираем в виде:

(3)

Здесь - скалярная кривизна связности ; - символы Кристоффеля 2-го рода; - тензор кручения; - тензор векторного поля, ; , , - масса векторного и скалярного бозонов; - параметр взаимодействия; - инвариант векторного поля; - скалярная плотность зарядов; функция удовлетворяет условию [7]: .

Варьируя действие с лагранжианом (3) независимо по , и получаем систему уравнений ТЭК, которая совместно с уравнением Власова (1) определяет кинетику скалярных частиц во взаимодействующих скалярном и векторном полях в пространстве с кручением с фиксированной метрикой:

, (4)

, (5)

, (6)

где ; ; = ковариантный оператор в ТЭК; , , .

Из уравнений (4) и (5) получим

, . (7)

В работе рассматриваются стационарные распределения частиц, поэтому накладываются требования:

, , , (8)

где - производная Ли пространства Римана.

В пространстве Минковского , , 4 - потенциал векторного поля возьмем в виде . Из условий стационарности (8) получим , .

Полагая для простоты, что и , приведем уравнение для векторного поля (5) к виду

(9)

где .

Для больцмановской функции распределения выражения для и в пространстве Минковского были получены в работе [8]. Для системы разноименно заряженных скалярных частиц в приближении слабого поля они имеют вид:

, , (10)

где - концентрация частиц при нулевом значении скалярного потенциала; ; - модифицированная функция Бесселя.

В приближении слабого поля уравнение для скалярного поля (6) преобразуется к виду:

. (11)

Полагая в (11) и интегрируя это уравнение один раз, приходим к следующей связи между и :

, (11)

где - постоянная интегрирования.

Выбирая конкретный тип взаимодействия из (12) находим , тогда общее решение уравнения (9) имеет вид:

, (13)

где - постоянные интегрирования.

Приведем решения для наиболее интересного частного случая, когда :

1) ,

, , (14)

2) .

, (15)

3) .

, (16)

Из (14) – (16) следует, что в присутствии безмассового векторного поля для скалярного поля получено решение типа "кинк". Поскольку в рассматриваемом приближении концентрация скалярных частиц прямо пропорциональна , то, следовательно, решения (14) – (16) соответствуют равновесным кинковым конфигурациям бесстолкновительного газа.

Нетрудно провести сравнение полученных решений системы уравнений векторного (9) и скалярного (11) полей с соответствующими решениями в пространстве без кручения, как в присутствии взаимодействия , так и в отсутствии его. Результаты анализа таковы:

1) В пространстве с кручением, индуцируемым безмассовым векторным полем, при отсутствии взаимодействия между полями возможны пространственно - однородные распределения бесстолкновительного газа . Соответствующее значение векторного потенциала есть . При "включении" взаимодействия возможны как пространственно однородные распределения с тем же векторным потенциалом, так и три вида равновесных кинковых конфигураций при соответствующих значениях векторного потенциала (14), (15) и (16).

2) В пространстве без кручения в случае также возможны пространственно-однородные распределения газа. Однако при "включении" взаимодействия кинковые решения отсутствуют.

Таким образом, образование кинковых конфигураций в данном случае, может свидетельствовать о том, что статистическая система бесстолкновительных частиц находится в пространстве с кручением.

Недавние астрономические и космологические наблюдения [1, 2] свидетельствуют в пользу пространственно – плоской Вселенной, которая доминирована темной энергией и находится на стадии ускоренного расширения. Однако, в настоящее время, преждевременно полностью пренебрегать пространственной кривизной. В этой связи необходимо отметить работы (см, например, [3 - 5]). Характерная особенность современной космологии – существенно возросшая точность измерений, позволяет специалистам, работающим в этой области, говорить об эпохе "прецизионной космологии" [6, 7]. В этом контексте большой интерес представляют точные космологические решения, которые дают возможность выяснить детальную картину эволюции моделей.

В работе в рамках проблемы выбора кандидата на роль темной энергии и существования точно интегрируемых космологических моделей в теории Эйнштейна – Картана (ТЭК) с неминимально связанным скалярным полем [8-13] рассматриваются закрытые модели для духового (ghost) скалярного поля с учетом его потенциала и ультрарелятивисткого газа. Интерес к потенциалу скалярного поля V(Ф) в общерелятивистских теориях гравитации обусловлен рядом обстоятельств: его ролью в изотропизации анизотропных космологических моделей, его учетом в моделях с частицеподобными решениями; модели с V(Ф) естественно возникают в альтернативных теориях гравитации и супергравитации, в теориях струн и бран; скалярный потенциал управляет инфляцией и активно используется в моделях темной материи и темной энергии (виды применявшихся V(Ф) приведены в обзорах [14, 15]).

Точные общие решения аналогичной задачи без учета потенциала скалярного поля для произвольных значений параметра неминимальной связи ξ были получены в [16]. Было обнаружено, что для ξ > 0 решения допускают либо сингулярные модели, в которых расширение достигает максимума и затем происходит сжатие и реколлапс, либо несингулярные осциллирующие модели.

Лагранжиан модели выбираем в виде:

. (1)

Здесь R(Г) – скалярная кривизна связности ; {} – символы Кристоффеля 2-го рода; – тензор кручения; – гравитационная постоянная Эйнштейна, - лагранжиан ультрарелятивистского газа.

Отметим, что уравнение скалярного поля, соответствующее лагранжиану (1), в отсутствие кручения при ξ=1/6 и V(Ф)=0 будет конформно-инвариантным, а при ξ= –1/6, соответствует аксионному полю в ОТО [11], которое может быть ответственно за скрытую массу Вселенной.

Варьируя действие с лагранжианом (1) по получим

, (2)

, (3)

ٱ, (4)

где

,

, . (5)

Здесь ٱ – оператор Д'Аламбера в римановом пространстве, ; ; , - плотность энергии и давление ультрарелятивистского газа.

В метрике закрытых однородных изотропных моделей

(6)

для ультрарелятивистского газа справедливо

, (7)

Потенциал скалярного поля возьмем в виде

, (8)

Точное частное решение получено в квадратурах:

, , ,

, (9)

где ; ; - постоянная интегрирования;

_{; ; ;} t – космическое синхронное время , _; > 0;

Для > 3, при условии, что

решение описывает сингулярные модели с асимптотиками:

, ; , . (10)

где для , для ; .

Таким образом, учет потенциала скалярного поля создает эффект типа кривизны [12], так как эволюция моделей характерна не для закрытых, а для открытых моделей, и приводит к ускоренному экспоненциальному расширению вселенной.

Литература:

1. Иванов Г.Г. // Изв. вузов. Физика. – 1982. - № 9. – С. 42 – 48.

2. Игнатьев Ю.Г., Балакин А.Б. // Изв. вузов. Физика. – 1981. - № 7. – С. 20 – 24.

3. Захаров А.В. // Изв. вузов. Физика. – 1978. - № 3. – С. 30 – 43.

4. Захаров А.В. Макроскопическая гравитация. – М.: Янус – К, 2000.

5. Галиахметов А.М. // Изв. вузов. Физика. – 1988. - № 10. – С. 92 – 96.

6. Власов А.А. Статистические функции распределения. – М.: Наука, 1966.

7. Шикин Г.Н. Сб.: Проблемы теории гравитации и элементарных частиц. вып. 13. – М.: Энергоиздат, 1982. – С. 124 – 129.

8. Иванов Г.Г. Сб.: Гравитация и теория относительности. вып. 19. Изд-во КГУ, Казань, 1983. – С. 73 – 79.

8. Riess A.G. et al. // Astron J. – 1998. – v. 116. – P. 1009.

8. Perlmutter S.J. et al. // Astron J. – 1999. – v. 517. – P. 565.

8. G.Ellis., W. Stoerger., P. McEwan., P. Dunsby // Gen. Rel. Grav. – 2002. – v. 34. – P. 1445.

8. G. Efstathiou // Mon. Not. R. Astron. Soc. – 2003. – v. 343. – P. L 95.

8. S. del Campo., R. Herrera., J. Saaverdra // Int. J. Mod. Phys. – 2005. – v. D 14. – P. 1.

8. Melchiori A., Mercini L., Odman C.J., Trodden M. // Phys. Rev. D. – 2003. – v. 68, 043509.

8. Сажин М.В. // УФН. – 2004. – т. 174. - № 2. – С. 197 – 205.

8. Jha R., Lord E., Sinha K. // Gen. Relativ. and Gravit. - 1988. - v.20. -№6. – P. 565-571.

8. De Ritis R., Scudellaro P., Stornaiolo C. // Phys. Lett.- 1988. - v. A126.- №7. –P. 389-392.

8. Galiakhmetov A. M. // "GR 14" Abst., August 6-12 1995, Florense, Italy. - P. B75.

8. Krechet V.G., Sadovnikov D. V. // Gravitation and Cosmology. - 1997. – v.3. – № 2 (10). – P. 133 – 140.

8. Галиахметов А.М. // Изв. вузов. Физика. – 2003. – № 7. – С. 23-28.

8. Galiakhmetov A. M. // Gravitation and Cosmology. - 2004. – v.10 – № 4 (40). – P. 300 – 304.

8. Sahni V., Starobinsky A.A. // IJMP. – 2000. - v. D 9. – P. 373.

8. Peebles P.J.E., Ratra B. // Rev. Mod. Phys. – 2003. – v. 75. – P. 599.

8. Galiakhmetov A.M. // Ukr. J. Phys. – 2004. – v. 49. - № 2. – P. 105 – 109.

e – mail: ints@adi.gorlovka.net

e – mail: inst@adi.gorlovka.net

Общеизвестно, что проблемы общей теории относительности (ОТО) и стандартного космологического сценария стимулировали разработку других общерелятивистских теорий гравитации. В актуальном варианте пуанкаре калибровочной теории гравитации – теории Эйнштейна-Картана (ТЭК), в которой пространство обладает не только кривизной, но и кручением, удалось достичь некоторого прогресса в устранении трудностей ОТО (см., например, [1-4]).

В работе в рамка двухторсионной ТЭК, построенной в [5, 6], рассматриваються закрытые однородные изотропные космологические модели с неминимально связанным скалярным полем с нелинейным потенциалом,

ультрарелятивистским газом и двумя идеальными жидкостями, одна из которых моделирует материю «жесткого» типа, а вторая является источником кручения.

Лагранжиан модели L выбираем в виде суммы лагранжианов: гравитационного – , скалярного поля – , идеальных жидкостей –и , ультрарелятивистского газа - L_p

(1)

(2)

(3)

Здесь R(Г) – скалярная кривизна связности

- символы Кристоффеля 2-го рода; - тензор кручения; – гравитационная постоянная Эйнштейна ξ – постоянная неминимальной связи; V(Ф) – потенциал скалярного поля; ρ – плотность массы жидкости; П(ρ,е) – её внутренняя энергия; k, k₁, k₂, k₃– лагранжевы множители; Х – лагранжевы координаты частиц материи, e – удельная энтропия [7]; – 4-скорость; – ковариантный оператор в пространстве-времени Римана-Картана. Лагранжианы L_fl(2) для жидкости с предельно жестким уравнением состояния и L_p для

ультрарелятивистского газа не выписаны, так как для них в производной члена, регулирующего сохранение числа частиц, нет вектора кручения.

Метрический тензор g_ik имеет сигнатуру (– , – , – , + ), а тензоры Римана и Риччи определяются как. Из (3) следует, что кручение может взаимодействовать с идеальной жидкостью только через свой след (вектор кручения).

Отметим, что лагранжиан (2) в отсутствие кручения при ξ=1/6 и V(Ф)=0 соответствует конформно инвариантному скалярному полю.

Замкнутая подсистема уравнений, которая описывает в рамках ОТО гравитационное взаимодействие ультрарелятивистского газа, двух идеальных жидкостей и неминимально связанного скалярного поля с потенциалом V(Ф), соотвествующая лагранжиану L=L_g+L_s+L_fl(1)+L_fl(2)+L_P имеет вид:

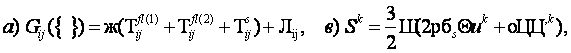
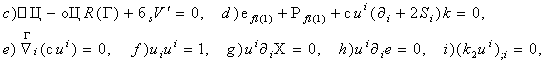
(5)

где

. (6)

Здесь – плотность энергии и давление жидкости; и – оператор Д`Аламбера и ковариантная производная в римановом пространстве, соответственно; .

Сворачивая уравнение (к) системы (5) с и учитывая соотношения (d), (f), (g) и (h), получим:

(7)

Из уравнения (d) и (e) системы (5) следует:

(8)

2.Точные космологические решения

Для пространственно – однородных изотропных моделей с метрикой

(9)

уравнения (а) и (с) системы (5) приводятся к виду

(10)

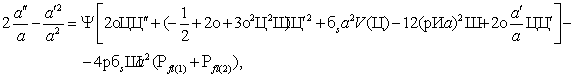
(11)

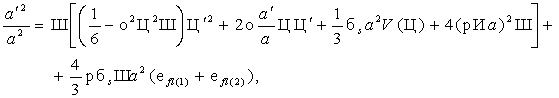
(12)

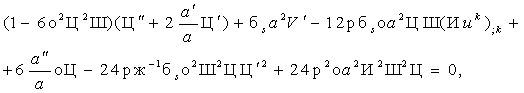
где штрих обозначает дифференцирование по η.

В дальнейшем для жидкости, которая является источником кручения, ограничимся рассмотрением вакуумного уравнения состояния: Тогда из (5) и (8) получим

(13)

где С₁, С_Θ – постоянные интегрирование (С₁>0).

Для жидкости с предельно жестким уравнением состояния

(14)

Потенциал скалярного поля V(Ф) возьмём в виде:

(15)

где μ_, λ – постоянные; β= +1 соответствует массовому скалярному полю, β= –1 отвечает нелинейности типа Хиггса.

Точные решения получены для положительных значений эффективной постоянной Эйнштейна

(16)

при условии, что

(17)

2.1. Решения для материального скалярного поля

Точные частные решения получены в квадратурах:

(18)

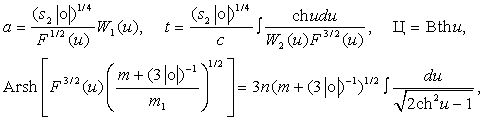
где

Для ξ>0, β= –1 функции W_i имеют вид: а анализ решения (18) показывает, что оно описывает несингулярные вселенные двух типов:

(20)

(19)

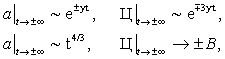
где

Для ξ<0, β= +1 функции есть В этом случае решение (18) допускает существование несингулярных моделей следующих типов: один из которых подобен (19), а второй имеет следующие асимптотики:

(21)

2.2. Решения для «гравитационного» (α_s= – 1) скалярного поля

Точное частное решения для ξ>0, β= +1 получено в квадратурах:

(22)

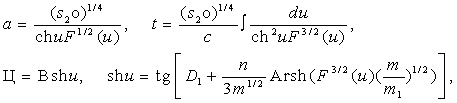
где D₁ – постоянная интегрирования.

Решение (22) получено в двух картах и описывает сингулярные модели с асимптотиками:

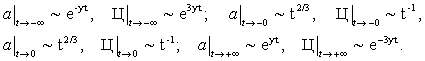
(23)

Точные частные решения для ξ<0, β= –1 запишем в виде:

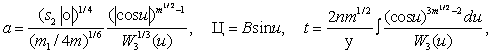
(24)

где

Анализ (24) показывает, что в этом случае все модели не имеют начальной сингулярности, а характер их эволюции определяется значением параметра :

а) <1/3. Возможны два сценария эволюции: при t→ – ∞ масштабный фактор a и скалярное поле Ф ведут себя как где а при изменяются по закону (19), и зеркальное поведение – при t→−∞ а и Ф измеряются по закону (19), а при как

в) =1/3. Решение выражается в элементарных функциях:

(25)

где

Масштабный фактор а достигает минимального значения припричём [R9C1] Для при t→ – ∞ a и Ф изменяются по закону а при как Для n= +1 имеем космологическую модель с зеркальным по отношению к n= –1 поведением.

с) 1/3< <1. Решение получено в двух картах: . Для модель сжимается по закону а затем период сжатия сменяется расширением, причем а и Ф ведут себя типу (19). Для имеет место зеркальное поведение модели.

Для =2/3 решение можно представить в элементарных функциях:

(26)

Минимум масштабного фактора достигается при причем . Заметим, что для скалярного поля Ф получено решение солитонного типа.

c)=1. Решение выражается в элементарных функциях:

(27)

Решение (27) справедливо для и получено в двух картах: n= +1 для , n= –1 для . Отметим, что всюду масштабный фактор либо убывает (n= +1), либо возрастает (n= –1), причем при t→ модели ведут себя по закону (19).

е) >1. Физически разумных решений нет.

2.3. Решения без скалярного поля

Для выяснения возможных эффектов двух источников кручения приведем точное общее решение для случая отсутствия скалярного поля:

(28)

где D₂ – постоянная интегрирования;

Из (28)видно, что сингулярное решение получено в двух картах, причем на ранних этапах эволюции масштабный фактор ведет себя как а при – по закону .

3. Выводы

Сформулируем основные результаты, полученные в данной работе:

0.В одноторсионном случае, когда источником кручения является идеальная жидкость с вакуумным уравнением состояния, получено точное общее сингулярное решение, которое имеет деситтеровскую асимптотику при t→∞.

0.В двухторсионном случае с массовым самодействующим скалярным полем (α_s= – 1, β= +1, ξ>0) найдено точное частное сингулярное решение, для которого начальный темп расширения модели меньше, чем в одноторсионном случае. Таким образом, учет второго источника кручения в виде неминимально связанного скалярного поля может приводить к замедлению начальной космологической эволюции.

0.В моделях с двумя источниками кручения возрастает число различных космологических сценариев, возможны несингулярные решения как с деситтеровской асимптотикой, так и отличной от неё. В отличие от одноторсионного случая получены модели, которые могут иметь либо больший, либо меньший темп расширения при больших значениях космологического времени.

1.Все точные решения в двухторсионном случае получены лишь при учете жидкости с предельно жестким уравнением состояния.

СПИСОК литературЫ

1.Иваненко Д.Д., Пронин П.И., Сарданашвили Г.А. Калибровочная теория гравитации. – М.: Изд-во МГУ, 1985.

1.Пономарев В.Н., Барвинский А.О., Обухов Ю.Н. Геометродинамические методы и калибровочный подход к теории гравитации. – М.: Энергоатомиздат, 1985.

1.Кречет В.Г. Проблемы гравитационного взаимодействия физических полей в пространствах аффинной связности: Автореф. дис., … д-ра физ. - мат. наук – Ярославль, 1984.

1.Галиахметов А.М. // Укр. физ. журн. – 1993. – 38,№6. – С. 807 – 814; 1994. – 39, №11-12. – С. 1029 – 1032.

1.Krechet V.G., Sadovnikov Д.V. // Gravitation & Cosmology.– 1997. – V.З. – №2(10). – P. 133 – 140.

1.Мельников В.Н., Радынов А.Г. // В сб.: Проблемы теории гравитации и элементарных частиц. Вып. 15. – М.: Энергоатомиздат, 1985. – С. 65 – 72.

Кречет В.Г., Мельников В.Н. // Изв. вузов. Физика – 1991. – 34, №2

Донецкий государственный

технический университет

Сведения об авторах

1. Галиахметов Алмаз Мансурович

Проспект Победы, 90, кв. 20 г.Горловка, Донецкая обл., Украина, 84646

Домашний телефон: 8-06242-2-14-92

Рабочий телефон: 8-06242-55-34-92

Автомобильно-дорожный институт Донецкого национального

технического университета.

завкафедрой "Общенаучные дисциплины"

к.ф. – м.н., доцент

2. Шилкин Владимир АнатольевичПасько Александр Александрович

ул. ГагаринаБессонова, 6917, кв. 2237, г. Горловка, Донецкая обл., Украина, 846274

Тел. 8-06242-553-4150-5642

Автомобильно-дорожный институт Донецкого национального

технического университета.

Студент IV курса, специальность "Автомобили и автомобильное хозяйство"

---

[R9C1]