УДК                                                                                            НТУ “ХПІ”

Проф. Матієга В.М.

Аспірант  Даналакій О.Г.

 

НЕКОТОРЫЕ   МОДЕЛИ   СТАЦИОНАРНЫХ   ТЕРМОЭЛЕКТРИЧЕСКИХ   ХОЛОДИЛЬНИКОВ

Предложены холодильники на поперечном эффекте Пельтье или Эттингсгаузена, работающие в адиабати­ческих условиях, а также холодильник на эффекте Томсона.

Анизотропный термоэлектрический холодильный элемент и холодильный элемент Эттингсгаузена отли­чаются тем, что одна из боковых граней термостатирована [1, 2]. При этом подразумевается, что она находится в идеальном тепловом контакте с термостатом и вместе с тем электроизолирована от него. Эти два требования в данном случае противоречат одно другому. Поэтому встает вопрос о создании такой конструкции, в которой бы не было необходимости в термостатировании боковой грани. С этой целью в данной работе предложены холодильные элементы, рабочими эффектами которых являются поперечный эффект Пельтье или эффект Эттингсгаузена, а боковые грани адиабатически изолированы от внешней среды.

Рассмотрена также возможность создания холодильника на эффекте Томсона.

1. Адиабатический анизотропный холодильный элемент (АХЭ). В качестве материала АХЭ выберем термоэлектрически-анизотропный однородный полупроводник с не зависящими от температуры кинетичес­кими коэффициентами. Тогда уравнение теплопроводности можно записать в виде

 

                                    ,                                                                (1)

Где температура считается двумерной (рис. 1). Граничные условия

                                  T (0,y) = T (l,y) = T0,                                                        (2)

                                                                                                  (3)

Условия (2) означают термостатирования торцевых граней АХЭ при температуре Т0, а (3) – адиабатическую изоляцию нижней и верхней граней.

         Решение управления (1) при условиях (2), (3) легко найти методом Фурье. Оно имеет вид

T (x, y) = T0 -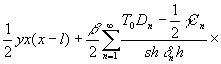

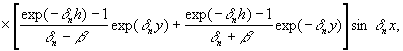
где Dn=2(1-(-1)n)/(nπ), Cn=-4l2(1-(-1)n)/(nπ) – коэффициенты разложения 1 и функции  в ряды Фурье по синусам.

         Распределение температуры на грани y=0 такое:

.

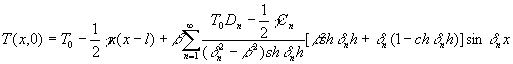Охлаждение будет иметь при условии, что третий член в последнем выражении отрицательный.

         Оценим температуру в точке , если ток течет в отрицательном направлении оси   (рис. 1). Пусть α12=10-4 В/К, χ=10-2 Вт / (см·К), ρ=10-3 Ом·см, δnh≥3. Получим.

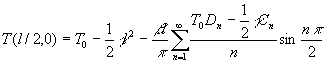.                                           (4)

 

 

 

 

 

 

 

 

 

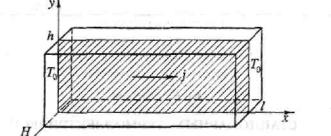
Рис. 1. Принципиальная схема адиабатического АХЭ или ХЭ Эттингсгаузена (в случае ХЭ Эттингсгаузена: х – треугольная, y-бинарная, z- биссекторная оси). Грани y=0 и y=h диабатически изолированы от внешней среды

 

Последнее выражение написано при условиях, что sh  δnh ≈ ch δnh >> β. Пусть T0=300 K, jl=60 А/см, согласно (8),  К, т.е. снижение температуры составляет 30К.

         2. Адиабатический холодный элемент (ХЭ) Эттингсгаузена. ХЭ Эттингсгаузена на образцах с термостотированой гранью исследовался, например, а [3-8]. В качестве материала ХЭ использовался Ві и славы BiSb. Ток был направлен вдоль тригональной, магнитное поле – вдоль биссекторной, а перепад температуры – вдоль бинарной осей. Эффект охлаждения Эттингсгаузена интересен тем, что может применяться в области криогенных температур. Автор настоящей статьи тоже внес определенный вклад в исследование эффекта Эттингсгаузена на образцах с термостатированой боковой гранью [90]. Выше мы отмечали, что надежный тепловой контакт грани с термостатом трудно осуществить.

         Пусть ХЭ указанной выше ориентации изготовлен из монокристалла Ві. Считая, что кинетические коэффициенты материала ХЭ не зависят от координат и температуры, теплопроводности изотропна, направим ток в доль тригональной, магнитное поле – вдоль биссекторной оси (рис. 1). Тогда управление теплопроводности запишется в виде

                           (5)

Граничные условия

                                     (6)

                                               (7)

Решения управления (5) при условиях (6),(7) будем таким:

 

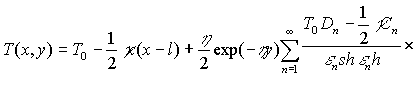
  где   и   определены в п.1. Оценим температуру в точке  по формуле

При условии, что  и см, последнее выражение будет иметь вид

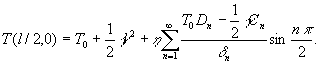
         Для численной оценки выберем такие параметры: ρ=10-3 Ом·см, QH=2·10-4 B/К, χ=10-3Вт / (см·К), j= -16 А/см2, Т0=80 К. Получим  =72 К. Дальнейшая работа над адиабатическим ХЭ Эттингсгаузена должна состоять в оптимизации параметров (материал, размеры, ток и т. д.).

         3. Модель ХЭ на эффекте Томсона. Эффект Томсона (ЭТ) состоит в выделении (поглощении) тепла в объеме неизотермической проводящей среды, через которую протекает электрический ток. В единице объема  выделяется (поглощается) тепло [10]

qТ

 

 

Рис. 2. Принципиальная схема термоэлектрического холодильника Томсона: 1- обра­зец; 2 – токопровады к образцу.

ЭТ был открыт давно [11], но не нашел практического применения.

Ниже предложена феноменологическая модель стационарного холодильника на ЭТ, в которой градиент температуры и электрический ток совпадают по направлению. Положив, что удельное сопротивление и теплопроводность материала ХЭ, а также производная da/dT постоянны и что распределение температуры одномерно, запишем уравнение теплопроводности в стационарном случае в виде

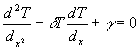                                         (8)

И рассмотрим совместно с граничными условиями

                                                   (9)

Для решения этой задачи используется метод сеток [12], согласно которому производные заменяются их приближенными значениями, выраженными через разности значений функции в отдельных дискретных точках-узлах. Дифференциальное уравнение в результате таких преобразований заменяется эквивалентными соотношениями в конечных разностях.

Прежде чем приступить к численным оценкам температуры в отдельных точках, отметим, что задача будет тем точнее решена, чем больше будет число разбиений длины образца на равные отрезки, т. е. чем меньше будет р. Однако при большом числе разбиений нужно использовать ЭВМ, что приведет к потере аналитичности. Поэтому мы ограничимся небольшим числом разбиений, считая, что длина ХЭ не очень большая.

Разобьем длину ХЭ на четыре равные части. Тогда уравнения (8) и (9) приводят к системе уравнений относительно Тх, Т2, Т3 (рис. 2)

 

из которых найдем

    

    

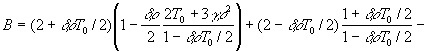
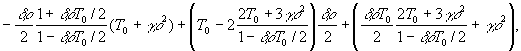
Произведем численную оценку температур Т1, Т2,  Т3.  Положим l=1см, T0=300 K, ρ=10-3 Ом·см, χ=10-2 Вт/(см·К), da/dT=10-4 B/K2, j=0.15 А/см2. Для этих параметров будем иметь: γ=2.3·10-3, К/см2, δ=1.5.10-3 (К·см)-1, δρТ0/2=0.056. Поскольку δρТ0/2«1, приближенно получим: А=2δρ, В = 4, С = -4Т0, и соответственно Т3 = Т0(1 - δρТ0/4), Т1 = Т0(1 + δρТ0/4), Т2 = Т0(1 - δρТ0/2). Температу­ра Т2 = 280 К. Таким образом, в рассматриваемом случае имеем снижение температуры на 20 К.

Обратим внимание на следующее обстоятельство. Если в выражениях  для Т1, Т2, Т3 заменить j на (-j), то они станут другими, что очевидно противоречит физической ситуации. Например, ясно, что Т2 не должна зависеть от направления тока. Это противоречие снимается, если учесть, что при замене j на (-j) изменяется также и знак производной dT/dx, так что произведение jdT/dx в уравнении (8) знак не меняет. При этом

 

 

 

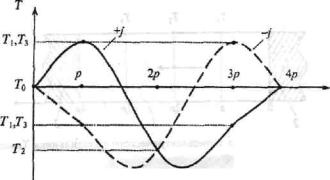Рис.3. Распределение температуры в образце холодильника Томсона при прямом (+j) и обратном (-j) направлениях электрического тока

 

Т1 и Т3 меняются местами, а Т2 остается тем же. Качественно зависимость Т(х) показана на рис. 3, откуда видно, что точка, в которой имеет место минимальная температура, может быть смещена относительно х = 2р.

         Приведенные расчеты носят иллюстративный характер и призваны показать, что ЭТ может служить для целей охлаждения. Дальнейшая работа должна быть направлена на поиск оптимальных материалов, токов, размера образца, что не является предметом настоящего исследования.

         Обозначения

Т - температура; х, у, z - оси декартовой системы координат; h - высота; l- длина ХЭ; β=α12j/х; α12 -коэффициент поперечной термоэдс; εп=;; п = 1, 2, 3, ... - индекс суммирования; η = QHj/x; Q - коэффициент Нернста; Н - напряженность магнитного поля; δ= (da/dT)j/χ; у = ρj2/ χ; α - термоэдс, зависящая линейно от температуры; ρ и χ - удельные сопротивление и теплопроводность; j - плотность тока; qT - объемная плотность тепла Томсона; р = l/4; T1, Т2, Т3 - температуры точек в ХЭ Томсона; Т0 - температура термостата.

 

 

 

 

Литература

1.     Осипов Э.В. Твердотельная криогеника. Киев, 1977.

2.     Орхем В.Г. // ИФЖ. 1981. Т. 40, № 1. С. 75-81.

3.     Анатычук Л.И. Термоэлементы и термоэлектрические устройства. Киев, 1979. С. 28-30.

4.     Панов Д.Ю. Справочник по численному ришению дифференциальных уравнений в частных производных. М., 1951.

5.     O'Brien B. J., Wallace С S. //— J. Appl. Phys., 1958, vol. 29, p. 1010—1012.

6.       Kooi C. F. Wallace C.S. //— J. Appl. Phys., 1963, vol. 34, p. 1735—1742.

7.     Gurthie G. L. //—J. Appl. Phys., 1965, vol. 36, p. 3118—3122.

8.   Harman Т. С., Honig Т. M. Thermoelectric and thermomagnetic effects and appli­cations.—N. Y., McGraw-Hill, 1967.—377 p.

9.   Harman Т. С., Honig Т. M. Thermoelectric and thermomagnetic effects and appli­cations.—N. Y., McGraw-Hill, 1967.

10. Иоффе А.Ф. Полупроводниковые термоэлементы. М.-Л., 1960. С. 7-14.