![]()
![]()
![]()
![]() ИНЖИНЕРНЫЕ ФИНАНСОВЫЕ РАСЧЁТЫ
ИНЖИНЕРНЫЕ ФИНАНСОВЫЕ РАСЧЁТЫ
НА
БАЗЕ MATLAB
![]()
Юрий ВАСИЛЮК, Александр
ОСТАНИН
Политехникa Бeлоcтoцкaя, Институт
Информатики
e-mail: jerzy.wasiluk@onet.eu,
aleks@ii.pb.bialystok.pl
АННОТАЦИЯ
Данная работа посвящена
проблемам реализации методов, алгоритмов и программного обеспечения для
инжинерных финансовых расчётов на базе современной математики и системы
МАТЛАВ. Показано, как с помощью пакета
прикладных программ Financial Toolbox могут
быть выполнены задачи, возникающие в процессе математического моделирования и
анализа финансовых приложений. Приводятся результаты компьютерного
моделирования типовых задач экономики.
1. ВВЕДЕНИЕ
Система МАТЛАВ и пакеты
прикладных программ для финансовых расчётов Financial Toolbox (ППП FT) находят
применение в разных сферах науки – начиная от математики, экономики, вплоть до
наук биологических. Благодаря доступу к производительным вычислительным
алгоритмам и механизмам анализа результатов система МАТЛАВ позволяет
быстро и эффективно производить сложные вычисления, поддерживаемые
высокоуровневой графикой. С помощью ППП FT могут быть выполнены
следующие задачи:
·
подсчёт и анализ
цен и облигаций;
·
анализ портфелей
ценных бумаг;
·
оценка стратегии
методов хеджирования;
·
идентификация, измерение и контроль рисков;
·
анализ и высчисление
денежных потоков;
·
анализ
экономической активности;
·
создание
структурных финансовых инструментов валютного обмена;
·
моделирование
методом Монте-Карло и прогнозирование;
·
GARCH - процессы;
·
проведение исследовательских работ в области финансовой аналитики.
В приведенном ниже материале
представлены примеры использования некоторых отдельных функций ППП FT.
1. ВЫЧИСЛЕНИЕ
СТОИМОСТЕЙ ЦЕННЫХ БУМАГ
Ряд функций ППП FT предназначены для оценивания облигаций, вычисления доходностей и котировок, определения временных факторов и накопленного
процента, расчета купонных дат, а также показателей
дюрации и выпуклости. К этим функциям в ППП FТ
относятся m-функции
bndprice, bndyield, bndconvp, bndconvu, bnddurp, bndduru. В качестве входных параметров для всех этих функций может
служить стандартное множество входных
аргументов:
Settle - дата расчётная;
Maturity - дата погашения;
Period - период купонных
оплат;
Basis - базис расчёта дней;
EndMonthRule - правило конца месяца;
IssueDate - дата выпуска
облигации;
FirstCouponDate - первая купонная дата;
LastCouponDate - последняя купонная дата.
Из общих
входных аргументов только Settle и Maturity - обязательные, а все
остальные являются необязательны ( их значения устанавливаются по умолчанию). Для
FirstCouponDate и LastCouponDate значения по умолчанию не
применяются. Поэтому, если эти параметры не были заданы, это означает, что облигация
не имеет нестандартного первого или последнего купонных периодов. В этом случае
облигация является облигацией со структурой купонных платежей, основанной
исключительно на дате погашения.
Для иллюстрации
использования аргументов по умолчанию рассмотрим m-функцию cfdates, которая вычисляет даты
денежных потоков для портфеля ценных бумаг с фиксированными поступлениями
независимо от того, является первый или последний
купонный период нормальным, длинным или коротким.
Синтаксис обращения к функции при полном списке
входных аргументов имеет вид:
CFlowDates=cfdates(Settle, Maturity,
Period, Basis, EndMonthRule,… IssueDate,FirstCouponDate, LastCouponDate)
Минимальное обращение нуждается только в расчётной дате и дате погашения:
CFlowDates=cfdates(Seattle,
Maturity)
Пример 1:
Облигация имеет следующие характеристики:
Settle
= '20-sep 1999'
Maturity
= '15-Осt-2007'
Period
= 2
Basis
= 0
EndMonthRule
= 1
IssueDate
= NaN
FirstCouponDate
= NaN
LastCouponDate = NaN
В этом примере Period и EndMonthRule заданы как значения по умолчанию, а IssueDate, FirstCouponDate и LastCouponDate определены как NaN. Присвоение IssueDate, FirstCouponDate и LastCouponDate значения NaN в этом примере означает
передачу функции cfdates
информации, что облигация выпущена до расчетной даты и отсутствуют нестандартные первый или последний купонные периоды.
При установке указанных значений все приводимые обращения дают один и тот же результат. В итоге, оставляя один входной параметр неопределённым, мы получим тот же эффект, как и в передаче его в виде пустой матрицы [] или NaN, потому что всё три варианта указывают m-функции cfdates на необходимость использования для данного параметра значения по умолчанию.
Пример 2:
Предположим, что мы имеем портфель с
двумя облигациями:
Settle
= ’20-sep-1999’
Maturity=['15-Осt-2007';'15-Осt-2010']
Для всех представленных ниже
обращений к cfdates
определено значение купонного периода
как значения по умолчанию.
cfdates(Settle,Maturity,2)
cfdates(Settle,Maturity,[2
2])
cfdates(Settle,Maturity,[])
cfdates(Settle,Maturity,NaN)
cfdates(Settle,Maturity,[NaN
NaN])
cfdates(Settle,Maturity)
Первые два обращения явно задают Period = 2, при этом первое обращение определяет одно значение 2 для всех
купонных периодов. При втором обращении также
используется значение: купонного периода
по умолчанию, так как явно был задан вектор из двух компонентов, равных
2. При третьем обращении передается пустая матрица [], которая интерпретируется как неприемлемое значение периода, которое
необходимо заменить на значение по умолчанию. Четвертое обращение аналогично
предыдущему за исключением того, что передается NaN.
Пятое обращение передает два значения NaN и оказывает такое же действие, как и третье обращение. Последнее обращение передает минимальное входное множество.
Рассмотрим еще два обращения
к m-функции cfdates для того же портфеля из двух облигаций:
cfdates
(Settle, Maturity, [4 NaN])
cfdates (Settle, Maturity, [4 2]),
первое из которых устанавливает Period = 4 для первой облигации и неявно устанавливает значение по умолчанию Period = 2 для второй облигации; второе
обращение имеет то же самое действие, что и первое, но периоды были
установлены явно для обеих облигаций.
2. АНАЛИЗ ПРОТЕКАНИЙ ДЕНЕЖНЫХ ПОТОКОВ
С помощью функций оценки денежцых потоков и функций
финансового учета можно выполнять стандартные вычисления, связанные с денежными
потоками. Ниже показан пример, в котором используется прибыльный денежный
поток: начальные инвестиции $20 000
сопровождаются тремя выплатами годового дохода, за повторными инвестициями в $5 000 следуют еще 4 выплаты прибыли.
Инвестиции - отрицательные, платежи, выплаты
доходов - положительные (рис .1):
stream
=[-20000,2000,2500,3500,-5000,6500,9500,9500,9500];
plot (stream)
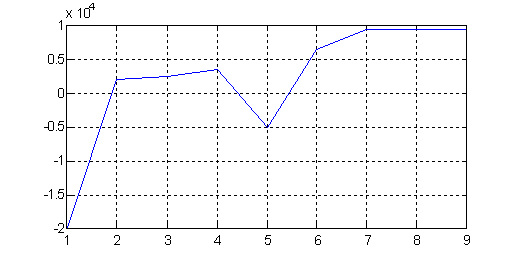
Рис. 1. Протекание денежных потоков
3. ПРОЦЕНТНЫЕ
СТАВКИ
Ряд функций ППП FT
предназначены для исчислений процентных ставок, связанных с денежными потоками.
К примеру, чтобы высчислить внутреннюю ставку доходности денежного потока,
нужно было выполнить функцию irr:
ror = irr (stream),
ror =
0.1172,
которая
для изображённого выше потока возвращает значение ставки рентабельности, ровное
11.72%. Необходимо отметить, что оценка
внутренней ставки доходности денежного потока может быть неоднозначной. Каждый
раз, когда в денежном потоке меняется знак, определяющее функцию irr,
уравнение может приводить к двум дополнительным ответам. Связанные с
выполнением данной функции вычисления требуют решения алгебраического уравнения
степени n, и число
действительных корней такого уравнения может зависеть от числа изменений знаков
входящих в него коэффициентов. Уравнение для внутренней ставки
доходности выглядит следующим образом:
сf![]() /(1 + r) + сf2 /(1
+ r)2 +... + сfп /(1
+ r)n + Investment
= 0,
/(1 + r) + сf2 /(1
+ r)2 +... + сfп /(1
+ r)n + Investment
= 0,
где сfn -
денежный поток в n-м периоде; n - число
периодов; Investment (отрицательное)- начальные денежные издержки в
момент времени 0. В принципе irr
идентифицирует такую ставку r, при которой текущая
стоимость нетто денежного потока равна начальным инвестициям. Если все сfn положительны, то имеется только одно решение.
Всякий раз, когда знак коэффициентов изменяется, возможно появление двух или
менее дополнительных действительных корней
Другая
функция, effrr высчисляет
эффективную ставку рентабельности при заданной годовой ставке (известной также
как номинальная ставка или годовая процентная ставка) и определенном числе
периодов начисления сложных годовых процентов. Для определения эффективной
ставки основываясь на годовой процентной ставке, ровной 9%, с ежемесячными
сложными процентами, достаточно записать:
rate = effrr(0.09,
12),
rate =
0.0938
т.е. в ответе будет: 9.38%.
4. ВЫЧИСЛЕНИЕ ТЕКУЩИХ И БУДУЩИХ СТОИМОСТЕЙ
Пакет Financial Toolbox включает в свой состав
функции вычисления текущих и будущих
стоимостей денежных потоков при регулярных
или нерегулярных интервалах времени с равными или неравными платежами: fvfix, fvvar, pvfix i pvvar. Функции fix подразумевают равные денежные потоки с
регулярными интервалами, а функции var допускают нерегулярные потоки при нерегулярных периодах.
Для
типового потока, для которого выше была вычислена внутренняя ставка доходности,
с помощью одной из рассматриваемых функций можно вычислить текущую чистую
стоимость. Обращение к функции
npv = pvvar(stream, ror)
даёт
результат, ровный 2.6830e-011, или 0.000000000026830, близкий нулю (обычно
результат вычислений не равен точно нулю из-за погрешностей округления).
ППП FT позволяет для денежного
потока вычислять также дюрацию Маколея, которая определяет насколько долго, в
среднем, владелец ждет получения платежа. Функция cfdur вычисляет дюрацию Маколея и модифицированную дюрацию
денежного потока. Задавая
величину учетной ставки 6%
rate=0.06;
[duration,
moddur]=cfdur(stream, rate),
получим,
что дюрация равна 23.49 периода, а модифицированная дюрация -22.16 периода.
Продолжительность этих периодов та же самая, что и периодов в денежном потоке.
Трёхмерная
графика MATLABa позволяет
пользователю также визуализоватъ ландшафт риска процентной ставки отвечающий
портфелю облигации во времени (рис.2).
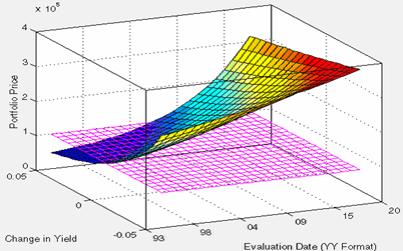
Рис. 2. Ландшафт
риска процентной ставки портфеля во
времени
5. ВЫЧИСЛЕНИЕ АМОРТИЗАЦИОННЫХ ГРАФИКОВ
Функции ППП FT для
расчета стандартных амортизационных графиков позволяют вычислять и полный
амортизационный график актива с возвращением остаточной стоимости после его
применения.
Ниже приведен пример амортизации автомобиля стоимостью $15000 в пределах пяти лет с ликвидационной стоимостью $1500. Вычисляется износ в соответствий с сокращающейся балансовой стоимостью при двух значениях ставок расчета норм амортизационных начислений: 50% (фактор износа с сокращающейся балансовой стоимостью равен 1.5) и 100% (фактор износа с сокращающейся балансовой стоимостью равен 2.0 ). При выполнении команд
decline1=depgendb(15000,1500,5,1.5)
decline1=depgendb(15000,1500,5,1.5),
мы получаем результат (рис.3 а, б):
decline1=
4500.00 3150.00 2205.00 1543.50 2101.50
decline2=
6000.00 3600.00 2160.00 1296.00
444.00
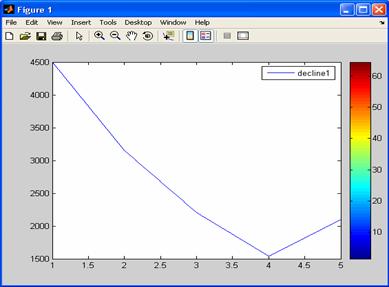
a)
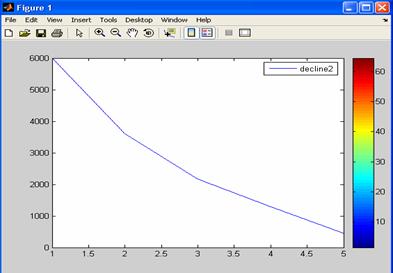
б)
Рbс. 3. Изменение амортизационных начислений
Эти функции возвращают фактическую величину
амортизационных начислений в течение первых четырех лет, а также величину
остаточной стоимости на начало пятого года.
6. ВЫЧИСЛЕНИЕ
РЕНТЫ
Несколько функций ППП FT относятся
к аннуитетам, определяемым как регулярно поступающие в течение установленного
периода времени платежи в обмен на единовременно внесенную первоначальную
сумму.
В примере 3 показано, как
можно вычислить процентную ставку, когда известны только величины платежей и
основная сумма займа.
Пример 3:
Для ссуды, основная сумма которой составляет $5000.00, а
погашение производится ежемесячно выплатами $130.00 в течение четырех лет, процентная
ставка определяется следующим образом:
rate=annurate(4*12,130,5000,0,0).
Функция возвращает значение ежемесячной ставки, равное
0.0094, или ежегодную ставку около 11.28 %.
Пример 4 использует функцию оценки текущей стоимости, чтобы показать, как вычислить первоначальную основную сумму займа, когда известны размеры платежей и ставка.
Пример 4:
Для займа, который
погашается ежемесячными платежами в $300.00 при годовой процентной ставке в
11%,
principal=pvfix(0.11/12,4*12,300,0,0).
Функция возвращает первоначальное значение основной суммы
займа, равное $11607.43.
Следующий пример иллюстрирует вычисление
амортизационного графика займа, или аннуитета.
Пример 5:
Первоначальная
стоимость аннуитета составляет $5000.00 и погашается в течение
12 месяцев при ежегодной ставке 9%:
[Prpmt,intpmt,balance,payment] = amortize(0.09/12, 12,
5000, 0, 0);
Функция возвращает векторы, содержащие размеры платежей по основной сумме
займа (рис. 4):
Prpmt=[399.76 402.76 405.78 408.82 411.89 414.97 418.09 421.22 ... 424.38 427.56
430.77 434.00],
размеры процентных платежей:
intpmt=[37.50 34.50
31.48 28.44 25.37 22.28 19.17 16.03
12.88 9.69 ...
6.49 3.26 0.00],
балансовый остаток для каждого периода: '
balance=[4600.24 4197.49 3791.71 3382.89
2971.01 2556.03 2137.94 ...
1716.72 1292.34 864.77 434.00 0.00]
а также скаляр, определяющий величину ежемесячных
платежей
payment
= 437.26.
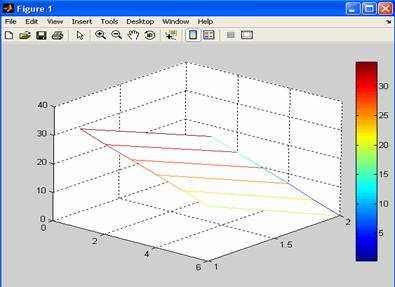
Рис.4. Амортизационный график займа
6. ВЫВОДЫ
В работе представлены некоторые примеры финансовых вычислений с
использованием системы MATLAB. Благодаря возможностям среды программирования
этой системы возможно создание собственных процедур и функций, специфичных для
данной сферы приложений.
Использование пакета Financial Toolbox фирмы MathWorks, Inc
для расчета показателей движения денежных средств и других данных позволяет
вычислять процентные ставки по займам и кредитам, коэффициенты рентабельности,
кредитные поступления, оценивать и прогнозировать стоимость инвестиционного
портфеля, вычислять показатели износа и т.п.
Эластичность программирования в системе MATLAB, интерактивный доступ к современным и надёжным
численным алгоритмам линейной алгебры, математического анализа и матричных
вычислений в соединении с компьютерной
графикой показали, что есть это идеальный инструмент для работы в сфере
финансовой аналитики.
7. ЛИТЕРАТУРА
[1] Лавров К.Н., Цыплякова Т.П.: Финансовая аналитика. М., Диалог-МИФИ, 2001
[2] Хазанова Л.Э.: Математическое моделирование в экономике.
М., БЕК, 1998
[3] Елисеева И.И.: Эконометрика.
М., Финансы и статистика, 2001
[4] Первозванский А.А., Первозванская Т.Н.: Финансовый рынок: расчет и риск.
М., Инфра-М, 1994
[5] Шведов А.С.: Теория эффективных
портфелей ценных бумаг. М., ГУВШЭ, 1999
[6] Цисарь И., Нейман В.: Компьютерное моделирование экономики., М., Диалог-МИФИ, 2002
[7] Мур Д., Уэдерфорд Л.Р. и др.: Экономическое
моделирование в Microsoft
Excel,
6-е изд., М., Изд. ” Вильямс ”, 2004
[8] Brealey R.A., Richard A., Myers S.C.: Principles
of Corporate Finance, 4th ed. New York, McGraw-Hill, 1991
[9] Bodie Zvi, Kane A.,
Markus A.J.: Investments, 2nd ed. Burr Ridge III., Irwin., 1993
[10] Daigler
R.T.: Advanced Options Trading. Chicago, Probus Publishing Co., 1994
[11] Dictionary of Finance. Oxford University Press, 1993
[12] Fabozzi F.J., Fabozzi T.D., eds.: The
Handbook of Fixed-Income Securities, 4th ed. Burr Ridge III., Irwin., 1995
[13] Hamilton J.D.: Time Series Anlysis.
Princeton University Press, 1994
[14] Markowitz H.M.: The Optimization of the
Quadratic Function Subject to Linear Constaints. // Naval Reseach Logistic
Quarterly. V. 3, 1956
[15] Marshall J.F., Vipul K.B.: Financial
Engineering: A Complete Guide to Financial Innovation, New York Institute
of Finance, N.Y., 1992
[16] Welfe A.: Ekonometria. Metody i ich zastosowanie. PWE, Warszawa, 2003
[17] Strahl D., Sobczak E., Markowska M., Bal-Domanska B.: Modelowanie ekonometryczne z EXCELEM. Wydawnictwo AE we Wrocławiu, Wrocław, 2004
[18] Sharpe W.F.: Macro-Investment
Analysis. An “electronic work-on-progress” published on the World Wide Web,
1995, at http://www.stanford.edu/~wfsharpe/mia/mia.htm
[19] Sharpe W.F., Gordon J.A.: Investments, 4th ed.,
Englewood Cliffs, N.J., Prentice Hall, 1990
[20] Financial Toolbox User’s Guide. The Math
Works, Inc. 2000-2007
[21] GARCH
Toolbox User’s Guide. The Math Works, Inc. 1999-2007
[22] http://www.mathworks.com - Domowa strona MATLAB’a, zawierająca dokumentację o środowisku programistycznym