Шанкибаев
Б.Н.
Республика
Казахстан
Центрально-Азиатский
университет
Условие оптимальности решения
целочисленной распределительной задачи
В данной статье главе рассматривается целочисленная распределительная задача, [1], [2], в следующей постановке: найти наименьшее значение функции
![]() (1)
(1)
при ограничениях:
![]() (2)
(2)
![]() (3)
(3)
![]() .
(4)
.
(4)
Предполагается, что все ![]() и
и ![]() неотрицательные и
целые.
неотрицательные и
целые.
Учитывая, что
распределительную задачу можно представить как обобщённую транспортную задачу
на простой сети, будем множество индексов ![]() и
и ![]() именовать узлами, а
всякое решение
именовать узлами, а
всякое решение ![]() задачи называть
потоком. С другой стороны, так как описываемый алгоритм использует табличную
форму записи, то множество индексов
задачи называть
потоком. С другой стороны, так как описываемый алгоритм использует табличную
форму записи, то множество индексов ![]() будем называть
строками таблицы, а множество индексов
будем называть
строками таблицы, а множество индексов ![]() - столбцами.
- столбцами.
Примем обозначения:
1. ![]() - наименьшее целое
неотрицательное число, большее дроби
- наименьшее целое
неотрицательное число, большее дроби ![]() ;
;
2. ![]()
3. ![]()
Пусть  - некоторое решение
задачи (1) - (4); выясним условия оптимальности этого решения.
- некоторое решение
задачи (1) - (4); выясним условия оптимальности этого решения.
Возьмём произвольную
последовательность узлов ![]() , образующих множество
, образующих множество ![]() , пронумерованных в указанном порядке. Далее, пусть
, пронумерованных в указанном порядке. Далее, пусть ![]() последовательность
узлов таких, что
последовательность
узлов таких, что ![]() . Каждой паре
. Каждой паре ![]() поставим в
соответствие целые числа
поставим в
соответствие целые числа ![]() , удовлетворяющие условию
, удовлетворяющие условию
![]() , (5)
, (5)
где
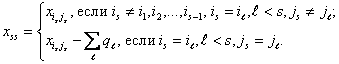
Обозначим:
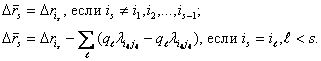
Определение. Множество ![]() - допустимый набор
узлов (д.н.у.), если найдутся целые числа
- допустимый набор
узлов (д.н.у.), если найдутся целые числа ![]() , удовлетворяющее условию (5), такие, что:
, удовлетворяющее условию (5), такие, что:
а) 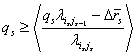
для наибольшего
порядкового номера ![]() узла
узла ![]() из множества
из множества ![]() ;
;
б)
![]() .
.
Пусть ![]() - д. н. у. Назовем
перестановкой потока по данному д.н.у. следующую операцию: поток
- д. н. у. Назовем
перестановкой потока по данному д.н.у. следующую операцию: поток ![]() уменьшен, а поток
уменьшен, а поток ![]() увеличен на величину
увеличен на величину ![]() .
.
Справедлива следующая лемма.
Лемма.
Перестановка потока
по допустимому набору узлов переводит одно допустимое решение задачи (1)-(4) в другое.
Доказательство. Выполнение условий (3) и (4) непосредственно следует из
характера перестановки и определения чисел ![]() . Покажем, что поток
. Покажем, что поток ![]() , полученный в результате перестановки, удовлетворяет условию
(2) для всех
, полученный в результате перестановки, удовлетворяет условию
(2) для всех ![]() .
.
Из
пункта «а» определения I для любого узла ![]() из набора по
наибольшему номеру
из набора по
наибольшему номеру ![]() , с которым входит данный узел в указанный набор, имеем
, с которым входит данный узел в указанный набор, имеем
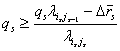 .
.
Отсюда
![]() ,
,
где
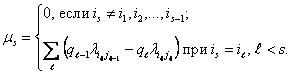
Далее,

Аналогично,
из пункта «б» определения 1:
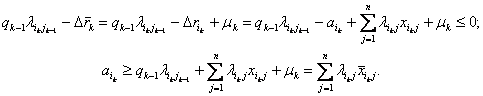
Итак,
условие (2) выполняется для любого узла из множества ![]() , следовательно, оно выполняется для всех узлов
, следовательно, оно выполняется для всех узлов ![]() . Лемма 1 доказана.
. Лемма 1 доказана.
Допустимому
набору узлов ![]() , поставим в соответствие число
, поставим в соответствие число
![]() . (6)
. (6)
Теорема. Для оптимальности решения ![]() задачи (l)-(4) необходимо и достаточно
выполнение неравенства
задачи (l)-(4) необходимо и достаточно
выполнение неравенства
![]() (7)
(7)
для всех допустимых наборов узлов ![]() .
.
Доказательство. Пусть ![]() оптимальное решение
задачи (1)-(4). Докажем, что для любого д.н.у. будет выполняться условие (7).
оптимальное решение
задачи (1)-(4). Докажем, что для любого д.н.у. будет выполняться условие (7).
Допустим, что для
некоторого д.н.у. ![]() условие (7) не
выполняется. Пусть
условие (7) не
выполняется. Пусть ![]() - поток, образованный
после перестановки по этому д.н.у. Тогда, на основании леммы,
- поток, образованный
после перестановки по этому д.н.у. Тогда, на основании леммы, ![]() - допустимое решение
задачи (l)-(4). На основании определения перестановки по д.н.у.
- допустимое решение
задачи (l)-(4). На основании определения перестановки по д.н.у.
![]() ,
,
т.е. решение ![]() не оптимальное, что
противоречит предположению. Необходимость условия (7) доказана.
не оптимальное, что
противоречит предположению. Необходимость условия (7) доказана.
Покажем достаточность
условия (7). Пусть оно выполняется для всех д.н.у. решения ![]() . Покажем, что это решение оптимальное.
. Покажем, что это решение оптимальное.
Предположим противное,
т.е. решение ![]() не оптимальное, и из
него получено решение
не оптимальное, и из
него получено решение ![]() такое, что
такое, что ![]() при помощи действия: поток
при помощи действия: поток ![]() уменьшен, а
поток
уменьшен, а
поток ![]() увеличен на величину
увеличен на величину ![]() . Тогда
. Тогда
![]() . (8)
. (8)
Далее, так как ![]() - допустимое решение
задачи (1) – (4), то выполняются условия
- допустимое решение
задачи (1) – (4), то выполняются условия
 (9)
(9)
для наибольшего порядкового номера
![]() одного и того же
узла во множестве
одного и того же
узла во множестве ![]() , поскольку в противном случае:
, поскольку в противном случае:
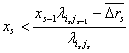
и
![]() ,
,
где
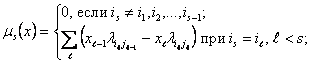
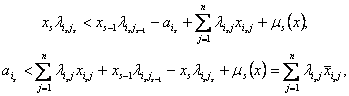
т.е. условие (2) для узла ![]() не выполнено.
не выполнено.
Будет
выполняться и условие
![]() , (10)
, (10)
так как в противном случае:

т.е. условие (2)
не выполнено для узла ![]() .
.
Условия (9) и (10)
совпадают с условиями «а» и «б» в определении. Следовательно, множество ![]() , где
, где ![]() , является допустимым набором узлов. В качестве чисел
, является допустимым набором узлов. В качестве чисел ![]() для этого набора можно принять числа
для этого набора можно принять числа ![]() . Тогда из (8) следует
. Тогда из (8) следует
![]() ,
,
т.е. получили противоречие исходному
предположению. Следовательно, решение ![]() оптимальное. Теорема доказана.
оптимальное. Теорема доказана.
Нетрудно уяснить смысл
выражения (6). Действительно, число ![]() показывает, на сколько
увеличивается
показывает, на сколько
увеличивается ![]() при перестановке
потока по д.н.у.
при перестановке
потока по д.н.у. ![]() .
.
Литература
1. Шанкибаев Б.Н. Целочисленная
распределительная задача //Труды 6-й школы по математическому программированию,
М., 1975, 259-289 с.
2. Шанкибаев Б.Н.
Математическое программирование. Монография. Алматы, «Эверо», 2004, 268 с.