Экономические науки/8. Математические методы в экономике.
Викладач кафедри економіки
підприємства Коваленко О.Ю.
Миколаївський державний гуманітарний університет
імені Петра Могили
Економіко
математична модель визначення оптимальних варіантів розвитку природно-заповідних
територій і об’єктів рекреації по критеріям максимального прибутку при
мінімальних інвестиційних витратах
Сучасні дослідження свідчать, що особливе місце в
системі ефективного управління природно-заповідними територіями належить
інвестиційній діяльності, без належного фінансового забезпечення неможливо
досягти високої ефективності управлінської діяльності [1, c.339-343;
3, c.254-258].
Розглянемо задачу планування розвитку
рекреаційної діяльності та розміщення об’єктів рекреації (санаторії, бази
відпочинку, кемпінги) з оптимальним розподілом інвестиційних ресурсів.
Постановка задачі полягає у наступному. З метою задоволення попиту в
рекреаційних послугах слід забезпечити необхідними об’єктами
зони стаціонарної рекреації навколо природно-заповідних зон.
Для вирішення цієї проблеми до уваги слід взяти усі
можливі варіанти розвитку діючих об’єктів рекреаційної діяльності як в зоні
стаціонарної рекреації (бази відпочинку, готелі, кемпінги тощо), так і в зоні
обмеженої рекреації (туристичні маршрути з відповідною інфраструктурою), а
також наявні проекти введення в дію нових об’єктів. Вибір конкретних варіантів
розвитку та розміщення об’єктів здійснюється з урахуванням обсягів
інвестиційних ресурсів, які можна буде використати для підтримки та підвищення
ефективності їх діяльності. Критерієм оптимальності може слугувати вимога
мінімізації необхідних загальних зведених інвестиційних затрат, максимізації
прибутку від рекреаційних об’єктів в зоні стаціонарної та обмеженої рекреації.
Ефективне управління природно-заповідним фондом передбачає організацію
рекреаційної діяльності зоні регульованої рекреації (Р1) та в зоні стаціонарної
рекреації (Р2). Частина прибутку від цієї діяльності повинна бути направлена на
розвиток заповідників. Ефективне управління повинно визначати оптимальні
варіанти використання потенціалів зон Р1 та Р2, визначити напрями та розміри
інвестицій в рекреаційні зони. для цього розроблена економіко математична
модель оптимального розподілу інвестиційних ресурсів. Ця модель дає можливість
визначити найефективніші варіанти створення нових рекреаційних об’єктів та
експлуатації існуючих. Особливість моделі закладається в поєднанні організації
рекреаційної діяльності в зонах Р1 та Р2. Інша особливість моделі – це
відображення сезонності рекреаційної діяльності. Параметри моделі є істотно
різними для різних сезонів.
Інформаційною основою моделі є база даних рекреаційно-туристичних об’єктів ,
яка містить інформацію про економічні та екологічні параметри об’єктів в
зонах Р1 та Р2. Об’єктами в зоні Р1 є туристично-екскурсійні маршрути, а в зоні
Р2 – санаторії, бази відпочинку, кемпінги та інші рекреаційні об’єкти, як
існуючі, так і запроектовані. До множини об’єктів включаємо і ділянки, на яких
можливе будівництво.
Для кожного об’єкта визначається множина альтернативних варіантів його можливого розвитку. Варіанти
передбачають будівництво нових рекреаційних об’єктів, реконструкцію існуючих,
перепрофілювання об’єктів тощо. Кожний варіант вивчається експертами, які
оцінюють їх економічні, екологічні та інші показники [2].
Експертні дані використовують для підготовки прийняття рішень. Основні етапи проведення експертизи:
1)
визначення
цілі експертизи;
2)
опис об¢єктів оцінювання або їх характеристик на основі бази
даних економіко-екологічного моніторингу;
3)
створення
експертної групи, до якої включаються співробітники заповідників, екологи,
економісти, менеджери рекреаційно-туристичних об’єктів тощо;
4)
визначення
методики експертного оцінювання і способів вираження експертних оцінок;
5)
проведення
експертизи та одержання її результатів;
6)
обробка та
аналіз одержаних результатів експертизи;
7)
повторні тури
експертизи, якщо є необхідність уточнити оцінки експертів або зблизити їх;
8)
Вироблення
варіантів рекомендацій для прийняття рішень на основі одержаної експертної
оцінки.
Як правило, експерти визначають ранги об¢єктів або варіантів. Це означає, що вони вибирають
найкращий за певними показниками варіант, потім другий, третій і т.д. Таке дослідження здійснюється для кожного рекреаційного об’єкта.
В результаті одержуються рангові оцінки.
Основними задачами аналізу рангових оцінок є такі:
1)
визначення
частоти присвоєння варіантам першого рангу;
2)
виявлення
частоти присвоєння варіантам високого рангу;
3)
Визначення зв¢язків між висновками
різних експертів.
Для визначення таких зв¢язків визначаємо коефіцієнт рангової кореляції Спірмена Pij, де i, j - номера експертів.

aik, ajk – ранг к-го варіанту, визначений відповідно i-тим та j-тим експертами, m – загальна кількість варіантів для
даного об’єкту. Близьке до 1
значення цього коефіцієнту означає, що висновки i-того та j-го експертів близькі один до
іншого.
4)
Визначення
коефіцієнта конкордації , якщо показує степінь узгодженості висновків усіх
експертів.
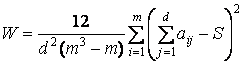
m — кількість варіантів
d — кількість експертів
aij — ранг, який присвоїв j-тий експерт i-му варіанту
s — частка від ділення суми всіх рангів на кількість варіантів
Якщо він близький до 0, то
результати оцінки експертів не узгоджені.
5)
визначення
модальних рангів об¢єктів. Для кожного об¢єкта визначається кількість (1, 2, 3) місць по висновкам експертів.
6)
Визначення
переваги того чи іншого варіанту. Для кожної пари варіантів визначають
кількість експертів, які вважають, що перший варіант кращий другого, і ділимо
цю кількість на загальну кількість можливих варіантів.
7)
Визначаємо
агрегації об¢єктів. Для кожної пари варіантів i, j визначаємо число aij = 1, якщо більшість експертів
вважають кращим i-тий варіант, а якщо j-тий, то aij = 0. Загальний ранг варіанта визначають як кількість
одиниць i-го рядка матриці aij.
8)
Виявлення
лідера серед експертів. Лідером вважається експерт, у якого висновки найближчі
до загальної оцінки. Для кожного
експерта складається матриця індивідуальних переважань. В цій матриці aij=1, якщо даний експерт визнає i-й об¢єкт кращим, ніж j-й. Інші елементи цієї матриці дорівнюють 0. Потім ми порівнюємо матриці
переважань експертів із загальною матрицею переважань і визначаємо кількість
однакових елементів. Той із експертів, для якого ця кількість найбільша і
вважається лідером.
На основі експертних оцінок здійснюється
попередній відбір варіантів розвитку рекреаційно-туристичних об’єктів. На початку видаляються варіанти, які, згідно із
рішенням експертів, в принципі не потрібно реалізувати. Потім для варіантів,
які залишились, визначають показники їх ефективності та роблять ранжування
варіантів за цими показниками. Для
визначення того, наскільки близькими є ранги варіантів за різними показниками,
визначається коефіцієнт конкордації між
показниками і порівнюється із теоретичним значенням. Якщо одержаний коефіцієнт більший від теоретичного значення, то для
реалізації пропонуються варіанти із найвищими рангами. Якщо ж одержаний
коефіцієнт менший від теоретичного
значення, то відбираються варіанти, які по всім показникам, крім одного, мають
високий ранг. При важливості цього показника,
варіант виключається, якщо ж показник не досить важливий, то залишається
для подальшого дослідження. результати експертного оцінювання включаються до бази даних та бази знань в
системі підтримки прийняття рішень.
Подальший вибір варіантів здійснюється
на основі розробленої економіко-математичної моделі.
Розглядаємо параметри моделі
n –
кількість об’єктів в зоні Р2, як існуючих, так і запроектованих.
![]() – кількість можливих
варіантів розвитку для і-того об’єкту. Ці варіанти передбачають будівництво
нових об’єктів, реконструкцію існуючих, перепрофілювання об’єктів тощо. Один із
варіантів передбачає відсутність змін в експлуатації об’єкта.
– кількість можливих
варіантів розвитку для і-того об’єкту. Ці варіанти передбачають будівництво
нових об’єктів, реконструкцію існуючих, перепрофілювання об’єктів тощо. Один із
варіантів передбачає відсутність змін в експлуатації об’єкта.
l – кількість туристичних маршрутів в зоні Р1
Т – кількість сезонів за рік. Сезони визначаються таким чином, щоб протягом одного
сезону параметри рекреаційної діяльності (кількість відпочиваючих, вартість
путівки, графік роботи туристичних маршрутів тощо) істотно не змінювались.
N![]() - максимальна
кількість відпочиваючих на і-тому об’єкті протягом t-го сезону, якщо
даний об’єкт розвивається за j-тим варіантом . Цей параметр залежить від
кількості місць, тривалості путівки та тривалості сезонів.
- максимальна
кількість відпочиваючих на і-тому об’єкті протягом t-го сезону, якщо
даний об’єкт розвивається за j-тим варіантом . Цей параметр залежить від
кількості місць, тривалості путівки та тривалості сезонів.
Iij - інвестиційні затрати для реалізації і-того
варіанта на і-тому об’єкті.
R – максимально можливий обсяг інвестиційних витрат на рекреаційну
діяльність в зоні Р2.
e – коефіцієнт економічної ефективності інвестицій
![]() - прибуток від однієї
людини для i - того об’єкта в t – тий сезон при
розвиткові за j – тим варіантом
- прибуток від однієї
людини для i - того об’єкта в t – тий сезон при
розвиткові за j – тим варіантом
![]() - максимальна кількість людей, які
відвідають r – тий туристичний маршрут в зоні Р1 в t – тий сезон
- максимальна кількість людей, які
відвідають r – тий туристичний маршрут в зоні Р1 в t – тий сезон
![]() - прибуток від
екскурсії за r – тим маршрутом в t – тий сезон,
одержаний від однієї людини з I – того рекреаційного об’єкта
- прибуток від
екскурсії за r – тим маршрутом в t – тий сезон,
одержаний від однієї людини з I – того рекреаційного об’єкта
![]() - кількість
екскурсій, які здійснює людина з I – того
рекреаційного об’єкта в t – тий сезон,
якщо прийнятий j – тий варіант розвитку об’єкта
- кількість
екскурсій, які здійснює людина з I – того
рекреаційного об’єкта в t – тий сезон,
якщо прийнятий j – тий варіант розвитку об’єкта
![]() - коефіцієнт
сезонності, який визначає, наскільки інтенсивно використовується i – тий
рекреаційний об’єкт, що розвивається за j – тим
варіантом в t – тий сезон. Цей параметр визначається
на основі статистичних даних по аналогічним об’єктам або або методом експертних оцінок
- коефіцієнт
сезонності, який визначає, наскільки інтенсивно використовується i – тий
рекреаційний об’єкт, що розвивається за j – тим
варіантом в t – тий сезон. Цей параметр визначається
на основі статистичних даних по аналогічним об’єктам або або методом експертних оцінок
Керованими параметрами є такі
![]() - логічна змінна, що
відображає вибір для реалізації j – того варіанта
розвитку I – того рекреаційного об’єкта
- логічна змінна, що
відображає вибір для реалізації j – того варіанта
розвитку I – того рекреаційного об’єкта
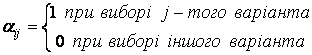
![]() - кількість запропонованих
квитків на екскурсії для I – того об’єкта в t – тий сезон при
розвиткові за j –тим варіантом
- кількість запропонованих
квитків на екскурсії для I – того об’єкта в t – тий сезон при
розвиткові за j –тим варіантом
![]() - кількість екскурсантів, які відвідали r – тий маршрут в t – тий сезон для i – того об’єкта при
розвиткові за j – тим варіантом
- кількість екскурсантів, які відвідали r – тий маршрут в t – тий сезон для i – того об’єкта при
розвиткові за j – тим варіантом
Модель є багатокритеріальною. Перший
критерій – це мінімізація інвестиційних затрат, другий та третій – максимізація
загального прибутку від рекреаційної діяльності в зоні Р1 та в зоні Р2 відповідно. Розглянемо обмеження
моделі
![]()
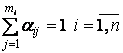 Це обмеження
означає, що для реалізації можна прийняти тільки один варіант для кожного
рекреаційного об’єкта.
Це обмеження
означає, що для реалізації можна прийняти тільки один варіант для кожного
рекреаційного об’єкта.
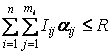 Це обмеження на
загальні кошти для інвестицій в туристично-рекреаційну діяльність.
Це обмеження на
загальні кошти для інвестицій в туристично-рекреаційну діяльність.
![]() Це обмеження
визначає можливі кількості реалізації квитків на екскурсії.
Це обмеження
визначає можливі кількості реалізації квитків на екскурсії.
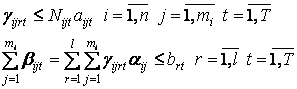 Це обмеження
відображає той факт, що екскурсії здійснюються в зоні Р1 і дають відповідний
прибуток.
Це обмеження
відображає той факт, що екскурсії здійснюються в зоні Р1 і дають відповідний
прибуток.
 Це обмеження відображає
максимально можливі інтенсивності використання маршрутів в зоні Р1
Це обмеження відображає
максимально можливі інтенсивності використання маршрутів в зоні Р1
![]() Це обмеження
потрібно для виключення від’ємних розв’язків
Це обмеження
потрібно для виключення від’ємних розв’язків
Вважаємо три вказані вище критерії
рівноправними, одержимо такий вид цільової функції
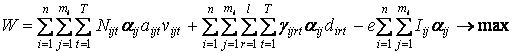
Перший доданок відображає прибуток від
рекреаційної діяльності в зоні Р2, другий – в зоні Р1, третій – зведені
інвестиційні затрати. Розв’язок моделі визначає оптимальні напрямки та розміри
інвестицій та оптимальний розподіл екскурсій між туристичними маршрутами.
Література
1. Стратегічне управління / В.В. Горлачук, В.Г. В’юн, Р.В.
Тарновська, А.Я. Сохнич, В.Д. Чайка / За заг. ред. В.В. Горлачука. – Миколаїв:
Вид-во ПП "Шамрай", 2003. – c.339-343.
2. Дрожжина Л.В., Скалозуб О.О. Математична модель задачі вибору
інноваційних проектів і розподілу капіталовкладень //Збірник наукових праць ДДУ
“Динамічні моделі в економіці” .- 2000.- №3.- с.44-47.
3. Управління землекористуванням / В.В. Горлачук, О.М. Гаркуша, В.Г. В’юн,
В.В. Мельніченко, І.М. Песчанська, Д.М. Демченко / За заг. ред. В.В. Горлачука.
– Миколаїв: Вид-во "ІЛІОН", 2006. – c.254-258.