Сатыбалдиев О. С., Шанкибаев Б.Н.

Республика Казахстан

Центрально-Азиатский университет

Метод сокращения невязок для решения

транспортной задачи

На основании Государственных стандартов образования Республики Казахстан студентам технических специальностей ВУЗов читается курс «Математическое программирование». Раздел «Транспортная задача» является одним из ключевых разделов данного курса. При обучении студентов данному разделу особое внимание уделяется «методу сокращения невязок», далее МСН, опубликованную в работах [1] и [2]. Данный метод является очень эффективным и разница во времени при решении задач транспортного типа между МСН и такими известными методами, как метод потенциалов или венгерский метод, довольно существенна.

Изложим суть МСН на примере классической транспортной задачи: найти наименьшее значение линейной функции

(1)

при ограничениях: (2)

(3)

(4)

Основан алгоритм на следующей теореме оптимальности:

Для того, чтобы решение транспортной задачи было оптимальным, необходимо и достаточно существование для каждой клетки , где , неотрицательной пары чисел и .

Схема алгоритма, состоящего из предварительного и основного этапов, выглядит следующим образом.

Вначале строится матрица , которая не является ещё допустимым планом задачи, так как для него могут быть не выполнены ограничения (2). Для этого псевдоплана строится система из пар чисел и , называемых прямыми и обратными компонентами соответствующей клетки . Затем производится преобразование псевдопланов по схеме до тех пор, пока не будут выполнены все ограничения задачи. При этом, каждый раз, происходит пересчёт компонент и для всех клеток, где изменяется значение .

Как только псевдоплан станет решением системы (2)-(4), он автоматически станет оптимальным решением задачи.

Опишем алгоритм сокращения невязок.

Предварительный этап.

Шаг 1. Все элементы каждого столбца нумеруются в порядке возрастания значений (устанавливаются номера ).

Шаг 2. Во всех клетках устанавливаются значения по формуле

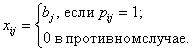(5)

Шаг 3. Для всех клеток устанавливаются прямые компоненты по формуле (6) Здесь клетка столбца , у которой номер на единицу больше номера клетки .

Шаг 4. В клетках с номером устанавливаются обратные компоненты .

Шаг 5. Вычисляются значения

Если все , то задача решена; иначе, выполняется основной этап.

Основной этап.

Шаг 1. Пусть строка, для которой . В строке выбирается наименьшая допустимая компонента (компонента допустимая, если ).

Шаг 2. Пусть на шаг 2 попали по компоненте . Отыскивается строка , для которой имеет место:

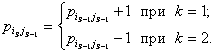(7)

Если , или строка совпадает со строкой , то компонента становится отмеченной и выполняется или шаг 5, если , или шаг 3 по строке . Если , то выполняется шаг 3 по строке .

Шаг 3. Описывается по строке .

В строке отыскивается наименьшая компонента из расширенного множества допустимых компонент, которое образуется добавлением к допустимым компонентам строки ещё одной компоненты . Если она отмеченная, то выполняется шаг 5 при , шаг 4 по строке при . Если компонента неотмеченная, выполняется шаг 2.

Шаг 4. Описывается по строке . Компонента становится отмеченной и вычисляется по формуле

(8)

Выполняется шаг 3 по строке

Шаг 5. Величина уменьшается, а величина увеличивается на

(9)

Здесь строка, удовлетворяющая условию (7).

Шаг 6. В клетке устанавливается компонента по формуле

(10)

Здесь , а - компонента из расширенного множества допустимых компонент. Все компоненты становятся неотмеченными. Выполняется шаг 5 предварительного этапа.

Литература.

1. Шанкибаев Б.Н. Целочисленная распределительная задача //Труды 6-й школы по математическому программированию, М., 1975, 259-289 с.

2. Шанкибаев Б.Н. Математическое программирование. Монография. Алматы, «Эверо», 2004, 268 с.