Доцент Абдрахимова Н.Д.
Академии
управления при Президенте Кыргызской Республики, Кыргызстан
задача ВЫБОРА СУЩЕСТВЕННЫХ ФАКТОРОВ
Проблема определения водопотребления сельскохозяйственных культур в настоящее время является достаточно актуальной, так как Кыргызстан находится в аридной зоне и имеет место дефицит водных ресурсов.
Прогресс в земледелии, а значит и в животноводстве, выражается прежде всего в повышении урожайности и качестве сельскохозяйственных культур, сохранении и приумножении плодородия земель и обеспечении экологически чистого производства. Он достигается оптимизацией технологии и оптимальным удовлетворением потребностей возделываемых растений, рациональным использованием водных ресурсов.
1. Анализ существующих моделей водопотребления
В связи с тем, что определение суммарного водопотребления [1] в практике орошения сопряжено с трудоемкими и длительными полевыми исследованиями, а также возможностью учета и измерения всех действующих факторов, в настоящее время как в странах СНГ, так и за рубежом получили широкое развитие методы, основанные на эмпирической связи водопотребления с метеорологическими показателями, что позволяет без проведения трудоемких опытных исследований, использовать для этих целей данные наблюдений государственной сети гидрометеорологической службы. Так, в практике проектирования оросительных систем в странах СНГ, Болгарии, Чехии и Словакии используется биоклиматический способ, основанный на анализе приходно-расходных элементов водного баланса орошаемой площади. Согласно данному способу суммарное испарение определяют как сумму среднесуточных дефицитов влажности воздуха за расчетный период, помноженных на коэффициент суммарного испарения. Помимо биоклиматического на моделях суммарного испарения основаны методы расчета водопотребления сельскохозяйственных культур, предложенные Шаровым И.А. [2]. Последние позволяют устанавливать водопотребление в зависимости от температурных условий. Для Северного Кавказа суммарное испарение определяют исходя из суммы среднесуточных температур и постоянной расхода воды на один градус [3]. Определение суммарного водопотребления по Алпатьеву А.М. [4] основано на том, что при достаточной влажности верхнего слоя почвы оно приближается к испаряемости. При отсутствии фактических данных об испаряемости, последнюю можно определить, пользуясь формулой Иванова Н.И. [5]. Расчет испарения почвой Тюрком [6] производится на основании данных о температуре, осадках, солнечной радиации, запасах воды в почве, виде растения, возделываемого на орошаемом поле. Максимальное значение декадного испарения зависит от суммарной солнечной радиации. Определение водопотребления Пенманом [7] производится на основе учета солнечной радиации, суточного тепла и испарения с водной поверхности.
На моделях суммарного испарения основаны методы расчета водопотребления сельскохозяйственных культур, предложенные Талалаевским Г.В., Харченко С.И. [8], Данильченко Н.В. [9] и другими. Одни модели более универсальны, другие требуют сложных расчетов, третьи основаны на факторах, не измеряемых на большинстве метеорологических станций. Кроме того, в основном модели ориентированы на определенный регион. Поскольку эти зависимости эмпирические, ошибки при определении водопотребления достаточно велики.
Анализ существующих моделей для определения водопотребления с использованием эмпирических зависимостей показывает, что основными факторами при определении водопотребления являются: испарение, дефицит влажности воздуха, почвы, осадки, скорость ветра, солнечная радиация, продолжительность яркого освещения, атмосферное давление, влажность почвы, температура поверхности земли, а также биологические свойства растений, оказывающие влияние на режим водопотребления. Эти свойства связаны с видом растений, их фазой развития. Все изменения, связанные с различными приемами агротехники, биологическими свойствами растений (селекция, предпосевная обработка семян и т.д.) учитываются через влияние основных факторов. Многофакторная связь испарения с определяющими характеристиками чрезвычайно усложняет исследование режима водопотребления растений. Выявляемые закономерности являются отражением неких существенных сторон или моментов строения или функционирования рассматриваемого объекта моделирования. Прямое установление количественных зависимостей основных факторов, характеризующих внутренние закономерные связи в данных, затруднительно.
Специфические особенности объекта и очень большое количество данных многолетних наблюдений, необходимых для конструирования и идентифицирования модели взаимосвязей, а также требования точности исключают возможность использования традиционных методов. Одним из наиболее эффективных инструментов создания моделей водопотребления является использование одного из классов нового направления в развитии системного анализа - системы Data Mining [10-14], а именно эволюционного программирования, связанного с поиском зависимости целевых переменных от остальных в форме функций какого-то определенного вида. Наиболее удачными алгоритмами этого типа является алгоритмы, применяемые в методе группового учета аргументов (МГУА) [15-20]. Зависимость ищется в форме полиномов.
2. Методы объективного системного анализа
Суть методов этой группы заключается в целенаправленном переборе постепенно усложняющихся структур моделей и их отборе по ряду целесообразных эвристических критериев [10].
Основную ценность имеют сложные многоуровневые алгоритмы самоорганизации. Метод имеет свою область приложения и свои границы применимости. Он зарекомендовал себя работающим методом, об этом свидетельствуют сотни работ. Результатом перебора является модель оптимальной структуры в виде одного уравнения или системы уравнений.
Особенность применения критериев отбора такова, что усложнение структуры модели, повышение ее сложности в начале вызывает уменьшение значения критерия, его стабилизацию, а затем рост.
Наиболее простой из обычно используемых критериев – критерий регулярности. Он применим для моделей, цель которых заключается в прогнозировании. Кроме того, он часто применяется совместно с другими критериями для ликвидации многозначности. При этом его значение вычисляется как среднеквадратическая ошибка на отдельной выборке данных. Среди других критериев следует отметить критерии непротиворечивости и баланса переменных. Они обычно используются для идентификации связей и для долгосрочного прогноза соответственно.
3.
Многорядная модель водопотребления растений
Из рассмотренных выше моделей наилучшей представляется базовая модель с ковариациями
![]() .
.
Данная модель учитывает совместное влияние двух факторов и этим значительно отличается от линейной модели.
Достоинство ее в том, что:
- во-первых, нет катастрофического роста степеней в результирующей модели;
- во-вторых, учитывается не только каждый из факторов в отдельности, но и их взаимное влияние.
Базовая модель является элементом для построения многорядной модели. Последняя может быть представлена в следующем виде
![]() ,
,![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
где ![]() - количество
селектированных моделей;
- количество
селектированных моделей;
![]() - показатель степени сложности модели;
- показатель степени сложности модели;
![]() - свободный член;
- свободный член;
![]() - регрессионный
коэффициент (
- регрессионный
коэффициент (![]() );
);
![]() - модель первой
степени сложности из числа селектированных в первом ряду;
- модель первой
степени сложности из числа селектированных в первом ряду;
![]() - модель
- модель ![]() степени сложности из числа селектированных в
степени сложности из числа селектированных в ![]() ряду
ряду
![]() - модель
- модель ![]() степени сложности из числа выбранных на
степени сложности из числа выбранных на ![]() ряду селекции
ряду селекции
![]() - индексы моделей
предшествующего уровня селекции, включаемые в данную модель.
- индексы моделей
предшествующего уровня селекции, включаемые в данную модель.
В качестве критерия для построения модели выбран критерий регулярности - минимум среднеквадратической ошибки на отдельной проверочной последовательности.
4. Алгоритмы объективного системного анализа
Алгоритмы делятся на комбинаторные и многорядные. В комбинаторных заранее задается некоторая модель наивысшей сложности и на оптимум проверяются различные подмодели.
В многорядных (пороговых алгоритмах) процесс построения модели расчленяется на несколько рядов селекции. Каждому ряду соответствует определенная степень сложности модели. Из множества возможных моделей отбираются по заданному критерию лучшие для использования в следующем ряду. Ряды селекции наращиваются до тех пор, пока значение критериальной функции имеет тенденцию к уменьшению.
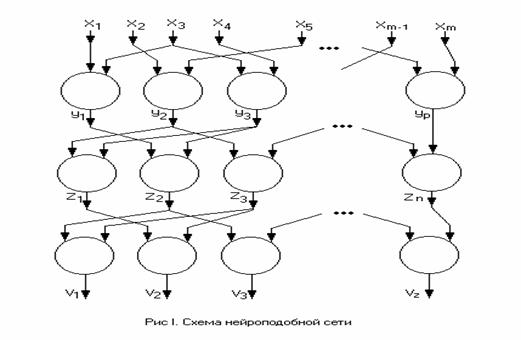
Организация поиска единственной модели оптимальной сложности может быть также реализована при помощи многорядного алгоритма, где вместо пороговых самоотборов на каждом ряду селекции осуществляется приравнивание нулю коэффициентов некоторого полинома. Из ряда в ряд пропускаются все переменные без пороговых самоотборов. Получаемая при этом структура напоминает нейронную сеть.
В рассматриваемой задаче использовалась сеть вида, представленного на рис. 1. Полный перебор можно заменить поиском оптимальных значений в пространстве коэффициентов.
5. Методика анализа состава факторов модели
водопотребления
Анализ совместного влияния факторов на результирующий показатель проводится рассмотрением совместного влияния каждой пары факторов на результирующий показатель. На первом шаге было выбрано фиксированное число пар факторов, которые давали наилучшее значение критерия отбора. На втором шаге отбирались парные комбинации из полученного списка, которые также давали наилучшее значение критерия. Процедура повторялась до тех пор, пока значения критерия приближались к оптимуму.
Основные характеристики примененного метода представлены ниже.
Исходные данные разбиваются на два подмножества (обучающая и проверочная последовательности).
Один из наиболее простых вариантов заключается в следующем способе формирования последовательности
![]() ,
,
где ![]() - обучающая
последовательность;
- обучающая
последовательность;
![]() - отдельное наблюдение;
- отдельное наблюдение;
![]() - количество
наблюдений;
- количество
наблюдений;
\ - целочисленное деление.
![]() ,
,
где ![]() - проверочная
последовательность.
- проверочная
последовательность.
Связи анализировались в классе полиномиальных частных моделей второго порядка без квадратичных членов
![]() .
.
В качестве критерия использовалась зависимость, по смыслу соответствующая критерию регулярности: минимум суммы квадратов отклонений на данных проверочной совокупности
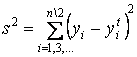 ,
,
где ![]() - критериальное значение;
- критериальное значение;
![]() - наблюдаемое значение
зависимой переменной;
- наблюдаемое значение
зависимой переменной;
![]() - теоретическое
значение, вычисленное по модели, построенной на основе обучающей совокупности.
- теоретическое
значение, вычисленное по модели, построенной на основе обучающей совокупности.
Необходимо отметить, что выбранный способ формирования совокупности наблюдений применим в тех случаях, когда в исходных данных отсутствуют периодические составляющие высоких порядков. Данные наблюдений, использованных при построении модели водопотребления, удовлетворяют этому условию.
6. Компьютерная
реализация системы извлечения знаний
Метод выделения существенных факторов реализуется в два прохода. На первом проходе путем анализа совместного влияния пар факторов строятся списки наиболее существенных из них. Это соответствует построению некоторой подсети полной сети всех возможных комбинаций факторов. На каждом из уровней сети остается много висячих вершин, которые связаны с исходными факторами, но не соединены с вершинами, соответствующими оптимальным комбинациям. Для достижения поставленных целей необходимо выполнение и второго прохода. На втором проходе (обратный ход) – анализ проводился "снизу" от оптимальных комбинаций к исходным факторам. При этом отбрасывались все висячие вершины – тупиковые участки сети.
В результате выполнения второго прохода получаем список исходных показателей, вошедших в выбранные оптимальные комбинации (рис.2)
|
|
Внешний критерий |
||||
|
|
|
|
|||
|
Конструирование моделей |
|||||
|
|
|
|
|||
|
Совокупность подмоделей |
|||||
|
|
|
||||
|
Выбор факторов, вошедших в оптимальную модель |
|||||
|
|
|
||||
|
Отчет о составе существенных факторов |
|||||
|
Рис.2. Модель водопотребления |
|||||
Программа написана на языке Фортран для эксплуатации в пакетном режиме. Формат представления исходных данных и результатов будет ясен из примера, приведенного в разделе 7.
7. Состав существенных факторов, необходимых для прогнозирования водопотребления люцерны
Для анализа были взяты общедоступные данные УГМС Кыргызстана: дата, начальная влажность в слое, количество дней от укоса, солнечная активность, температура воздуха, температура поверхности почвы, относительная влажность, дефицит насыщения, атмосферное давление, скорость ветра, сумма осадков за сутки. Расчеты проводились многократно в различных вариантах. Удовлетворительные результаты получены при следующих характеристиках процесса:
- количество рядов селекции – 12;
- количество комбинаций, отбираемых на каждом ряду селекции – 12;
- количество факторов на каждой частной комбинации – 2;
- монотонность снижения до 11 ряда и стабилизация на 12.
После отбора остались следующие исходные факторы: дата, начальная влажность в слое, солнечная активность, температура воздуха, относительная влажность, атмосферное давление, скорость ветра, сумма осадков за сутки.
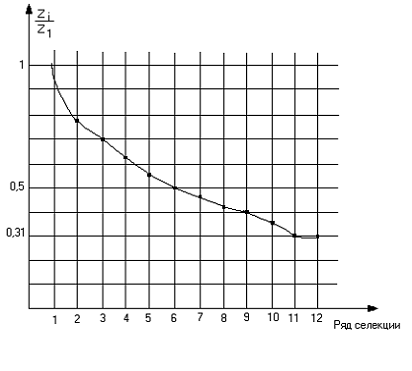
В процессе анализа были исключены следующие факторы: количество дней от укоса,
солнечная активность, температура поверхности почвы, дефицит насыщения. Характер
изменения внешнего критерия иллюстрируется на рис.3.
Рис. 3.
Характеристика изменения внешнего критерия
![]() - значение критерия в
первом ряду,
- значение критерия в
первом ряду,
![]() - значение критерия в
ряду
- значение критерия в
ряду ![]() .
.
8. Модель водопотребления люцерны
Всего получено двенадцать моделей примерно одинакового качества. Каждая из моделей предполагает выполнение вычислений на шести уровнях. Результаты представляются в виде таблиц (см. табл.1), которые имеют одинаковую структуру и содержат:
- номер переменной – номер модели;
- номер члена – порядковый номер члена в рассматриваемой модели;
- коэффициенты (параметры) модели;
- 1, …, 12 – номера переменных (моделей) следующего уровня, входящих в рассматриваемую модель (переменную).
Таблица 1
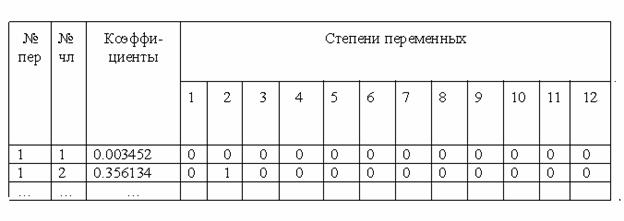
Характеристики модели водопотребления
В табличной части показаны степени, с которыми входят указанные переменные в состав следующего члена модели. Например, в первой строке таблицы 1 содержится информация о том, что в первую модель входит член (первый) с коэффициентом 0,003452 и все переменные следующего уровня с нулевыми показателями степеней. Во второй строке – второй член с коэффициентом 0,356134 с нулевыми показателями степеней всех переменных за исключением второй, имеющей показатель степени, равный единице.
Исходные
переменные первой таблицы вычисляются с
помощью таблицы 2, второй – с помощью таблицы 3 и так далее до исходных переменных таблицы 6. Последние
являются существенными факторами водопотребления люцерны. Порядок расчетов с
помощью таблиц одинаков на всех уровнях и аналогичен, описанному в таблице 1.
Заключение. В процессе выполнения исследований получены следующие результаты:
1. Разработана методика анализа существенных факторов модели водопотребления на основе метода группового учета аргументов.
2. Определен состав существенных факторов, необходимых для прогнозирования водопотребления люцерны.
3. Разработана модель водопотребления люцерны.
Литература:
1. Костяков А.Н. Основы мелиорации – М.: Сельхозгиз, 1960.
2. Шаров И.А. Эксплуатация гидромелиоративных систем - М.: Сельхозгиз, 1959.
3. Льгов Г.К. Орошаемое земледелие Северного Кавказа – Ордженикидзе: Кн. издат Северной Осетии, 1967.
4. Алпатьев А.М. Влагооборот культурных растений – Л.:Гидрометиздат, 1954.
5. Иванов Н.И. Об определении величины испаряемости/Известия ВГО, т.26, вып.2. –1954.
6.
Turc,
L. Evaluation des besoinsen eau d'irrigation evapotranspiration potentille. –
Ann. Agror., Paris, 12(1961), p13-49.
7.
Penman
H.L. Natural Evaporation from Open Water, Bare Soil and Grass. – Proc. Roy.
Soc. London, 1948, A193; 120-146.
8. Харченко С.И. Гидрология орошаемых земель – Л.:Гидрометиздат, 1976.
9. Данильченко Н.В., Попыркин А.Н. Временные технические указания по расчету поливных режимов основных сельскохозяйственных культур, зернового и кормового севооборота в условиях Казахстана./Каз. НИИВХ – Джамбул, 1972.
10. Ивахненко А.Г. Долгосрочное прогнозирование и управление сложными системами – Киев: Технiка, 1975. 312c
11. Дюк В.А., Самойленко А.П Data Mining: учебный курс СПб.: Питер, 2001
12. Brand E., Gerritsen R Data Mining
and Knowledge Discovery DBMS. 1998. №7
13. Parsaye KA Characterization of Data Mining Technologies and Processes The Journal of Data Warehousing. 1998.№ 1
14. Киселев М., Соломатин Е Средства добычи знаний в бизнесе и финансах Открытые системы. 1997. № 4. С. 41-44
15. Эделстейн Г Интеллектуальные средства анализа, интерпретации и представления данных в информационных хранилищах ComputerWeek-Москва. 1996. № 16. С. 32-33
16. Ивахненко А.Г. Индуктивный метод самоорганизации моделей сложных систем. Киев, Наукова думка, 1981.-296c.
17. Ивахненко
А.Г., Мюллер Й.А. Самоорганизация прогнозирующих моделей. Киев: Технiка, 1985;
Berlin: Verlag Technik, 1984, 223 с.
18. Ивахненко А.Г., Степашко В.С. Помехоустойчивость моделирования - Киев: Наук. думка, 1985. - 216 с.
19. Обнаружение закономерностей
взаимодействия ионов с поверхностью материалов по Комбинаторному алгоритму МГУАFarlow, S. J. (ed.).
Self-organizing Method in
Modeling: GMDH Type Algorithms. Statistics: Textbooks and Monographs, 54,
1984.
20. Madala, H.R., and Ivakhnenko, A.G.
Inductive Learning Algorithms for Complex Systems Modeling. Boca Raton, CRC
Press Inc., 1994.