Математика/3. Теория вероятностей и математическая статистика

 

К. ф.-м.н. Бураковский В.В.

Гомельский государственный университет им. Ф.Скорины, Беларусь

Симметричная КЛВС с бесконечными

буферами и вентильным обслуживанием

 

Рассмотрим симметричную кольцевую маркерную ЛВС, объединяющую N абонентских станций, каждая из которых имеет бесконечный буфер. Будем исследовать случай ветнильной дисциплины обслуживания на АС, когда после получения маркера станция передает все данные, накопившиеся у нее за время цикла Т. На каждую АС поступает пуассоновский поток сообщений с одинаковой интенсивностью . Причем данные поступают пачками так, что данные одного поступления с ве­роятностью  упаковываются в - пакетов, . За один цикл дли­тельности Т (интервал времени между последовательными поступле­ниями маркера на одну АС) на каждую АС поступит случайное число сообщений, которые упаковываются в  пакетов. При этом случайные величины  независимы в совокупности.

Обозначим через  время передачи сообщения между соседними АС, а - время приема сообщения на АС - адресате,  - число паке­тов, имеющихся на некоторой АС в момент поступления -гo CM, -число пакетов, поступивших на эту АС в течение -гo цикла. Тогда имеет место рекуррентная формула

                                                 (1)

Основными характеристиками, определяющими эффективность функционирования рассматриваемой КЛВС, являются следующие: 

1) среднее время задержки пакета на АС ;

2) коэффициент загрузки АС ;

3) коэффициент загрузки моноканала К;

4) пропускная способность КЛВС П;

5) условие существования стационарного режима.

Теорема. Характеристики 1-5 рассматриваемой КЛВС определяются по формулам:

                                                         (2)

                                                  (3)

                                                           (4)

                                                           (5)

                                                           (6)

где  

Доказательство. По формуле полной вероятности, учитывая (1), получим

                                     (7)

В стационарном режиме  не зависят от . Обозначим для стационарного режима . Тогда получим для  систему уравнений

                                                (8)

Здесь через  обозначена безусловная вероятность поступления и пакетов на АС за один цикл, которая вычисляется по формуле

где F(T) - функция распределения длительности цикла, а интегриро­вание производится по всему интервалу возможных значений T, q'(T)– условная вероятность поступления и пакетов за один цикл, если он продолжался время Т. В нашем случае , где п – число со­общений, переданных за один цикл, . Таким образом, F(T) яв­ляется дискретным распределением. Обозначая через – вероят­ность того, что за один цикл передано п сообщений, получим

Обозначим производящую функцию числа пакетов, необходимых для передачи данных, поступивших в одной пачке

Тогда производящая функция числа пакетов, необходимых для переда­чи данных, поступивших за время Т на одну АС, имеет вид

Поскольку все АС одинаковые, то производящая функция числа паке­тов в КЛВС за один цикл равна

                                               (9)

Отсюда следует, что среднее число пакетов, передаваемых за цикл длительности Т

                                           (10)

Поскольку средняя длительность цикла равна , получаем следу­ющее уравнение для определения явного вида

Откуда

                                                       (11)

где 

Таким образом, условие существования стационарного режима в КЛВС  имеет вид (6).

Среднее значение длительности цикла

                                            (12)

Поскольку в рассматриваемом варианте дисциплины обслуживания передаются все данные, имеющиеся на АС к моменту прихода СМ, то среднее число переданных за цикл пакетов соответствует среднему числу имеющихся пакетов данных в КЛВС. Так как все АС имеют оди­наковые характеристики, то среднее число пакетов данных на одной АС

                                             (13)

Рассматривая каждую АС как СМО типа , по формуле Литтла получаем, что среднее время пребывания пакета в КЛВС, то есть среднее время задержки, определяется соотношением

                                                       (14)

следовательно в рассматриваемом случае совпадает со средней дли­тельностью цикла.

Коэффициент загрузки АС . Поскольку , то  вычисляется по формуле (3),

Коэффициент загрузки моноканала передачи полезной информации вычисляется как отношение среднего времени, которое передается информация с АС, к средней длительности цикла

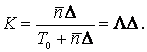
Пропускная способность КЛВС

Теорема доказана.

Очевидно, что в рассматриваемом случае среднее время задержки сообщений монотонно увеличивается с ростом . Поэтому условная пропускная способность КЛВС  при условии, что  находится из уравнения

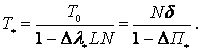                                         (15)

Откуда

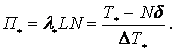                                             (16)

Рас­четы, проведенные на ПЭВМ, дают возможность построить гра­фики зависимостей коэффициентов загрузки АС, коэффициентов загрузки моноканала, средних времен задержки сообщений на АС от сум­марной интенсивности  поступления пакетов в КЛВС для обеих дис­циплин обслуживания.

 

ЛИТЕРАТУРА

 

1.                        ANSI/IEEE 802.5 Standard – 1985. Token-passing ring access method and physical layer specification // IEEE Press, 1985, 89p.

2.                        Бураковский В.В., Медведев Г.А. Кольцевая локальная сеть с протоколом маркерного доступа // Техника средств связи. Сер. Системы связи, М., 1990, Вып. 7. с. 9-16.

3.                        Бураковский В.В. Кольцевая локальная сеть с протоколом маркерного доступа, буферами конечной ёмкости и вентильной дисциплиной обслуживания. ГГУ, Гомель, 1997. 9с. Деп. в БелИСА 12.06.1997 г., №Д199716.

4.                        Бураковский В.В. Исследование кольцевых маркерных локальных вычислительных сетей при помощи циклических марковских процессов. Препринт №31 Гомель, ГГУ, 1997. 15с.