А.П.Мустафаев
Семипалатинский государственный университет имени Шакарима
Связь между решениями линейных
уравнений в частных производных разного порядка гиперболического типа
Многие задачи физики
приводят к разысканию той или иной функции нескольких переменных. Для её
определения составляется дифференциальное уравнение в частных производных,
которому должны удовлетворять искомая функция.
Наряду с общими методами,
применяемыми при решении уравнений с частными производными, существуют для
каждого типа уравнений и некоторые специфические методы.
В этой работе покажем
последовательную взаимосвязь частных видов общих решений некоторых линейных
уравнений с постоянными коэффициентами различного порядка гиперболического
типа.
Рассмотрим несколько
уравнений гиперболического типа:
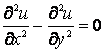 (1)
(1)
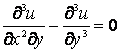 (2)
(2)
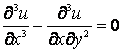 (3)
(3)
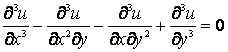 (4)
(4)
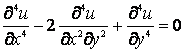 (5)
(5)
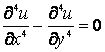 (6)
(6)
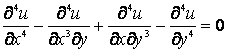 (7)
(7)
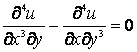 (8)
(8)
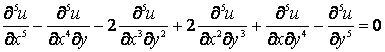 (9)
(9)
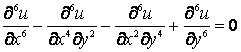 (10)
(10)
Все эти уравнения
получены из уравнения колебания струны (1) взятием от него частных производных
различного порядка по одной или по двум переменным.
С помощью замены
![]() (*)
(*)
уравнение (1) приводится к
дифференциальному уравнению вида
![]() (1.1)
(1.1)
а уравнения (2)-(4)
![]() (2.1-4.1)
(2.1-4.1)
а уравнение (5)
![]() (5.1)
(5.1)
а уравнения (6)-(8)
![]() (6.1-8.1)
(6.1-8.1)
а уравнение (9)
![]() (9.1)
(9.1)
а уравнение (10)
![]() . (10.1)
. (10.1)
А общие решения этих
уравнений соответственно имеют вид
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() производные
постоянные. Перехода к старым переменным х и у, получим общие решения соответствующих уравнений с постоянными
коэффициентами гиперболического типа в явном виде.
производные
постоянные. Перехода к старым переменным х и у, получим общие решения соответствующих уравнений с постоянными
коэффициентами гиперболического типа в явном виде.
Непосредственной
проверкой можно убедиться, что эти решения удовлетворяют соответственным
уравнениям, а также легко можно заменить связь решений уравнений высших
порядков с уравнениями низших порядков.