Дракунов Ю.М., Молдыбаева А.А.

Республика Казахстан

Казахский Национальный университет им. Аль-Фараби

Решение дифференциального уравнения движения машинного агрегата с одной степенью свободы в классе обобщенных функций

Пусть задана некоторая функция и известны значения этой функции в точках и число разбиений. Тогда интеграл этой функции можно аппроксимировать ступенчатой функцией, которая может быть записана через обобщенные функции [1]

(1)

Здесь представляет собой обобщенную функцию Хевисайда, а соответствующие слагаемые – площади прямоугольников (первое слагаемое – это площадь начального прямоугольника). Если принять , то первое слагаемое в формуле (1) можно занести под знак суммы

(2)

Обычно в задачах механики полагают в качестве начального значения времени или соответствующего граничного условия. Нетрудно также записать выражение для интеграла функции

(3)

Так как в классе обобщенных функций определена функция Дирака как производная от функции Хевисайда , то дифференцируя (2) получим выражение для нашей функции

(4)

Часто приходится иметь дело со значениями рассмотренных функций в узловых точках, поэтому для значений можно записать

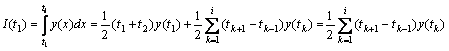(5)

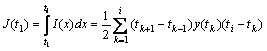(6)

Уравнение движения машинного агрегата с одной степенью свободы может быть записано в виде

(7)

Здесь - приведенный момент инерции и его производная по обобщенной координате , а - приведенный момент движущих сил и сил сопротивления.

С учетом начальных условий, при , первый интеграл дифференциального уравнения (7) можно записать

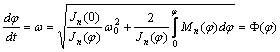(8)

В силу периодичности движения интервал [0,2] разбиваем на частей. Тогда можно определить значения функции в узловых точках

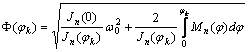. (9)

В случае разрывной или сложной функции для приведенного момента интеграл в подкоренном выражении можно вычислить через обобщенные функции

(10)

Аппроксимируем дифференциальное уравнение с помощью обобщенных функций Дирака согласно выражению (4)

, (11)

Приближенное решение этого уравнения может быть записано через обобщенные функции Хевисайда

, (12)

Рассмотрим иной подход к решению дифференциального уравнения (7). Для этого представим его в виде системы уравнений первого порядка

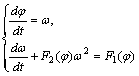
Где , .

Решение этих уравнений запишем через обобщенные функции

,

, .

Таким образом, относительно и , мы приходим к системе нелинейных уравнений, которая может быть решена методом итераций.

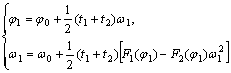
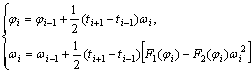
Здесь . Из этих систем можно выразить через :

.

Список литературы:

1. Кеч В., Туодореску П. Введение в теорию обобщенных функций с приложениями в технике. М., Мир,1978, 519 с.

2. Хайрер Э., Нерстетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М., Мир,1990, 513с.

3. Тюреходжаев А. Н. Некоторые проблемы современной инженерной практики. Материалы международной научной конференций «Актуальные проблемы механики в машиностроении», т.1,Алматы, 2005,с,11-28.

4. Теория механизмов и механика машин: Под ред. К.В. Фролова М.: Высшая школа,2003, 496 с.