Артюхин Антон Владимирович

г. Алматы АО «КазИнж Электроникс»

 

Математическая модель определения вероятности  облучения при работе с источниками радиоизлучения

 

 

       Телекоммуникационные предприятия, работающие с источниками радиоизлучения различной мощности, относятся к объектам с повышенной опасностью и отличаются тем, что наличие фонового излучения, особенно в ближней зоне, может быть незаметно. При этом, электромагнитные поля человек не видит и не чувствует и именно поэтому не всегда предостерегается от опасного воздействия этих полей, следовательно вредное воздействие излучения на обслуживающий персонал не так очевидно, но не становится от этого менее опасным. При определении реальных причин возникновения несанкционированного фонового излучения приходится учитывать довольно большое количество параметров, в том числе неудовлетворительную организацию работы, нарушения трудовой и технологической дисциплины, отказ или частичную неработоспособность эквивалентов нагрузки, нарушения условий для получения требуемой диаграммы направленности, отсутствие или отказ автоматизированного контроля коэффициента стоячей волны в фидере. Наличие нескольких одновременно излучающих источников с различными несущими частотами еще больше усугубляет данную проблему.  Поэтому, при определении вероятности облучения, как степени риска возникновения нежелательного события, необходимо рассматривать весь процесс как сумму  определенных составляющих. Целью данной работы является попытка создания математической модели для определения степени риска облучения производственного персонала ЭМП на основе автоматизированной системы контроля электромагнитной обстановки на рабочих местах предприятий телекоммуникаций.

          Первой составляющей является детерминированный процесс, вызванный возникновением внеполосных излучений и побочных излучений, связанный с техническим состоянием передающего радиоцентра либо базовой станции сотовых или транкинговых систем связи. Причины возникновения внеполосных излучений и побочных излучений общеизвестны, при этом за уровнем этих излучений контроль ведет специальная служба. Второй составляющей является вероятностный  процесс, который может быть вызван неудовлетворительной организацией работы, нарушением трудовой и технологической дисциплины, изменением условий работы или другой причиной. И, наконец, третья составляющая – это чисто случайный процесс, принципиально непредсказуемый, который  может быть вызван, например, отказом автоматизированной системы контроля или возникновением внештатной ситуации, или некачественным электропитанием либо его отключением.

        Детерминированные процессы можно рассчитать заранее с достаточно высокой точностью [1]. Закон управления процессом работы радиопередающего центра может быть выражен в виде таблиц, графиков или аналитической функции. Учитывая периодичность изменения нагрузки, логично остановиться на гармонической функции. Функция x(t) не имеет бесконечно больших ординат и характеризуется конечным числом точек излома в интервале (a < t < b). Если принять длину периода равную (b - a), то для функции x(t) будет справедливо разложение Фурье:

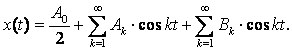                                        (1)

           Коэффициенты Аk и Вk определяются в виде:

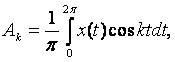
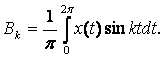                                              (2)

        Определив период функции x(t) необходимо отыскать значения коэффициентов Аk и Вk. При решении задач интерполирования или экстраполирования могут быть использованы средства вычислительной техники.

         Вероятностные процессы могут быть описаны с помощью статистической теории предсказаний [2]. Даже при наличии накопленного опыта, точное предсказание невозможно по многим причинам, прежде всего потому, что не все причинные факторы, участвующие в процессе, достаточно известны. Поэтому описать или предсказать будущие события можно лишь приближенно. Для рассматриваемого случая целесообразно применить теорию стационарных случайных процессов, когда результат зависит не от одной случайной величины, а от двух или более. При этом считаем, что случайная величина Y независима от случайной величины X, то есть закон распределения величины Y не зависит от того, какое значение приняла случайная величина X. Для непрерывных случайных величин, каковыми являются изменение диаграммы направленности антенны или изменение выходной мощности передатчика, основными числовыми характеристиками будут математическое ожидание и дисперсия:

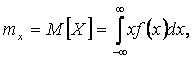
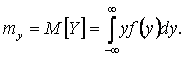                                           (3)

                                                    (4)

         В случае, если будет установлена статистическая связь между изменением диаграммы направленности антенны и изменением выходной мощности передатчика, помимо математического ожидания и дисперсии случайных величин необходимо будет учитывать корреляционный момент:

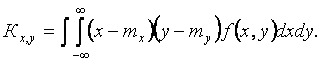                                                           (5)

         Для определения критерия качества прогнозирования можно выбрать математическое ожидание квадрата ошибки:

                                         (6)

          где прогнозируемые функции; действительные функции;  ошибки прогнозирования.

          Так как прогнозируемые функции представляют собой сумму регулярных составляющих и случайных стационарных составляющих, то можно сформулировать критерий оптимальности. Считаем, что математическое ожидание и дисперсия полностью определяют закон распределения ошибки. Критерий максимума вероятности того, что ошибка прогнозирования будет изменяться в заданных пределах:

                                              (7)

         где заданная функция.

         Интегральная квадратичная ошибка будет:

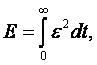                                                                                                             (8)

         где; регулярная составляющая прогнозируемой функции.

         Прогнозируемая функция записывается в виде:

                                                                         (9)

         где дисперсия случайной составляющей.

         Прогнозирование будет оптимальным, если обеспечиваются минимум суммы с весом а интегральной квадратичной ошибки (8) и с весом с дисперсии случайной ошибки при удовлетворении условия:

                                                                                             (10)

          Для  чисто случайных, принципиально непредсказуемых, процессов имеет значение не величина ошибки, а лишь качественный факт наличия или отсутствия ошибки. В таком случае приходится пользоваться критерием минимума вероятности ошибочного решения [3]:

                                                          (11)

          Наличие ошибочного решения будет в случае, если его оценка Х* превышает некоторый порог с, и что ошибочного решения нет, если Х*<c. Условный минимум вероятности ошибочного решения при заданной условной вероятности ложного обнаружения признака известен под названием критерия Неймана – Пирсона. При этом, критерий (11) можно представить как критерий минимума математического ожидания такой функции  l(X,X*) процесса и его оценки, которая равна нулю при правильном распознавании, т.е. когда Х=0, Х*≤C или Х*>C, X≠0, и равна единице при ошибочном распознавании, т.е. когда Х≠0, Х*≤C или Х*>C, X=0:

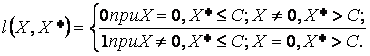                                     (12)

         Математическое ожидание функции l(X,X*) можно выразить как:

                                         (13)

         Таким образом, критерий минимума вероятности ошибочного решения (11):

                                                                              (14)

          Качество принятого решения оценивается функцией l(X,X*), т.е. определено конкретной (действительной) реализацией Х и прогнозируемого значения Х*. При всех возможных реализациях прогнозируемых значений и  действительной реализацией качество решения определяется условным риском, а именно математическим ожиданием функции потерь:

                                 .                                          (15)

         Качество всех принятых решений при всех возможных реализациях действительных значений Х и прогнозируемых значений Х* характеризуется математическим ожиданием условного риска или средним риском:

                                                           (16)

          Таким образом, в качестве критерия оптимальности принимается критерий минимума среднего риска в форме (14). При наложении дополнительных условий:

                                             (17)

задача значительно усложняется, но решение можно обеспечить, применяя метод неопределенных множителей Лагранжа. Потребуется отыскать минимум величины:

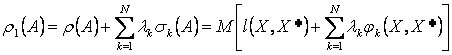               (18)

         Эта величина  может рассматриваться как средний риск, соответствующий функции потерь:

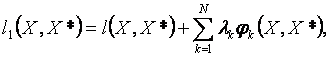                                          (19)

зависящей от множителей λ1,   …,  λN.

         Сравнительный анализ составляющих процесса несанкционированного излучения ЭМП в окружающую среду радиопередатчиком позволяет сделать следующие выводы:

          - наиболее предсказуемыми и рассчитанными заранее с достаточно высокой точностью являются детерминированные процессы, вызванные периодическими изменениями нагрузки, наименее предсказуемыми являются чисто случайные процессы, принципиально непредсказуемые, связанные с нарушением технологической дисциплины, отказом техники,  некачественным электроснабжением или другими случайными причинами;

          - для увеличения точности прогнозирования и повышения качества определения степени риска загрязнения окружающей среды необходима разработка программного обеспечения, учитывающего все составляющие несанкционированных излучений ЭМП и позволяющего с высокой степенью вероятности предсказывать возможные загрязнения;

          - вне зависимости от существующих систем контроля необходима независимая автоматизированная система оперативного учета уровня вредных  ЭМП, превышающих ПДУ, позволяющая принимать адекватные меры по снижению уровня ЭМП и степени риска облучения производственного персонала и, как следствие,  способствующая улучшению экологической обстановки.

            Литература

          1. А.Г. Ивахненко, В.Г. Лапа. Предсказание случайных процессов. – Киев.: Наукова думка, 1971.

           2. Гренандер У. Случайные процессы и статистические выводы. – М.: ИЛ, 1961.

           3. Основы автоматического управления. – Сб. под ред. В. С. Пугачева. – М.: Физматгиз, 1963.