Карачун В.В., Мельник В.М.

Національний технічний університет України «КПІ»

Обчислення перехідного процесу збуреного стану струни за неявною схемою

Відомий факт, що явна схема, яка розглянута в процедурі Stept, є стійкою за умови

. (1)

Цю умову можна задовольняти, вибираючи достатньо малий крок (коли і відомі). За необхідності реалізації кроку , більшого, ніж дозволяється нерівністю (1), можна вдатися до так званої неявної схеми.

Добру неявну схему можна одержати заміною в диференціальному рівнянні похідних різницевими співвідношеннями -

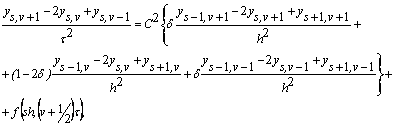(2)

де - умова стійкості неявної схеми.

Для зручності подальших перетворень, наведемо (2) у вигляді -

; ,_, (3)

де

Залежності (3) утворюють систему з (m-1) рівнянь відносно (m+1) невідомих, ., _. Якщо цю систему доповнити двома граничними умовами, то вона може бути розв’язана відносно невідомих . Подібну систему раціонально розв’язувати методом прогонки, який, по суті, реалізує схему Гауса послідовного виключення невідомих. У процесі виконання прямого ходу в методі прогонки зведемо рівняння (3) до вигляду -

, (4)

Щоб знайти рекурентні формули для обчислення і , досить підставити (4) в (3) замість. Отримуємо -

, .

Після зведення подібних і ділення на коефіцієнт при маємо

. (5)

Порівняння (4) і (5) виявляє, що -

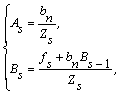(6)

де .

Формули (6) спрацьовують за умови, коли визначені та граничними умовами на лівому кінці струни (якщо ).

При граничній умові I роду при , бачимо, що

(7)

Гранична умова II роду при дає аналогічно

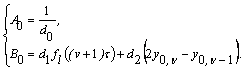(8)

Це справедливо, якщо маса в момент, що розглядається, не знаходиться в точці . Інакше -

(9)

За граничної умови III роду отримуємо (при відсутності маси в точці ):

(10)

Якщо ж маса знаходиться на лівому кінці, тоді маємо -

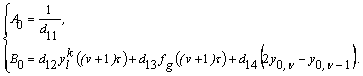
Визначивши та , можна починати прямий хід, тобто послідовно обчислювати , ,, і так далі, поки не буде досягнута точка _, де , за умови, що .

Для вузла повинна виконуватися вимога -

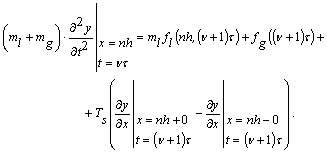(11)

У дискретних змінних -

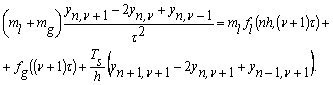
Замінимо в останньому співвідношенні його значенням, обчисленим через (4) -

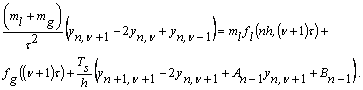
Зведемо подібні:

Розділимо на квадратну дужку -

, (12)

де ; ;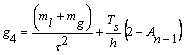

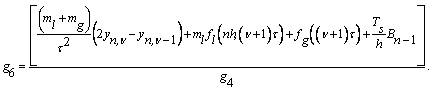
Порівнюючи (12) із (4), робимо висновок, що

(13)

Після обслуговування вузла прямий хід продовжується за формулами (6), як звичайно, аж до значень .

Завершуючи прямий хід, визначимо, стикуючи останній крок прямого ходу, тобто -

(14)

з відповідною граничною умовою на правому кінці (при ).

При граничній умові I роду

, (15)

і додаткове стикування не потрібно.

За граничної умови II роду і відсутності маси в точці , одержуємо:

Порівнюючи останній вираз з (14), доходимо висновку -

звідки

(16)

При знаходженні маси в точці маємо -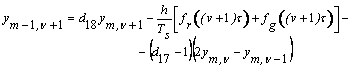

Зіставляємо останній вираз з (14), бачимо -

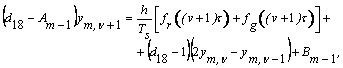
звідки

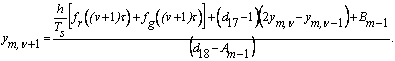(17)

При граничній умові III роду і відсутності маси в точці , отримуємо –

Порівнюємо цей вираз з (14) :

звідкіля маємо -

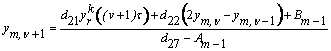. (18)

І, нарешті, при знаходженні маси в точці , з маємо:

Зіставляємо останній вираз з (14) -

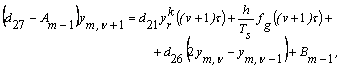
звідкіля -

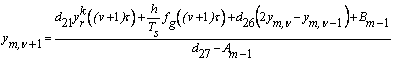. (19)

Співвідношення (6)…(19) покладені в основу підпрограми StepN, що реалізує крок за часом для неявної схеми.

Procedure StepN;

Var s:integer;

А, В, Y:CoefR; FS, ZS:real;

Begin

Т:= Т+Tau; n:=round(Xg(Т)/Hx);

case Ngl of

1: begin А[0]:=0; В[0]:=Yl(Т) End;

2: if n<>0 then

begin

А[0]:=1/D0;

В[0]:=D1*Fl(Т)+D2*(2*Yt[0]-Yp[0])

end

else

begin

А[0]:=1/D3;

В[0]:=D4*(Fl(Т)+Fg(Т))+D5*(2* *Yt[0]-Yp[0])

end;

3: if n<>0 then

begin

А[0]:=1/D7; В[0]:=D8*Ylk(Т)+

D9*(2*Yt[0]-Yp[0])

end

else

begin

А[0]:=1/D11; В[0]:=D12*Ylk(Т)+

D13*Fg(Т)+D14*(2*Yt[0]-Yp[0])

end

end;

For s:=1 to m-1 do

if s<>n then

begin

Fs:=Fn*(yt[s-1]+yt[s+1])+Cn*yt[s]+Bn*(yp[s-1]+ yp[s+1])-Dn*yp[s]+Tau2 *Fxt(S*Hx, T1);

Zs:=Dn-Bn*А[s-1]; А[s]:=Bn/Zs;

В[s]:=(Fs+Bn*В[s-1])/Zs

end

else

begin

Fs:=(Mg+Mh)/Tau2+Ts/Hs*(2-A[n-1]);

А[n]:=Ts/(Hx*Fs);

В[n]:=((Mg+Mh)/Tau2*(2*Yt[n]-(Yp[n])+Mh* Fxt*(n*Hx, Т)+Fg(Т)+Ts/Hx*b[n-1])/Fs

end;

case Ngr of

1: Y[m]:=Yr(Т);

2: if n<m then

Y[m]:=((D15-1)*(2*Yt[m]Yp[m])+

Hx/ Ts*Fr(Т)+В[m-1]/(D15-A[m-1]);

else

Y[m]:=((D18-1)*(2*Yt[m]Yp[m])+Hx/Ts*(Fr(Т)+

Fg(Т))+В[m-1]/(D18- А[m-1]);

3: if n<m then

Y[m]:=(D22*(2*Yt[m]-)(Yp[m])+D21*Yrk(Т)+

В[m-1])/(D23-A[m-1])

else

Y[m]:=(D21*Yrk(Т)+Hx/Ts*Fg(Т)+D26*(2*Yt[m]-Yp[m])+В[m-1])/(D27-A[m-1])

end;

For s:=m-1 downto 0 do

Y[s]:=А[s]*Y[s+1]+В[s];

Y[- 1]:=m;

Yp:=Yt;

Yt:=Y

End;