Турдалиев Ауезхан, к.т.н., доцент

Каз НТУ им. К.И.Сатпаева, г Алматы, Республика Казахстан

ОБ ИНТЕНСИВНОСТИ ОТКАЗОВ СЛОЖНЫХ СИСТЕМ.

Все производственные машины относятся к сложным механическим системам [1] , которые рассматриваются как единые целое. Объединение различных элементов узлов, механизмов в единую систему придает ей новые свойства, связанные с взаимодействием и взаимовлиянием ее составных частей. Поэтому, для решения проблемы надежности необходимо не только расчленение машины на отдельные элементы, а, главные, рассмотрение ее как сложной связанной системы, не идеализация состояния машины, а изучение свойственных ей ошибок функционирования, не использование статистика как основного источника информации о надежности, а прогнозирование возможного изменения технических характеристик машины с учетом процессов старения. Все эти положения является теми фундаментальными представлениями, на которых базируются основные разработки по оценке и обеспечению требуемого уровня надежности сложных машин./1/

Решение вышеизложенных поставленных задач нашло отражение в расмотрений характеристик надежности, как случайных величин, в различных плоскостях с пересечениями. Доставерность результатов, подтверждены с решениями примеров.

С другой стороны надежность как свойство изделия сохранять свое качество во времени, связана со многими общечеловеческими проблемами, такими, как эффективность, автоматизация, безопасность, экология, конкурентоспособность. Следовательно, рассматривая производственные машины и агрегаты необходимо оценить степень соответствие их параметров на вышеизложенные проблемы, т.е. уметь оценивать изменения состояние машины во времени на основании изучения трансформации ее выходных параметров./3/ Поэтому основным показателем надежности является вероятность безотказной работы, характеризующая состояние параметров качества находящих в допустимой области в течение заданного отрезка времени. Отказы в системе трактуются как выбросы допустимой области параметров.

1 Вычисление математического ожидания числа выбросов случайного процесса за заданный уровень.

Оценки вероятности безотказной работы содержат числовые характеристики числа выбросов векторного процесса v(t) из допустимой области Ω,в частности математическое ожидание, числа выбросов в течение отрезка времени [О,t]. Другой характеристикой выбросов является интенсивность числа выбросов в единицу времени (t), которые связано с математическим ожиданием числа выбросов на отрезке [О,t] соотношением

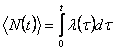, (1)

Рассмотрим вначале случай, когда v (t) – одномерный случайный процесс, а граница Γ допустимой области Ω есть прямая v= v_ж , причем допустимая область лежит ниже этой прямой ./2/

Пусть v(t) – непрерывный дифференцируемый случайный процесс с заданной совместной плотностью вероятности p( , ,t) процесса и его производной. Выбросу случайного процесса v(t) из допустимой области соответствует пересечение процессом v (t) уровня v_ж с положительной производной. Рассмотрим достаточно малый интервал времени ∆t. Обозначим через Q_к ( ∆t) вероятность того, что в пределах этого интервала процесс v(t) ровно k раз пересечет уровень v_ж с положительной производной/4/. Тогда математическое ожидание числа положительных пересечений за промежуток времени ∆t можно определить как

(2)

Математическое ожидание числа выбросов в единицу времени

Λ(t) связано с <N (∆t)> предельным соотношением

(3)

Так как интервал ∆t выбран достаточно малым, а процесс v (t) предлагается непрерывным и дифференцируемым, то вероятностями многократного пересечения Q₂(∆t),`Q₃ ,(∆t) и.т.д. можно пренебречь по сравнению с вероятностью Q₁(∆t) . Тогда формула (3) можно переписать в виде

(4)

Вероятность Q₁(∆t ) вычисляется через заданную совместную плотность вероятности p (, t) [I]:

Подстановка в формулу (4) после переход к пределу дает

(5)

В случае, когда уровень v_Ж(t) является детерминистической функцией времени, вероятность Q₁ (Δt) вычисляется аналогично, с той лишь разницей, что процесс v(t) может пересекать уровень v_ж (t) при выполнении условия v(t) > v_ж (t)/5/. Формула для математического ожидания числа выбросов в единицу времени в этом случае имеет вид

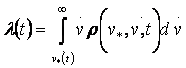(6)

Применение формул (5) и (6) для конкретных типов случайных процессов проиллюстрируем на примерах.

Пример I. Выбросы стационарного гауссовского процесса за фиксированный уровень. Совместная плотность вероятности этого процесса и его производной равна

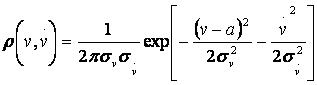
где α – математическое ожидание процесса v(t), σ²_U - его дисперсия, σ²_U - дисперсия производной. Существенно, что для стационарного процесса т.е. процесс и его производная стохастические независимы. Применение формулы (4.5) дает

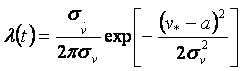
вводя обозначение для параметра, называемого эффективной частотой процесса, получим

(7)

Пример 2. Выбросы нестационарного гауссовского процесса за фиксированный уровень. В этом случае совместная плотность вероятности имеет вид

(8)

Здесь a(t) и – математическое ожидание и дисперсия процесса v (t), и – математическое ожидание и дисперсия производной, p (t) - в совпадающие моменты времени, который вводится как/6/

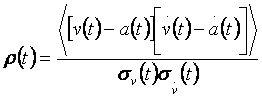
Для вычисления интеграла (5) введем новую переменную

в результате приходим к интегралу

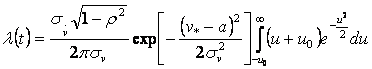
где

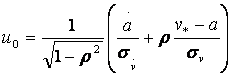
Если ввести функцию Лапласа в одной из следующих. двум форм:

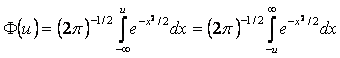(9)

то получим окончательную форму:

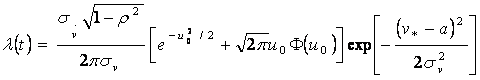(10)

Отметим, что числовые характеристики случайного процесса , входящие в эту формулу, является функциями времени. В случае стационарного процесса, для которого эти характеристики не зависят от времени, а ρ=à=0, формула (10) переходит в формулу (7).

Пример 3. Выбросы нестационарного гауссовкого процесса за переменный уровень. Для уровня v_ж(t), неслучайным образом изменяющегося во времени, математическое ожидание числа выбросов в единицу времени находится по формуле (6). Интеграл вычисляется аналогично тому, как это было сделано в предыдущем примере. Окончательное выражение для l(t) имеет вид (10), если вместо (8)

Ввести обозначение

(11)

Пример 4. Выбросы стационарного ралеевского процесса за фиксированный уровень. Для стационарного процесса, распределенного по закону Рэлея, совместная плотность вероятности процесса и его производной равна [7]:

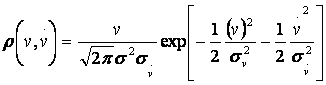
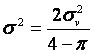(12)

Вычисление интеграла (5) не представляет трудности. Окончательно получим выражение

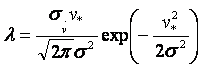(13)

При вычислении интегралов типа (5) или (6) нужно знать совместную плотность вероятности случайного процесса и его производной/7/. Для определения этой плотности вероятности должна быть найдена двухточечная совместная плотность вероятности процесса p_J (v_1, v₂ ), где v₁=v(t₁), v₂=v(t₂). Совместная плотность вероятности процесса и его производной определяется после замены переменных v =v_1,v =(v₂ – v₁)/ ∆ t и перехода к пределу при ∆t = t₁ – t₂ →0:

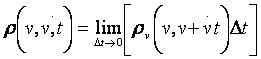(14)

Отсюда вытекает другой способ вычисления характеристик выбросов случайного процесса за случайный уровень : достаточно рассмотреть выбросы вспомогательного процесса u(t)=v(t)-w(t) за неслучайный нулевой уровень [5]. Так как распределение разности двух гауссовских процессов будет также гауссовским, то применение формулы при v_*=0, естественно, если вместо параметров s_v , s_v , <v>,<v’> и r использовать соответствующие параметры для вспомогательного процесса u(t). Этот результат является следствием устойчивости нормального распределения по отношению линейного преобразования.

Литература:

1.Андреев А.А. Расчет деталей машин при сложном напряженном состоянии. М. Машиностроение, 1981г.

2.Гойзман Э.И. Моделирование производственных процессов на шахтах. М., Недра, 1977г.

3.Спиваковский А.О., Дьячков В.К. Транспортирующие машин. М., Машиностроение, 1983г.

4.Макаров Б.П. Нелинейные задачи статистической динамики машин и приборов. М., Машиностроение, 1983, 264с.

5.Ларин В.В. Статистическое задачи виброзащиты. Киев, Наукова думка, 1974-127с.

6.Коловский М.З. Нелинейная теория виброзащитных систем. М., Наука 1966-318с.

7.Липцер Р.Ш., Ширяев А.Н., Статистика случайных процессов. М. Наука 1974-696с