Экономические науки /8. Математические методы в экономике

К.т.н., проф. Иманалиев З.К., к.ф-м.н, доц. Аширбаев Б.Ы.

Кыргызский государственный технический университет им.И.Раззакова, Кыргызская Республика.

РЕШЕНИЕ ЗАДАЧИ УПРАВЛЕНИЯ ЭКОНОМИКОЙ НА МАКРОУРОВНЕ НА ОСНОВЕ ДИСКРЕТНОЙ МОДЕЛИ ОПТИМИЗАЦИИ С МАЛЫМ ШАГОМ

В данной работе рассмотрена задача управления экономикой на макроуровне. На основе дискретной модели оптимизации с малым шагом предложен алгоритм решения задачи и исследован оптимальные решения применительно к конкретным экономическим системам.

Рассмотрим экономический процесс, который характеризуется в каждый момент времени t набором переменных X, Y, C, K, L, J где X - интенсивность валового продукта, Y - интенсивность конечного продукта, C - непроизводственное потребление, J - валовые капитальные вложения, K - объем основных производственных капиталов, L - трудовые ресурсы.

Взаимозависимости этих переменных определяются следующими соотношениями [1]:

(1)

или (2)

где прирост основных капиталов в течение короткое время, коэффициент амортизации, a – коэффициент прямых затрат малое время или малый шаг дискретности, доля непроизводственного потребления, Здесь дискретные моменты времени определяются как:

(3)

Размеры валового продукта определяются заданной производственной функцией т.е. Будем предполагать, что производственная функция непрерывна и дважды дифференцируема причем для нее имеют место следующие соотношения:

Также предполагается, что отдача от масштаба производства постоянна, т.е. для любого числа имеет место равенство При исследовании данного процесса учитываются следующие ограничения: где уровень капитала в начальный момент времени, заданный уровень капитала. Допустимый процесс представляется совокупностью функции которые удовлетворяют условиям (1) – (5).

Задача управления данной экономикой состоит в следующем: найти такой процесс который обеспечивал бы наибольшее среднедушевое потребление на отрезке времени [0, T] с учетом дисконтирования потребления

(4)

где взвешивающая функция, коэффициент дисконтирования.

Проведем редукцию задачи. Для этого введем относительные переменные [3]: величина капитала на одного рабочего (капиталовооруженность), среднедушевое потребление, производительность труда. Полагаем, что прирост трудовых ресурсов происходит с постоянным темпом, равным n. Тогда где или

(5)

Преобразование функционала (4) к относительным переменным имеет вид

или (6)

Тогда редуцированную задачу можно сформулировать так: найти такой процесс который доставляет минимум соотношения (6) при ограничениях:

(7)

где

Подобная задача (для непрерывной момент времени t) рассмотрена в [2]. Предположим, что размеры конечного продукта определяются производственной функцией Кобба-Дугласа (используется дискретный аналог этой функции). Тогда производительность труда x определяется как [3]

(8)

где коэффициент определяющий темп роста технического процесса, коэффициент эластичности выпуска по производственным капитальным средствам, коэффициент выпуска по труду.

Уравнение (7) и функционал (6) с учетом (8) записываются в виде:

(9)

(10)

Рассмотрим задачу (6), (9). Введем новую функцию

(11)

Тогда (12)

где

следует заметить, что при имеем

Пусть , тогда из (9) будем иметь

(13)

или

Правая часть (14) дает нам функцию, стоящую под суммы в функционале (6).

Введем обозначение Эта функция не зависит от управление u. Необходимым условием минимума по k является равенство нулю частной производной: или

(15)

Отсюда будем иметь (16)

Полученное назовем магистралью данной дискретной модели экономики. С учетом (15) из (13) находим управление u:

или так как то Теперь, полагая из (9), (12) получим

(17)

Введем

Потребуем, чтобы эта функция не зависела от k . Тогда

(18)

Отсюда будем иметь формулу для оптимальной капиталовооруженности

(19)

С учетом (18) из (17) получим

(20)

C другой стороны с учетом (19) из (11) будем иметь

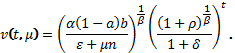(21)

Формулу (21) можно использовать для определения оптимальной капиталовооруженности при различных значениях коэффициента дисконтирования При

(22)

Если считать время t непрерывной, то функция (21) является решением следующего дифференциального уравнения

(23)

с начальным условием (22). Если учесть, что то из (23) получается разностное уравнение

(24)

Сравнивая уравнения (20) и (24) получим

(25)

Условие (25) имеет место, если

(26)

При для функции и имеют следующие предельные значения

В заключении необходимо отметить, что предложенный способ позволяет:

- получить упрошенный алгоритм решения задачи, который сокращает объем вычислительных работ;

- определить скорость изменения наличного капитала на одного рабочего и получить оценку влияния малого параметра на изменения выхода на магистраль.

ЛИТЕРАТУРА

1. Интрилигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1975.

2. Иманалиев З.К., Баракова Ж.Т. Оценка оптимального развития экономики на основе оптимизационной модели //Известия Томск. политехн. ун-та, 2007. Т. 310, №2. С. 200-204.

3. Основы теории оптимального управления / В.Ф. Кротов, Б.А. Лагоша, С.М. Лобанов, Н.И. Данилина, С.И. Сергеев. М.: Высшая школа, 1990.