Современные информационные технологии/ Информационная безопасность

Аненко М.Н., Пархоменко И.И.

Национальный авиационный университет

УСЛОВИЯ ДОСТИЖЕНИЯ ЗАДАННОГО УРОВНЯ

ЗАЩИЩЕННОСТИ СТЕГОСИСТЕМ К ОБНАРУЖЕНИЮ ФАКТА ПЕРЕДАЧИ СООБЩЕНИЯ

На сегодняшний день все острее встаёт вопрос касательно защиты информации по средствам стеганографических методов. Это обусловлено стремительными темпами развития информационной техники, которая способна взламывать даже шифры повышенной стойкости, созданием которых занимается криптография. Стеганографические методы защиты информации построены по иному принципу, что позволяет эффективно защитить информационные ресурсы. К тому же, есть существенное преимущество перед криптографическими методами. Эти преимущества выражены в том, что для того, что бы прочесть скрытое сообщение, надо его перехватить. На противодействие перехватам как раз, и направлена большая часть усилий стеганографии.

Можно выделить два больших направления в которых используются стеганографические разработки, первое – цифровые водяные знаки (ЦВЗ), которые призваны защитить авторское право, и второе – средства по сокрытию факта передачи информации, которые в свою очередь разделяются по конкретным направлениям, на которые делается уклон при создании той или иной системы. В качестве направлений имеется в виду повышенный уровень защищенности к определенному роду негативных воздействий.

И так, в дельнейшем речь пойдет о конкретном виде устойчивости стегосистемы, а именно, устойчивости к обнаружениям факта передачи стего, будут определены критерии и условия достижения заданного уровня защищенности с помощью математических моделей.

Для анализа стойкости стеганографических систем к обнаружению факта передачи скрываемых сообщений необходимо создать модель стегосистемы с нарушителем:

· Нарушитель «Н» способен наблюдать за каналом передачи сообщений.

· Обмен информацией осуществляется между абонентами «А» и «Б».

· Нарушитель «H» не знает о том какие сообщения пересылаются по сети «S» - содержащие стего, или «С» - произвольный контейнер.

· «А» может находиться в двух состояниях: активном (осуществляется передача скрытого сообщения «S»), и пассивном ( «А» передаёт пустой контейнер «С»).

Допустим абонент «А» сам может генерировать адаптивной контейнер «С» для помещения в него исходного сообщения «М». Получив стего, «Б» должен быть в состоянии извлечь из него сообщение «М» используя ключ «К». К тому же, наша стегосистема должна отвечать требованиям теории информации:

· Формируемое отправителем стего однозначно определяется значением контейнера «C», ключом «K», и сообщением «M».

· Для получателя и нарушителя вероятность того, что они знают какое сообщение будет отправлено не должно быть больше 0, в противном случае по каналу передачи не передаётся неизвестной информации, тем самым теряется сам смысл сокрытия информации. Надо также добавить, что для цифровых водяных знаков – ЦВЗ данное условие может не выполняться.

· Получатель должен однозначно восстановить скрываемое сообщение переданное ему.

Предположим, что всем из участников данной модели известны вероятностные распределения множеств скрываемых сообщений, стего, контейнеров, и ключей. К тому же, получателю «Б» известно когда отправитель «А» находится в активном состоянии. Нарушитель «С» наблюдает передаваемы сообщения и должен определить, передаётся скрываемая информация или нет. «С» производит анализ всех перехваченных сообщений и пытается определить к какому распределению относится данная информация (к распределению стего или контейнеров). Если нарушитель «С» способен определить к какому распределению относится передаваемая в канале связи информация, то факт скрытой передачи информации от «А» к «Б» доказан, и данная система обмена является не стойкая.

В данной модели, нарушителю известно вероятностное распределение как пустых контейнеров P_c так и контейнеров со стего Р_s. Все множество наблюдаемых контейнеров и стеганограмм обозначим Q. Нарушитель в процессе наблюдения сообщений которые будут передаваться по сети может выдвинуть две гипотезы H_c и H_s. Если справедлива гипотеза H_c, то сообщение q соответствует распределению P_c, а если справедливо H_s, то распределению Р_s. Правило принятия решения заключается в разбиении множества Q на два подмножества, что бы каждому сообщению назначить одну из гипотез. В данном случае различают два рода ошибок: ошибка первого рода (ложная тревога), и ошибка второго рода (пропуск цели). Соответственно вероятность ошибки первого рода – α, вероятность ошибки второго рода – β.

Оптимальное решение будем принимать согласно критерию Неймана-Пирсона. Правило принятия решения зависит от порога V. Вероятность наступления события α может быть минимизировано с помощью назначения такой гипотезы H_c, только тогда, когда выполняется следующее соотношение:

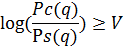
Основным критерием для различения гипотез является относительная энтропия:

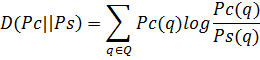
Относительная энтропия почти всегда равна 0 или не отрицательна между двумя распределениями, если только они совпадают.

Покажем как можно использовать относительную энтропию между распределениями _и для оценки стойкости стегосистемы при воздействии на неё пассивного противника.

Итак, стегосистема называется стойкой от пассивного нарушителя если:

Где – параметра получаемый при расчете относительной энтропии.

Если параметр , то такая система является совершенной. Это означает, что вероятность обнаружения факта передачи сообщения не изменяется от того, наблюдает ли нарушитель информационный обмен от отправителя А к отправителю Б или нет.

Рассмотрим условия обеспечения стойкости. Будем исходить из соотношений между относительной энтропией и размером алфавита X для произвольных переменных S и С.

Если переменная S равновероятно и независимо распределена, то:

Если переменная С является равновероятной и независимой то выполняется условие: , и тогда . Соответственно, если использовать вместо контейнера случайные последовательности то скрываемые сообщения тоже будут описаны случайными последовательностями. Таким образом сформированное стего S не будет иметь никаких статистических отличий от пустых контейнеров. К сожалению реальные передаваемые по каналу связи сообщения используемые в стегосистеме как пустые контейнеры, далеки от данной модели. Поэтому такая передача сразу же демаскирует скрытый канал передачи. Для решения данной проблемы предлагается удалять часть изображения и в сжатые таким образом контейнеры встраивать сообщения, таким образом характеристики стего приближаются к характеристикам случайного источника.

Если стегосистема является - стойкой против нарушителя, то вероятность β необнаружения факта скрытой связи и вероятность α ошибочного факта установления факта скрытой связи удовлетворяет неравенству

Где: верхняя граница .

В частном случае, если , то .

Из этого следует, что вероятность пассивного состояния А должна быть вомного раз больше вероятности её активного состояния, и что использование контейнеров с учетом их модификации должно во много раз больше скрываемых сообщений.

Литература:

1. «Цифровая обработка изображений» Б.Яне, Техносфера, Москва 2007. 584с.

2. «Цифровая стеганография» Грибунин В.Г., Оков И.Н., Туринцев И.В. СОЛОН-ПРЕСС, 2009 г. 264 стр.

3. «Основы современной криптографии для студентов в информационных технологиях» Рябко Б.Я., Фионов А.Н. Научный мир, 2004г. 173 стр.

4. «Современные шифры» Зубов А.Ю. Москва «Гелиос АРВ» 2003г. 160 стр.

5. «Современная криптология» Ж. Брассор. Полимед, Москва 2009. 176с.

6. «Цифровая обработка изображений» Б.Яне, Техносфера, Москва 2007. 584с.