К. т. н., профессор каф. САПР Эттель В. А.,

студентка группы СИБ-09-2 Адащенко Д. С.

Карагандинский государственный технический университет

Возможности квантовой криптографии

Существуют различные методы шифрования, используемые в криптографии, но в данной статье речь пойдёт о качественно новом методе – квантовой криптографии.

В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография сосредоточена на физике, рассматривая случаи, когда информация переносится с помощью объектов квантовой механики.

В сравнении с алгоритмом шифрования, например RSA, в основе шифра которого лежит идея того, что на простых компьютерах невозможно решить задачу разложения очень большого числа на простые множители, так как данная операция потребует астрономического времени и экспоненциально большого числа действий, квантовый алгоритм позволяет найти за конечное и приемлемое время все простые множители больших чисел, и, как следствие, взломать шифр RSA. Таким образом, квантовый криптоанализ может быть применён ко всем классическим шифросистемам. Необходимо только создание квантового компьютера, способного развить достаточную мощность.

Квантовая криптография — очень перспективная часть криптографии, так как технологии, используемые там, позволяют вывести безопасность информации на высочайший уровень.

Технология квантовой криптографии опирается на принципиальную неопределённость поведения квантовой системы — невозможно одновременно получить координаты и импульс частицы, невозможно измерить один параметр фотона, не исказив другой. Это фундаментальное свойство природы в физике известно как принцип неопределённости Гейзенберга, сформулированный в 1927 г., является одним из краеугольных камней квантовой механики.

Принцип неопределённости – фундаментальное положение квантовой теории, утверждающее, что любая физическая система не может находиться в состояниях, в которых координаты её центра инерции и импульс одновременно принимают вполне определённые, точные значения. Количественно принцип неопределённости формулируется следующим образом. Если ∆x – неопределённость значения координаты x центра инерции системы, а ∆p_x – неопределённость проекции импульса p на ось x, то произведение этих неопределённостей должно быть по порядку величины не меньше постоянной Планка ħ. Аналогичные неравенства должны выполняться для любой пары т. н. канонически сопряженных переменных, например для координаты y и проекции импульса p_y на ось y, координаты z и проекции импульса p_z. Если под неопределённостями координаты и импульса понимать среднеквадратичные отклонения этих физических величин от их средних значений, то принцип неопределённости для них имеет вид:

∆p_x ∆x ≥ ħ/2, ∆p_y ∆y ≥ ħ/2, ∆p_z ∆z ≥ ħ/2

Используя квантовые явления, можно спроектировать и создать такую систему связи, которая всегда может обнаруживать подслушивание. Это обеспечивается тем, что попытка измерения взаимосвязанных параметров в квантовой системе вносит в неё нарушения, разрушая исходные сигналы, а значит, по уровню шума в канале легитимные пользователи могут распознать степень активности перехватчика.

Существует несколько квантовых протоколов. В данной статье будет описан протокол BB84.

В протоколе BB84 используются 4 квантовых состояния фотонов, например, направление вектора поляризации, одно из которых Алиса выбирает в зависимости от передаваемого бита: 90° или 135° для «1», 45° или 0° для «0». Одна пара квантовых состояний соответствует 0(|0(+)>) и 1(|1(x)>) и принадлежит базису «+». Другая пара квантовых состояний соответствует 0(|0(x)>) и 1(|1(x)>) и принадлежит базису «х». Внутри обоих базисов состояния ортогональны, но состояния из разных базисов являются попарно неортогональными (неортогональность необходима для детектирования попыток съема информации).

Квантовые состояния системы можно описать следующим образом:

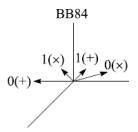
Рисунок 1 – Состояния поляризации фотонов, используемые в протоколе ВВ84

Этапы формирования ключей:

1) Алиса случайным образом выбирает один из базисов. Затем внутри базиса случайно выбирает одно из состояний, соответствующее 0 или 1 и посылает фотоны (рисунок 2):

Рисунок 2 - Фотоны с различной поляризацией

2) Боб случайно и независимо от Алисы выбирает для каждого поступающего фотона: прямолинейный (+) или диагональный ( х ) базис (рисунок 3):

Рисунок 3 - Выбранный тип измерений

Затем Боб сохраняет результаты измерений:

Рисунок 4 - Результаты измерений

3) Боб по открытому общедоступному каналу связи сообщает, какой тип измерений был использован для каждого фотона, то есть какой был выбран базис, но результаты измерений остаются в секрете;

4) Алиса сообщает Бобу по открытому общедоступному каналу связи, какие измерения были выбраны в соответствии с исходным базисом Алисы (рисунок 5):

Рисунок 5 - Случаи правильных замеров

5) далее пользователи оставляют только те случаи, в которых выбранные базисы совпали. Эти случаи переводят в биты (0 и 1), и получают, таким образом, ключ (рисунок 6):

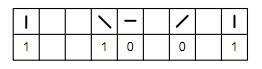
Рисунок 6 - Получение ключевой последовательности по результатам правильных замеров

Число случаев, в которых выбранные базисы совпали, будет составлять в среднем половину длины исходной последовательности, т.е. n = ½ (пример определения количества фотонов, принятых Бобом, показан в таблице 1).

Таблица 1- Формирование квантового ключа по протоколу ВВ84

Двоичный сигнал Алисы	0	1	0	1
Поляризационный код Алисы
Детектирование Бобом
Двоичный сигнал Боба	0	1	?	?

Таким образом, в результате передачи ключа Бобом в случае отсутствия помех и искажений будут правильно зарегистрированы в среднем 50% фотонов.

Однако идеальных каналов связи не существует и для формирования секретного ключа необходимо провести дополнительные процедуры поиска ошибок и усиления секретности. При этом для части последовательности бит пользователей, в которых базисы совпали, через открытый общедоступный канал связи случайным образом раскрываются и сравниваются значения бит. Далее раскрытые биты отбрасываются. В идеальном квантовом канале (без шума) достаточно выявить несоответствие в одной раскрытой позиции для обнаружения злоумышленника. В реальной ситуации невозможно различить ошибки, произошедшие из-за шума и из-за воздействия злоумышленника. Известно, что если процент ошибок QBER ≤ 11%, то пользователи из нераскрытой последовательности, после коррекции ошибок через открытый общедоступный канал связи и усиления секретности, могут извлечь секретный ключ, который будет у них одинаковым и не будет известен Еве. Ключ, полученный до дополнительных операций с последовательностью, называется "сырым" ключом.

При коррекции ошибок эффективным способом для согласования последовательностей Алисы и Боба является их «перемешивание» для более равномерного распределения ошибок и разбиение на блоки размером k, при котором вероятность появления блоков с более чем одной ошибкой пренебрежимо мала. Для каждого такого блока стороны производят проверку четности. Блоки с совпадающей чётностью признаются правильными, а оставшиеся делятся на несколько более мелких блоков, и проверка четности производится над каждым таким блоком, до тех пор, пока ошибка не будет найдена и исправлена. Процедура может быть повторена с блоками более подходящего размера. Наиболее мелкие блоки отбрасываются при наличии в них ошибки.

Когда в каком-либо блоке количество ошибок окажется чётным, то даже с оптимальным размером блока некоторые из них могут быть не выявлены. Для их исключения производят перемешивание последовательности бит, разбиение её на блоки и сравнение их чётности производится ещё несколько раз, каждый раз с уменьшением размера блоков, до тех пор, пока Алиса и Боб не придут к выводу, что вероятность ошибки в полученной последовательности пренебрежимо мала.

В результате всех этих действий Алиса и Боб получают идентичные последовательности бит. Эти биты и являются ключом, с помощью которого пользователи получают возможность кодировать и декодировать секретную информацию и обмениваться ей по незащищённому от съема информации каналу связи.

В заключение хочу сказать, что последние разработки в области квантовой криптографии позволяют создавать системы, обеспечивающие практически 100%-ю защиту ключа и ключевой информации. Используются все лучшие достижения по защите информации как из классической криптографии, так и из новейшей "квантовой" области, что позволяет получать результаты, превосходящие все известные криптографические системы. Можно с уверенностью говорить, что в ближайшем будущем вся криптографическая защита информации и распределение ключей будут базироваться на квантово-криптографических системах.

Литература:

1. C. Gobby, Z. Yuan, and A. Shields, "Quantum key distribution over 122 km of standard telecom fiber", Appl. Phys. Lett. 84, 3762-3764 (2004).

2. C. Bennett and G. Brassard, "Quantum cryptography: Public key distribution and coin tossing", in Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (Institute of Electrical and Electronics Engineers, New York,1999)

3. A. Muller, H. Zbinden, and N. Gisin, "Quantum cryptography over 23 km in installed under-lake telecom fiber", Europhysics Lett (1996).

4. Д.М. Голубчиков. “Применение квантовых усилителей для съема информации с квантовых каналов распределения ключа”, Известия ТТИ ЮФУ(2008).

5. К.Е. Румянцев, И.Е. Хайров, В.В. Новиков, “Анализ возможности несанкционированного доступа в квантово-криптографическом канале”, Материалы международной научной конференции «Анализ и синтез как методы научного познания» (2004).