Галеева З.Р.

Лесосибирский педагогический институт – филиал ФГОАУ ВПО «Сибирский федеральный университет»

Применение движений к решению экстремальных задач на построение

В математике существует целый класс задач, в которых при заданных условиях нужно отыскать наибольшее или наименьшее значение некоторой величины. Оба понятия — максимум и минимум — объединяются термином "экстремум". Одним из видов экстремальных задач являются задачи на построение, наиболее распространенным методом решения которых является метод геометрических преобразований. Рассмотрим применение различных видов движения к решению задач на максимум и минимум.

Задача 1. В данном остроугольном треугольнике ABC найти точку P, для которой сумма расстояний до вершин треугольника минимальна (задача Ферма).

Решение. Рассмотрим поворот около вершины А на 60̊. Пусть при этом повороте (рис.1). Так как треугольник APP’ равносторонний, то AP = PP’ и поэтому

AP + PB + PC = PP’ + P’B’ + PC = B’P’ + P’P + PC.

Эта сумма минимальна тогда и только тогда, когда точки B’, P’, P, С лежат на одной прямой.

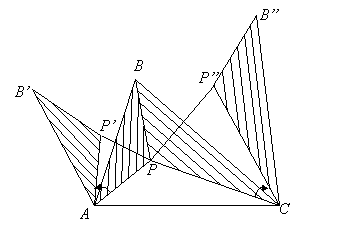
рис. 1

Аналогично рассмотрим поворот около вершины С на 60̊, при котором тогда

AP + PB + PC = AP + P”B” + PP” = AP + PP” + P”B” = min,

если АB” – прямая. Таким образом, искомая точка P является точкой пересечения прямых B’С и АB”.

Задача 2. Дан угол XAY и точка O внутри его. Проведите через точку O прямую, отсекающую от данного угла треугольник наименьшей площади.

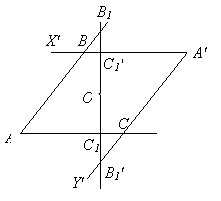
рис. 2

Решение. Рассмотрим угол X¢A¢Y¢, симметричный углу XAY относительно точки O. Пусть B и C – точки пересечения сторон этих углов. Обозначим точки пересечения прямой, проходящей через точку O, со сторонами углов XAY и X¢A¢Y¢ через B₁, C₁ и B₁¢, C₁¢ соответственно (рис. 2). Так как то. Площадь треугольника AB₁C₁ минимальна, если B₁ B и C₁ C, т. е. искомой прямой является BC.

Задача 3. Дан угол и внутри него точка М. Найти на сторонах угла такие точки Х и Y, чтобы периметр треугольника MXY был наименьшим.

Решение. Предположим, что задача решена и отрезок искомый. Для спрямления ломанной MXYM расположим отрезки, равные данным, на одной прямой, для чего используем симметрию относительно прямых OA и OB.

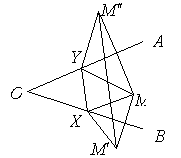
рис. 3

Тогда

если лежат на одной прямой.

Задача 4. По разные стороны от реки находятся пункты A и D. Где нужно построить мост, чтобы путь из A в D через него был кратчайшим?

Решение. Пусть параллельные прямые b и c изображают берега реки (рис. 4, а). Построим отрезок AA’, перпендикулярный b и равный расстоянию межде берегами h (рис. 4, б).

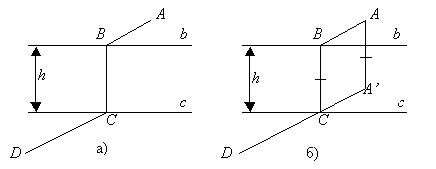
рис. 4

Если BC – искомый мост, то четырехугольник AA’CB – параллелограмм и, следовательно, AB + BC + CD = AA’ + A’C + CD. Путь от A до D равен AA’ + A’C + CD и имеет наименьшую длину, если A’C + CD принимает наименьшее значение. Это произойдет в случае, если A’, C и D лежат на одной прямой. Таким образом, для построения BC нужно: построить отрезок AA’, перпендикулярный b и равный h; провести прямую A’D и найти ее точку пересечения C с прямой с; провести BC, перпендикулярно с.

5. Применение скользящей симметрии. На данной прямой a отложить отрезок XY данной длины k так, чтобы длина ломаной MXYN была наименьшей, если точки M и N лежат по одну сторону от прямой a.

Решение. Предположим, что задача решена и отрезок XY – искомый. Поскольку его длина постоянна, то длина ломаной MXYN будет наименьшей, когда будет минимальной сумма отрезков MX и YN. Сблизим эти отрезки с помощью параллельного переноса на вектор YX: N→N’, NY→N’X / NY = N’X.

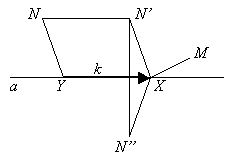
рис. 5

Задача сводится к нахождению точки X на прямой такой, что MX + XN’ = min. Отрезки MX и XN’ на одной прямой расположить нельзя, но можно расположить равные им отрезки MX и XN”, где N” – точка, симметричная точке N относительно прямой a. Искомая точка X является точкой пересечения прямой a и отрезка MN”, где N” – образ точки N при скользящей симметрии, осью которой служит прямая a, а длина вектора переноса равна k.

Таким образом, проанализировав применение движений к решению экстремальных задач можно сделать вывод о том, что способ применения преобразований различен: параллельный перенос дает нам возможность сблизить различные отрезки и тем самым исключить отрезок постоянной длины; осевая симметрия используется для «спрямления» ломаной, в задачах на нахождение наименьшей длины ломаной; поворот (в частности, центральная симметрия) позволяет нам расположить точки и их образы на одной прямой для выявления экстремальных свойств; а скользящая симметрия используется в задачах, в которых необходимо сначало сблизить данные отрезки, а затем расположить их на одной прямой.