Математика. Прикладная математика.
Д.ф.-м.н.,
проф. Фетисов В.Г., Панина И.И.
Южный
математический институт ВНЦ РАН,
г.
Владикавказ, Россия
ОПЕРАТОР ХАРДИ В ПРОСТРАНСТВЕ МАРЦИНКЕВИЧА –
ВНЕШНЕЙ СРЕДЕ ДИНАМИЧЕСКИХ интегральных
СИСТЕМ
Как известно [1], такие элементы, как:
объект управления, исполнительный элемент, усилитель, измерительное устройство
(датчик), являются функционально необходимыми, без которых рассматриваемая
система существовать не может.
Системы, в принципиальную схему которых
входят только вышеуказанные элементы, в общем случае не обеспечивают
нормального хода ее рабочего процесса, так как при соблюдении лишь необходимых
условий ее функционирования, нельзя устранить отклонение режима от заданного,
обусловленное, кроме того, различными экзогенными факторами.
Заметим, что наряду с вышеуказанными
элементами теории систем не меньшую роль для описания качества их работы служит
и внешняя среда, в которой функционирует объект управления, (рассматриваемая в
терминах топологий некоторых сигналов и передаточных функций).
Например, качеством динамического процесса
в системе слежения может являться размер нормы сигнала ошибки, рассматриваемой в
том или ином функциональном пространстве.
Разнообразие и широта задач современной
теории управления диктует необходимость изучения и детальной структуры внешней
среды системы, элементами которой являются как различные линейные
топологические пространства (локально ограниченные, векторные решетки,
нормированные алгебры), так и действующие в них различные абстрактные объекты
(функционалы, операторы, функторы).
Если банаховы пространства, являющиеся
полными нормированными, и поведение в них традиционных типов операторов «вход-выход»,
служащих основой синтеза динамической системы, исследованы подробно, то класс
локально невыпуклых топологических пространств и действующих в них линейных и,
особенно, нелинейных операторов к настоящему времени не подвергся сколь-нибудь
полному изучению. Особый интерес представляют открытые вопросы локально
ограниченных функциональных пространств и операторов, действующих в них (см., например,
[2]).
Локально ограниченное пространство
Е измеримых функций, заданных на компакте
![]() , имеющем
, имеющем ![]() -конечную меру, называется симметричным, если выполняются
два условия:
-конечную меру, называется симметричным, если выполняются
два условия:
а) если ![]() и
и ![]() , где у(t) – измеримая на
, где у(t) – измеримая на ![]() функция, то
функция, то ![]() и
и ![]() ;
;
б) если ![]() и обе функции
и обе функции ![]() ,
, ![]() равноизмеримы, то
равноизмеримы, то
![]() и
и ![]() .
.
В частности, в необходимых для
приложений случаях можно считать ![]() [0,1]. Поскольку пространство Е содержит константы, то в силу условия а) все характеристические
функции
[0,1]. Поскольку пространство Е содержит константы, то в силу условия а) все характеристические
функции ![]() измеримых
множеств
измеримых
множеств ![]() принадлежат
исходному пространству Е. Функцию
принадлежат
исходному пространству Е. Функцию ![]() , где
, где ![]() , принято считать фундаментальной функцией исходного
локально ограниченного симметричного пространства Е.
, принято считать фундаментальной функцией исходного
локально ограниченного симметричного пространства Е.
Пусть ![]() – фундаментальная
функция некоторого симметричного пространства Е. Тогда она обладает следующими свойствами:
– фундаментальная
функция некоторого симметричного пространства Е. Тогда она обладает следующими свойствами: ![]() не убывает на
[0,1]; функция
не убывает на
[0,1]; функция ![]() не возрастает на
(0,1];
не возрастает на
(0,1]; ![]() и
и ![]() при
при ![]() . Будем в дальнейшем предполагать, что фундаментальная
функция
. Будем в дальнейшем предполагать, что фундаментальная
функция ![]() произвольного
симметричного пространства Е вогнута.
произвольного
симметричного пространства Е вогнута.
Если ![]() – фундаментальная
функция некоторого симметричного пространства Е1, то и функция
– фундаментальная
функция некоторого симметричного пространства Е1, то и функция
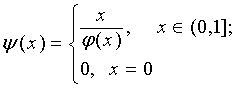
является фундаментальной для некоторого
симметричного пространства Е2.
Примерами
локально ограниченных функциональных пространств сигналов, описывающих
качественное поведение многих динамических систем, могут служить пространства
Лоренца, Марцинкевича, Лебега, Орлича и Харди как вещественно-, так и
комплекснозначных функций. (см. подробнее монографию [3]).
Пространство Лоренца ![]() представляет
собой линейное множество измеримых на отрезке [0,1] функций
представляет
собой линейное множество измеримых на отрезке [0,1] функций ![]() , для которых конечна квазинорма, имеющая вид:
, для которых конечна квазинорма, имеющая вид:
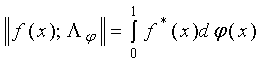 , (1)
, (1)
где через ![]() обозначена невозрастающая
функция, равноизмеримая с
обозначена невозрастающая
функция, равноизмеримая с ![]() на [0,1].
на [0,1].
Пространство Марцинкевича ![]() , есть множество измеримых на отрезке [0,1] функций
, есть множество измеримых на отрезке [0,1] функций ![]() , для которых конечна квазинорма, имеющая вид:
, для которых конечна квазинорма, имеющая вид:
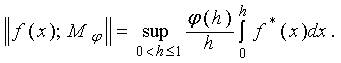 (2)
(2)
Пространства ![]() и
и ![]() с квазинормами
(1) и (2) являются локально ограниченными симметричными пространствами соответственно
с одной и той же фундаментальной функцией
с квазинормами
(1) и (2) являются локально ограниченными симметричными пространствами соответственно
с одной и той же фундаментальной функцией ![]() .
.
Другими представителями локально
ограниченных симметричных пространств являются пространства Лебега ![]() и Орлича
и Орлича ![]() . В качестве модельного нами выбрано локально
ограниченное пространство Марцинкевича измеримых на заданном компакте
. В качестве модельного нами выбрано локально
ограниченное пространство Марцинкевича измеримых на заданном компакте ![]() функций как
наиболее широкое для применения в теории интерполяции операторов.
функций как
наиболее широкое для применения в теории интерполяции операторов.
Во многих приложениях к синтезу
динамических систем приходится рассматривать следующий интегро-функциональный оператор:
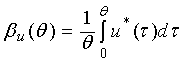 ,
, ![]() (3)
(3)
(здесь ![]() – измеримое множество,
лежащее в конечномерном пространстве), представляющий собой так называемый
оператор Харди.
– измеримое множество,
лежащее в конечномерном пространстве), представляющий собой так называемый
оператор Харди.
Он, как известно, ограничен в
банаховом пространстве Лебега ![]() , норма в котором ||u; Lα||=
, норма в котором ||u; Lα||=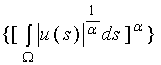 , 0<
, 0<![]() <1, причем
<1, причем
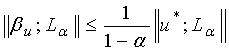 . (4)
. (4)
Этот фундаментальный результат
Харди нами обобщается на случай локально ограниченных пространств Марцинкевича,
для которых
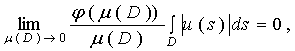 (5)
(5)
(где D – измеримое подмножество ![]() ).
).
Здесь φ(λ) такая функция, что, как φ(λ), так и φ*(λ)= 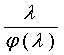 – неубывающие
вогнутые на положительной полуоси
(0, ∞)) функции, причем
– неубывающие
вогнутые на положительной полуоси
(0, ∞)) функции, причем
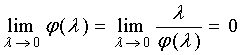 . (6)
. (6)
Квазинорма
в локально ограниченном пространстве Марцинкевича ![]() с учетом
равноизмеримости имеет следующий вид:
с учетом
равноизмеримости имеет следующий вид:
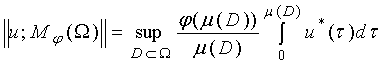 , (7)
, (7)
где u*(τ) –
определенная на отрезке [0, μ(Ω)], неотрицательная, невозрастающая
функция, равноизмеримая с |u(s)|.
Без ограничения общности можно
считать, что функция u*(τ) на [μ(Ω),∞) равна нулю.
Пусть
функция φ(λ) такова, что интеграл
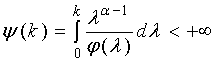 (8)
(8)
(т.е. сходится), и кроме того, имеет место
неравенство
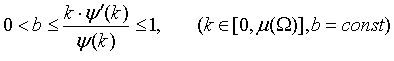 . (9)
. (9)
В
этом случае функция φ(λ) является квазистепенной. В частности, таковой будет степенная функция φ(λ)=![]() .
.
Из условия (8) непосредственно следует
оценка ![]() , а это, как известно,
обеспечивает вложение пространств
, а это, как известно,
обеспечивает вложение пространств ![]() . Для соответствующих квазинорм имеет место неравенство
. Для соответствующих квазинорм имеет место неравенство
![]() , (10)
, (10)
где постоянная вложения
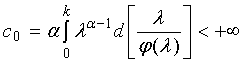 . (11)
. (11)
Используя
оценки (8) и (9), получим
![]() (12)
(12)
ТЕОРЕМА
1. Пусть выполнены условия (8) и (9). Тогда оператор Харди определен и
ограничен в пространстве ![]() , причем
, причем
![]() (13)
(13)
где c1>0 – постоянная, не зависящая от выбора
функции u*(θ).
◄
Пусть ![]() . Тогда, используя соотношения (9), (10) и (12), получим
оценку, имеющую вид:
. Тогда, используя соотношения (9), (10) и (12), получим
оценку, имеющую вид:
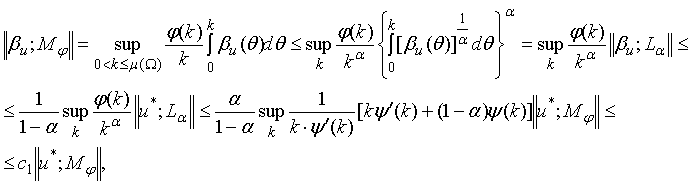 где
где 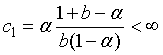 .►
.►
В
заключение, рассмотрим несколько особо характерных вход-выходных операторных
преобразований, имеющих многочисленные приложения в синтезе динамических интегральных
систем, (см. обзор [4]).
Нелинейные операторы, входящие в динамическую
интегральную модель – это, как правило:
а) нелинейный оператор
суперпозиции-Немыцкого
![]() ; (14)
; (14)
б) нелинейный интегральный оператор
Гаммерштейна:
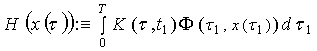 ; (15)
; (15)
в) нелинейный интегральный оператор Урысона:
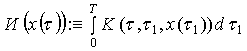 ;
(16)
;
(16)
г) оператор Лихтенштейна-Ляпунова:
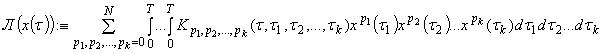 .(17)
.(17)
Естественно, не все нелинейные системы
поддаются описанию моделями с помощью операторов, связывающих в явном виде вход
системы с ее выходом. Если, например, в рассматриваемой нелинейной динамической
системе существует обратная связь, то эта система описывается операторным
уравнением вида:
![]() , (18)
, (18)
где В –
нелинейный оператор. Так, в динамических системах контроля и учета, являющихся
следящими, оператор В часто удается
представить в виде нелинейного интегрального Гаммерштейна Н.
Литература:
1. Miroshnik I.V.
Nonlinear and Adaptive Control of Complex Dynamical Systems / I.V. Miroshnik,
V.O. Nikiforov, A.L. Fradkov. St.-Petersburg: Nauka, 2000. 549 p. (Series
«Analysis and Design of Nonlinear Systems»).
2. Blondel V. Unsolved problems in
mathematical systems and control theory / V. Blondel, A. Megretski. Princeton
University Press, 2004. 334 p.
3. Przeworska-Rolewicz, D. Equations in
linear spaces / D. Przeworska-Rolewicz, S. Rolewicz. – Warszawa, 1968. – 380 p.
4.
Крылов В.В. Построение моделей
внутренней структуры динамических систем по входо-выходным соотношениям (теория
абстрактной реализации). I. Обзор / В.В. Крылов// Автоматика и телемеханика. 1984. № 2. С. 5-19.