Professor,
Shuakayev M. K., Ph.D. Nazarbekova
S.T., Shuakayeva A.
JSC "MMC Kazakhaltyn",
Republic of Kazakhstan,
Kazakh National University by named al Farabi, Republic of Kazakhstan, JSC "BTA Bank",
Republic of Kazakhstan
Stochastic Volterra`s Models of Control Systems for
Describing of Biological Systems
In this paper stochastic model of growing fungus is
presented, which is a 3-dimensional bilinear stochastic system and is managed
by 3 characteristics: temperature, moisture components and nutrition with
minerals. After that managing problems and managing initial system problems are
investigated, which helps to manage the process of fungus growth and by that
allows us to describe the model of a rather complicated technological process
in more details. New approach for control system development is also presented
in this paper.
Introduction
Investigators quite often analyze differential equation system for the
description of mathematical models of biological systems. This differential equation system does not
let manage the process, occurring in the biological system and gives accurate
information only at specific moments and for fixed characteristics. It is quite
difficult to trace the whole difficult technological process of growing fungus,
which requires the processing of input parameters of the system that are to be
effectively arranged by any means.
Process control system of growing fungus can be described with bilinear
stochastic system as follows:
![]() (1)
(1)
![]() (2)
(2)
where À and  – matrix with 3õ3 dimension, and w (t) is three
dimensional vector– column, with the following
data w1(t) – keeping a specific temperature, moisture w2(t) –and w3(t) – feeding with
mineral resources,
Ñ (.) – dimension vector n x 1, y
(.) – is called system’s output.
In case u (t) = 0 , then the system (1) determines an initial condition,
i.å. matrix À determines an initial condition in which initial data is input, which
included biological data of the object, environment temperature etc.
In this case the system’s parameter (1) has to be chosen so that matrix À is stable, i.e. its eigenvalues
lies on the left half-plane.
Example1. If matrix A represented
À= ![]() .
.
Then its
eigenvalues is defines by following equation
det (
A-![]() E ) = 0,
E ) = 0,
solving
it we obtain eigenvalues matrix A equally -2 and -1. Consequently matrix A is stable.
The equations (1) - (2) generalizes systems of cultivation of microbes from [4]. In
(1)-(2), matrix A defines specific growth rate
, matrix B – concentration of flowing into growth, input y(t) is the
same in [4].
For determination cross-correlation functions we formulate by following
theorem.
Theorem1. For the system (1) – (2) there is a Volterra`s model, for which the sequence of
relative correlation functions is determined by the
kernel of bilinear determined system [8], i.e. by the following:
![]() . (3)
. (3)
Then Hankel`s matrix H for system
(1) – (2) is chosen as follows:
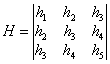 (4)
(4)
In this case for the successful appliance of algorithm of realization it
is obligatory to require its full range, i.e
(H) ≠ Î.
(5)
System (1) – (2) can be used for the description of mathematical models
for higher fungus and lower fungus as well.
Proof of this
theorem as follows by using Ito
formulas of Stochastic derivation we can exactly fined of sequence mutually
correlation functions and
after we obtain (3 – (5).
System (1) - (2)
can be used for describing
the mathematical models for both lower and higher types of
cultivation of microbes.
According to Theorem 1, the process
of constructing the Hankel`s matrix H, we can
conclude that the
deterministic controllability
matrix is defined as:
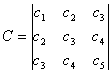 ,
(6)
,
(6)
where parameters
![]() ,
,
and the matrix of determined observation N is a three-dimensional matrix with parameters as follows:
![]() ,
(7)
,
(7)
Then
object (1) – (2) deterministically controlled, if conditions are as follows:
de t (Ñ) ≠ Î ,
(8)
and we obtained condition observeability, if
de t (N) ≠ Î ,
(9)
In this case Hankel`s matrix Í is determined as
follows:
Í
= Ñ ∙ N,
(10)
Condition (4) labels that the process of growing fungus is both
deterministically controlled and can be observed.
In our opinion complicated biological process of growing fungus which
was described shortly above, is to be investigated in effective system of data
handing. That’s why we developed the following subsystems: «cosmopolitan»,
«commonly occurring», «rare in occurring», «new for the area of research » and
«dominant».
However, data base is developed only for the major part of
«Cosmopolitan», subsystem and other subsystems: «commonly occurring», «rare in
occurring», «new for the area of research » and «dominant» are contained in it,
based on their similar qualities and for the data handing we also develop only
one system of data handing which is «Cosmopolitan».
In this paper working
outed Packet of Appling Program, including Control Systems Bases of Dates, Constraction Hankel matrixe, Woking
Out of Volterras model (series) and other subsystems.
Referents:
1. Assaubayev K.Sh.,
Shuakayev M.K. / Volterra series
and control theory. - Vol.1, Alma-Ata,1993,p.167.
2. Assaubayev K.Sh., Shuakayev M.K. /Algebras and liable groups. Volterra
series and control theory. Vol. 2, Almaty, 1993, p.187.
3. Assaubayev K.Sh., Shuakayev M.K. /Volterra series and control theory. - Vol.
3, Almaty, 1993, p.187.
4. Williamson D. / Observation of Bilinear Systems
with Application to biological Control// Automatica, vol.13, 1977, p.p.
243-254
5. Nazarbekova S.T,
Ashurov H., Mirzakhmedov Sh., Dalimov
D.N., Azizov S.T. The study of the role of some micromycetes in enzymatic
hydrolysis of the walls of seed crops little oil-bearing / Materials XI Congress of Russian Botanical
Society / / Botanical research in Asian Russia. Barnaul. 2003, Vol.1, p.p.
45-46
6. On the current state of lichen herbarium of Botany Department KazNU /
Development of plant science in Central Asia and its integration into the
production / / Proceedings of the International Conference. Tashkent. 2004.
S.280-282
7. Lebedev O.V., Ruban I.N., Voropayeva N.L., Nazarbekova S.T .The use of
information and nano-biotechnology for analysis, forecasting, and improving the
environmental situation in the area of oil
production in the Aral Sea and the Aral Sea / International
scientific-practical conference, .Schuchinsk. 2007. P.265-269
8. Bruni C., Di Pillo G. and Koch G. Bilinear systems: IEFF TR. Aut. Coutr.,
1974,p.p.334–348
9. Barab, A. -L.; Oltvai, Z. (2004). "Network
biology: understanding the cell's functional organization". Nature
reviews. Genetics 5 (2):
101–113.
10. Covert; Schilling, C.;
Palsson, B. (2001). "Regulation of gene expression in flux balance models
of metabolism". Journal of Theoretical Biology 213 (1): 73–88.
11.
Covert, M. W.; Palsson, B. . (2002). "Transcriptional regulation in
constraints-based metabolic models of Escherichia coli". The Journal of
Biological Chemistry 277
(31): 28058–28064.