К.ф.м.н., профессор, Кузьмичева А.Е., магистрант Коннов Ю.В.

Западно-Казахстанский государственный университет им. М. Утемисова,

г. Уральск, Казахстан

Научность, абстракция и идеализация

при решении физических задач.

Принцип научности является одним из основных дидактических принципов. Он предполагает «соответствие содержания образования уровню развития современной науки и техники, опыту, накопленному мировой цивилизацией» [1]. В соответствии с принципом научности в содержание образования входит ознакомление обучаемых с объективными научными фактами, явлениями, законами, формирования представлений о научной физической картине мира. Образовательные программы, определяемые ГОСО Республики Казахстан, «предусматривают изучение на современном уровне всех основных разделов физики, начиная от механики Ньютона и заканчивая физикой элементарных частиц» [2]. В них представлена система последовательного рассмотрения различных уровней структурной организации материи, их законов и закономерностей, описание природы и свойств объектов окружающего мира. Обращается внимание на модельный характер физических теорий и указание границ их применимости.

Реальные физические объекты, явления, процессы очень сложны вследствие многообразия причин и взаимных связей их определяющих. Поэтому в физической науке создаются модели, в той или иной мере соответствующие реальности. Понятие модели определяется различным образом. Одно из определений: «модель – это такой объект, изучение которого служит средством для получения знаний (информации) об исходном объекте, называемом прототипом или оригиналом» [3]. В целом модель определяет некоторые свойства физической системы и условия существования состояния или условия протекания процесса, явления. Построенная модель должна быть научной, объективно отражающей реальность. Например, в молекулярно-кинетической теории модель удовлетворяет трем известным условиям: система состоит из частиц, частицы хаотически двигаются и взаимодействуют между собой. В модели идеального газа взаимодействием частиц пренебрегается. Если движение частиц задается законом Ньютона, то модель классическая, если волновыми уравнениями – модель квантовая. В квантовой статистической физике к этим условиям добавляется указание на принадлежность частиц к классу фермионов или бозонов.

Построение модели, моделирование тесно связано с процессами абстрагирования и идеализации. Абстрагирование – это «мысленное отвлечение от ряда свойств предметов и отношений между ними и выделение, вычленение в изучаемом объекте какого-либо главного (наиболее значимого) свойства или отношения». Идеализация в физике – «процесс образования (создания) абстрактных объектов, принципиально не осуществимых в опыте и несуществующих в действительности» [3]. Идеальные объекты являются предельными по отношению к реальным. Выделяется три вида идеальных моделей:

- образные (рисунки, графики, схемы и т.п.)

- знаково-символические (уравнения, формулы)

- мысленные модели – научное представление о каком-либо явлении в форме его описания на естественном языке.

Использование моделей и моделирования решает проблему наглядности в познании и позволяет свести сложное к более простому.

Учебный материал физики группируется вокруг основных фундаментальных физических теорий, знание и понимание которых является требованием к обязательному (минимальному) уровню подготовки учащегося по предмету «физика». Учебные задачи – неотъемлемая часть процесса обучения. Необходимость и целесообразность их решения определены педагогической и методической наукой. Физические задачи разнообразны по содержанию, форме задания условия и требования и другим особенностям. Естественно, что они также должны удовлетворять принципу научности. При этом целесообразно обратить внимание на некоторые особенности реализации этого принципа в задачах:

- использование научных данных в содержании задач;

- учет границ применимости физических теорий в количественных характеристиках задач;

- возможные нарушения принципа научности в задачах при использовании методов абстрагирования и идеализации.

В физических задачах, содержащихся в многочисленных сборниках, пособиях, предлагаются различные задачные ситуации. Они могут относиться к абстрактным, отвлеченным понятиям: материальная точка движется…, тело вращается…, заряд находится в электрическом или магнитном поле… В ряде задач информация о ситуации конкретизируется: тело – автомобиль, заряд – электрон, протон, α-частица; магнитное поле в циклотроне и т.п. Решение таких задач расширяет знание обучаемых о физических характеристиках реальных систем.

Современный школьник находится в широком информационном поле. Много информации, в том числе количественной, он получает из различных источников. Роль учителя состоит в создании условий использования имеющихся знаний и мотивации к поиску дополнительной информации.

Рассмотрим несколько примеров:

1. Физические величины являются размерными, то есть имеют единицы измерения, с которыми выполняются математические операции как с числами. Характеристики могут быть даны в различных системах единиц измерения. Умение работать с единицами измерения – одно из требований. С целью активизации познавательной деятельности обучаемых можно предложить задачи, предполагающие использование различных источников, справочников…

- сравнить скорости самых быстрых и самых медленных животных;

- сравнить максимальные скорости самолетов или машин различных типов, марок;

- сравнить скорости самолетов в середине прошлого и начале нынешнего века.

Такие задачи создают мотивацию к изучению скоростных характеристик животного мира и технических объектов, к постановке вопроса о том, какие научные достижения позволяют существенно увеличить скорость. Аналогичные задачи можно составить на сравнении мощностей различных технических устройств.

В курсе электричества и магнетизма при решении задач важно использовать достижения современной науки по характеристикам электромагнитных полей в лазерах, ускорителях элементарных частиц, характеристики космического электромагнитного излучения, магнитных полей планет, звезд, межпланетного и межзвездного магнитных полей, температур различных объектов Вселенной и др. К поиску информации о таких характеристиках целесообразно привлечь самих обучаемых, что будет способствовать формированию их информационной компетентности. Знание достижений науки в количественных характеристиках физических объектов, явлений, процессов может быть использовано и при анализе правильности полученного результата.

2. Принципиальным при изучении специальной теории относительности Эйнштейна является вопрос о релятивистской массе, как массе зависящей от скорости, который с начала 90-х годов стал дискуссионным. В содержание физики школ РК входит формула зависимости массы от скорости и предлагается решение задач, в том числе и на Едином Национальном Тестировании в РК с использованием этой формулы. В то же время в государственных программах России усилиями ведущих ученых-физиков этот вопрос снят. Понятие массы, зависящей от скорости, изъято из школьных программ. Это понятие вводится только как характеристика частиц, инвариантная к преобразованиям Лоренца. С этой точки зрения фотон не имеет массы (вопрос о вычислении массы фотона так же входит в содержание тестовых вопросов ЕНТ). Поэтому при изучении физики в вузе и средней образовательной школе сложившаяся ситуация должна быть доведена до обучаемых. Они должны уметь выполнять требуемые расчеты, но понимать, что вопрос о релятивистской массе теоретически не однозначен. Если он остается в программах РК, значит среди ученых нет единого мнения по этому вопросу.

3. Принципиальным с научной точки зрения является вопрос о плотности Земли в задачах на расчет силы тяготения или ускорения свободного падения тела, находящегося внутри Земли, их зависимости от глубины. Рассмотрим несколько подобных задач:

а) Доказать, что сила тяготения, действующая на материальную точку массой m внутри Земли где R₀ - радиус Земли, r -расстояние точки от центра Земли, r < R₀ (плотность Земли считать постоянной) [4. № 7.6]

б) На какой глубине в единицах радиуса Земли ускорение свободного падения составляет 0,9 от ускорения свободного падения на поверхности Земли. Плотность Земли считать постоянной [5. № 5.21].

в) С какой силой притягивается к центру Земли тело массы m, находящееся в глубокой шахте, если расстояние от тела до центра Земли равно r? Постройте график зависимости силы притяжения от r. Плотность Земли считать одинаковой и равной p [6. № 242, 6, № 36].

г) Найти изменение ускорения силы тяжести при опускании тела на глубину h. На какой глубине ускорение силы тяжести составляет 25% от ускорения силы тяжести на поверхности Земли. Плотность Земли считать постоянной [7. №2.153].

В приведенных задачах предлагается выполнять решение в модели однородной Земли, то есть считать массу равномерно распределенной, плотность одинаковой во всех точках. В такой модели ускорение свободного падения:

g ~ r; или

Здесь r - расстояние от центра Земли, h - глубина, отсчитываемая от поверхности, R - радиус Земли, ρ - плотность, g₀ - ускорение свободного падения на поверхности Земли. Графически данная зависимость представлена на следующих рисунках:

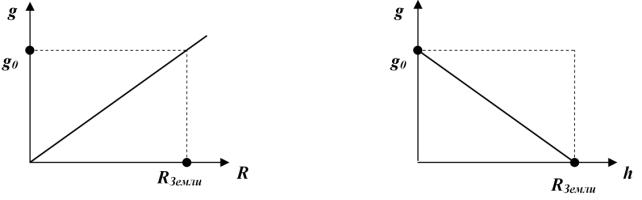
Насколько такая модель однородной плотности Земли не соответствует научным представлениям видно из сравнения с рисунками 6 и 7, приведенными в справочнике [7]

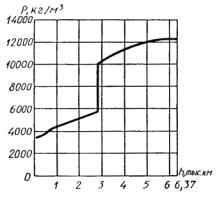
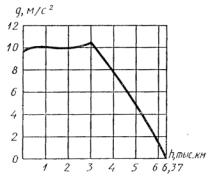
Рисунок 6 Рисунок 7

Из рисунка 6 видно, что модель однородной Земли сильно отличается от модели принятой в науке. Следствием реальной модели является приведенный на рисунке 7 график зависимости g от глубины h, из которого видно, что, начиная от поверхности и почти до половины расстояния от центра, оно почти не изменяется. Интересно отметить, что максимальное значение ускорения свободного падения оказывается не на поверхности Земли, а на глубине 2900 км.

Одна из целей обучения – формирование у обучаемых представлений о физической картине мира, в том числе о нашей Земле, ее внутренним строении, с которым связаны происходящие катастрофические события – землетрясения, извержения вулканов, цунами. Поэтому для современного человека важно понимание процессов внутри Земли и «навязывание» в задачах представлений об однородной Земле оказывается антинаучным.

4. Необходимость внимательного отношения к границам применимости теорий, моделей наглядно видна и в задачах на движение тел, брошенных под углом горизонту, на что обращено внимание в учебниках СОШ. Идеализация и абстрагирование в этих задачах, связанных с расчетом дальности полета при условии отсутствия сопротивления приводит к принципиальной погрешности в результатах. При решении задач важно так же учитывать границы применимости фундаментальных теорий и принятых моделей. Например, модель классического идеального газа применима только в определенном интервале температур и давлений. Поэтому, при составлении задач с использованием в условии или решении диаграмм изопроцессов (Р, Т), при V=const или (V, Т) при Р=const, линия графика не может доходить до начала координат. При низких температурах в модели идеального газа вместо известного распределения Максвелла-Больцмана используется распределение Ферми-Дирака для систем фермионов, или Бозе-Эйнштейна для систем бозонов. Такие примеры можно привести из различных разделов физики.

Таким образом, реализации принципа научности, условиям применимости абстракции и моделей, расширению представлений о научной картине мира, технических достижениях должно уделяться соответствующее внимание не только при изучении теории, но и на практических занятиях при решении физических задач.

Литература:

1. Сластенин В.А., Исаев И.Ф., Шиянов Е.Н. Педагогика 6-е изд. - М.: 2007. - 576 с.

2. Государственный общеобязательный стандарт образования Республики Казахстан. Начальное, основное среднее, общее среднее образование. 2.3.4.01-2010

3. Дамитов Б.К. Методика обучения решению физических задач. ЗКГУ, Уральск, 2002г., 216 с.

4. Гольдфарб Н.И. Задачник. Физика 9-11. М. «Высшая школа». 1992 г.

5. Турчина Н.В., Рудакова Л.И., Сурова О.И. и др. Физика: 3800 задач для школьников и поступающих в ВУЗы. М., «Дрофа», 2000.

6. Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараева И.М. Сборник задач по элементарной физике. Изд. «Наука», М., 1988 г.

7. Волькенштейн Е.С. Сборник задач по общему курсу физики. М. Наука, 1980 г.

8. Енохович А.С. справочник по физике. М. «Просвещение». 1990 г.