Математика и физика
Тұрбаев Б.Е., Парменова
М.Ж., Бегайдаров М.Т.
Қорқыт Ата
атындағы Қызылорда мемлекеттік университеті, Қазақстан
Республикасы
МАТЕМАТИКА МЕН
ФИЗИКАНЫ БАЙЛАНЫСТЫРА ОҚЫТУ ӘДІСТЕРІНІҢ ТИІМДІЛІГІ
Елбасымыз
Н.Ә.Назарбаевтың «Қазақстан-2050 стратегиясы –
қалыптасқан мемлекеттің жаңа саяси бағыты» атты
Жолдауы еліміздің ұзақ мерзімді дамуындағы жаңа
белестерді айқындайтын бағдарламалық тарихи маңызды
құжат болып табылады.
Еліміздің
жаңа даму бағытында білім беру жүйесінің алдында:
1.
Білім беру мекемелерін оңтайландыру;
2.
Оқу-тәрбие үдерісін түбегейлі жаңғырту;
3.
Білім беру қызметтерінің тиімділігін арттыру сияқты
үш басты бағыт айқын қойылды. Соның ішінде жалпы
білім беретін мектептердің алдында тұрған шұғыл
міндет – оқуды өмірге, жаңа технологияға жақындату.
Осыған байланысты мектептегі іргелі жаратылыстану-математика
бағытындағы пәндерді оқытудағы әдістемелік
мәселелердің мәні ерекше артады.
Мектептегі оқу үдерісінде математика мен
физиканы ұштастыра оқыту әдістерін қолдану
математикадан тиімді және терең, білім берудің
алғышарттарының бірі болып табылады. Математика мен физиканың
бұрынғыдан да тығыз байланыста қарастыру
қажеттілігі математиканың ерекше сипатынан, яғни оның
айрықша кең қолданысынан шығады.
Амал не, бүгінгі шындыққа келсек, ол мұғалімдердің
көпшілігінің математикадан сабақ беру іс-әрекетінде
математика мен физика арасындағы байланыс әлі де өзінің
тиісті орнын ала алмай келеді. Бұл оқушылардың физика
формулалары мен заңдарын функционалдық тәуелділік ретінде
қарастыра алмауы, фунция мен аргументтің, оң және теріс
сан мәндерінің физикалық мағынасын аша алмауы
дәлел бола алады.
Мұның барлығы осы кездегі математика пәні бойынша
қолданыстағы оқулықтарда физикалық мазмұнды
мысалдар мен жаттығулардың өте аздығы немесе кейбір
тақырыптар бойынша мүлде болмауынан түсіндіріледі.
Физика-техникалық
мазмұнды есептердің аздығы немесе болмауы, кездесетін
есептердің мақсатсыз шешілуі, функцияның үнемі тек 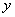 -пен, аргументтің
-пен, аргументтің 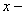 пен белгіленуі және сызықтық функцияның
жазылуы тұрақты
пен белгіленуі және сызықтық функцияның
жазылуы тұрақты 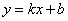 түрінде, ал
квадраттық функцияның
түрінде, ал
квадраттық функцияның 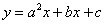 түрінде болуы,
графиктер салғанда осьтерінің барлық уақытта х пен у (х-горизонталь,
у-вертикаль) арқылы белгіленуі түптеп келгенде оқушыларда
өзгертуі қиын стереотиптің қалыптасуына алып келеді.
түрінде болуы,
графиктер салғанда осьтерінің барлық уақытта х пен у (х-горизонталь,
у-вертикаль) арқылы белгіленуі түптеп келгенде оқушыларда
өзгертуі қиын стереотиптің қалыптасуына алып келеді.
Осыдан
оқушылар санасында функциялық тәуелділік, функция
ұғымы 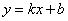 ;
; 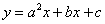 жазуларымен
байланыста, немесе функциялық тәуелділіктің
аналитикалық түрі тек х және у болғанда ғана туады.
жазуларымен
байланыста, немесе функциялық тәуелділіктің
аналитикалық түрі тек х және у болғанда ғана туады.
Бұндай
жағдайлардың барлығы математика сабақтарында физика-техникалық
есептерді пайдалануға жағдай жасамайтындығы түсінікті.
Сондықтан оқушылар жалпылама, жалаң мәлімет алады, ал
ол жылдам ұмытылады да, оның өзі кең тараған
техника мен жаратылыстану ғылымдарының көптеген
салаларының дамуына қажетті математиканың беделін кемітеді,
қызығушылықты төмендетеді.
Жоғарыда
айтылғандарға байланысты: қандай физикалық есептер
математика сабақтарында қандай мақсатпен қашан
және қалай шығарылуы керек деген сұрақ туады.
Бұл баяндамада біз физика есептерін математика сабақтарының
кейбір тақырыптарында қолданылуын қарастыруға талпынып
отырмыз. Алдымен абстрактілі математикалық өрнегімен салыстыруды
қарастырайық.
Абстрактілі
математикалық өрнектерді физика формулаларымен, олардың
графиктік белгіленуін, анықталу облысын және түрі бірдей
функция болуын айыра көрсету арқылы салыстырулар, математика
ережелерінің жалпылығын көрсетуде ерекше маңызды орын
алады. Мысалы 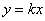 түріндегі
сызықты функция мен бірқалыпты қозғалыс теңдеуін
салыстыруды мынадай түрге келтіруге болады:
түріндегі
сызықты функция мен бірқалыпты қозғалыс теңдеуін
салыстыруды мынадай түрге келтіруге болады:
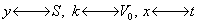
|
1. у-ті х-қа байланысты функция ретінде
қарастырамыз.
|
1. s-ті t-ға байланысты функция ретінде
қарастырамыз.
|
|
2. 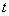 саны х айнымалысы
сияқты кез келген нақты мән қабылдай алады. саны х айнымалысы
сияқты кез келген нақты мән қабылдай алады.
|
2. Бірқалыпты қозғалыс кез
келген жылдамдықты ала алмайды.
|
|
3. Нақты мәселерге байланысты 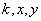 шамаларының
атаулары әртүрлі болуы мүмкін. шамаларының
атаулары әртүрлі болуы мүмкін.
|
3. Бұл жағдайда 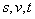 шамаларының
нақты атаулары бар. шамаларының
нақты атаулары бар.
|
|
4. Бұл функцияның графигі түзу
болады.
|
4.
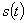 графигі жарты
түзу, себебі графигі жарты
түзу, себебі 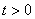 жағдайы қарастырылады. жағдайы қарастырылады.
|
Сонымен
физика формулалары белгілі шек қойылған функциялық
тәуелділік ретінде қарастырылады.
Осыған
ұқсас мысалдар оқушылардың абстрактілі
математикалық өрнекте нақтылы көруіне және
жекелеген нақты мысалдардан жалпы қорытынды шығаруға
көмектеседі.
Енді «Алгебра
және анализ бастамалары» пәні бойынша негізгі туынды және
интеграл амалдарына байланысты физика-техникалық мазмұнды
жаттығулардың нақты шешімдерін келтірейік.
1-мысал. Нүкте  параболасының
бойында уақытқа тәуелді
параболасының
бойында уақытқа тәуелді 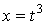 заңдылығымен қозғалады. осы
нүктенің ординатасы қандай жылдамдықпен өзгереді?
заңдылығымен қозғалады. осы
нүктенің ординатасы қандай жылдамдықпен өзгереді?
Шешуі: Туындының физиканың мағынасы
бойынша жылдамдық нүктенің координатасының уақыт
бойынша туындысы, яни 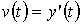 . Ал
. Ал 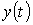 - күрделі
функция, оның туындысы
- күрделі
функция, оның туындысы 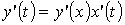 . Бұдан:
. Бұдан: 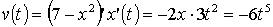 .
.
Жауабы: 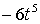 .
.
2-мысал. Жоғары тік лақтырылған дене 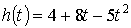 заңдылығымен қозғалады,
мұндағы
заңдылығымен қозғалады,
мұндағы 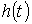 - метрмен
өлшенетін биіктік, ал
- метрмен
өлшенетін биіктік, ал 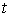 - секундпен
өлшенетін уақыт.
- секундпен
өлшенетін уақыт.
а)
дененің бастапқы жылдамдығын;
б) Жермен
түйіскендегі жылдамдығын;
в)
Көтерілудің ең үлкен биіктігін табыңыздар.
Шешуі: а) Дененің 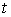 уақыт
моментіндегі жылдамдық
уақыт
моментіндегі жылдамдық 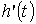 туындыға
тең, яғни
туындыға
тең, яғни 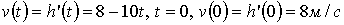
б) Жермен
түйіскенде 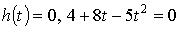 , бұдан
, бұдан 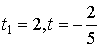 (мағынасы жоқ). Сонда
(мағынасы жоқ). Сонда 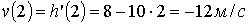 (минус таңбасы жылдамдықтың бастапқы
жылдамдыққа қарсы бағытталғанын көрсетеді.
(минус таңбасы жылдамдықтың бастапқы
жылдамдыққа қарсы бағытталғанын көрсетеді.
в) Ең
үлкен 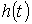 биіктікке
дененің жылдамдығы нольге тең болып, көтерілуден
төмен түсу кезеңінде жетеді; яғни
биіктікке
дененің жылдамдығы нольге тең болып, көтерілуден
төмен түсу кезеңінде жетеді; яғни 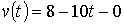 , бұдан
, бұдан 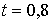 . Ең үлкен биіктік
. Ең үлкен биіктік 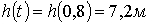 .
.
3-мысал. Тұрақты ток
өткізетін көлденең қимасынан уақыт бірлігінде
өтетін электр мөлшерімен анықталады. осыған
сәйкес айнымалы токқа анықтама беріңіздер. Өткізгіштен
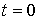 уақыт мезетінен
бастап өтетін ток мөлшері
уақыт мезетінен
бастап өтетін ток мөлшері 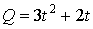 формуласымен берілсе,
бірінші секундтың соңындағы ток мөлшерін
табыңдар.
формуласымен берілсе,
бірінші секундтың соңындағы ток мөлшерін
табыңдар.
Шешуі. Уақыт өзгерісіне сай
электр өзгерісін табу үшін ток күші ұғымын
пайдаланамыз. 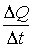 қатынасы
уақыттың
қатынасы
уақыттың 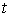 -дан
-дан 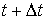 -ға дейінгі орташа ток күші деп аталады
және
-ға дейінгі орташа ток күші деп аталады
және 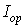 тұрақты
болады. Егер тізбекте айнымалы ток болса, онда
тұрақты
болады. Егер тізбекте айнымалы ток болса, онда 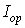 уақытқа
байланысты өзгеріп отырады. Сондықтан тізбектегі айнымалы ток
күші
уақытқа
байланысты өзгеріп отырады. Сондықтан тізбектегі айнымалы ток
күші 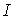 ұғымы
енгізіледі және оны
ұғымы
енгізіледі және оны 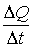 -ның
-ның 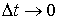 шегі ретінде
анықтайды.
шегі ретінде
анықтайды.
Сонымен 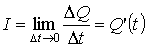 . Бұдан
. Бұдан 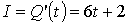 .
.
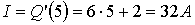 .
.
Жауабы: 32А.
4-мысал. 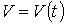 нүктесінің
нүктесінің 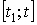 уақыт аралығындағы
түзу сызықты қозғалысының жылдамдығы
болсын.
уақыт аралығындағы
түзу сызықты қозғалысының жылдамдығы
болсын. 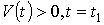 ден
ден 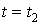 уақыт
аралығында нүктенің жүріп өткен жолы қалай
анықталады?
уақыт
аралығында нүктенің жүріп өткен жолы қалай
анықталады?
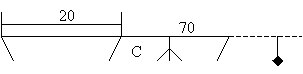

Шешуі: Қозғалып бара
жатқан нүктенің 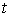 уақыт
мезетіндегі координаталарын
уақыт
мезетіндегі координаталарын 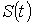 деп белгілейік.
деп белгілейік. 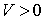 болғанда
жылдамдық тек оң бағытта болғандықтан (
болғанда
жылдамдық тек оң бағытта болғандықтан (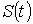 функциясы өспелі болады,
функциясы өспелі болады, 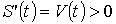 ) ізделінді қашықтық мына санмен беріледі:
) ізделінді қашықтық мына санмен беріледі: 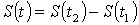 .
.
Екінші жағынан 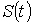 функциясы
функциясы 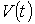 функциясының
алғашқы функциясы болғандықтан, жоғарыдағы
айырма
функциясының
алғашқы функциясы болғандықтан, жоғарыдағы
айырма
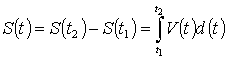
интегралын береді.
5-мысал. Массасы 5кг жүк белгілі
биіктіктен құлап келе жатыр және жердің бетіне 2,5
секундтан кейін келіп түседі. Жүктің жасаған
жұмысын табу керек.
Шешуі: Жүктің толық
жұмысы мынаған тең: 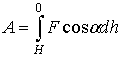 .
.
Мұндағы 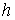 - жүк
құлай бастаған биіктік;
- жүк
құлай бастаған биіктік; 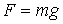 жүкке
әсер ететін ауырлық күші;
жүкке
әсер ететін ауырлық күші; 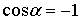 .
.
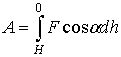
теңдеуді түрлендірсек:
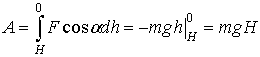
мұндағы 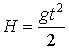 болғандықтан,
болғандықтан,
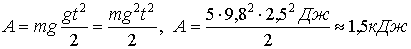
Жауабы: 1,5кДж.
6-мысал.
Вертикаль плотина тең бүйірлі трапецияға
ұқсас. жоғары табаны төменгі табанынан ұзындау.
жоғарғысының ұзындығы – 70м, төменгісінің
ұзындығы – 50м, биіктігі – 20м. Плотинаға қандай
қысым әсер етеді?
Шешуі:
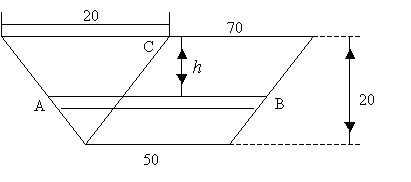

АВ
сызығы 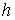 тереңдікте
орналасқан. Оның ұзындығы СВ кесіндісі мен АС
кесіндісінің қосындысынан тұрады. АВ оның
ұзындығы
тереңдікте
орналасқан. Оның ұзындығы СВ кесіндісі мен АС
кесіндісінің қосындысынан тұрады. АВ оның
ұзындығы 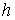 тереңдігінен
тәуелді. Үшбұрыштар ұқсастығынан
тереңдігінен
тәуелді. Үшбұрыштар ұқсастығынан 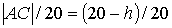 , сондықтан
, сондықтан 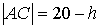 , ал АВ-ның ені
, ал АВ-ның ені 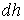 -қа тең. бұдан
-қа тең. бұдан 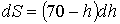 және
және 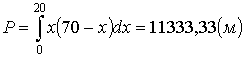
7-мысал. Өзенге салынған су плотинасы кіші осі
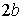 су бетінде жататын
жарты эллипс формасында. Эллипстің үлкен осі -
су бетінде жататын
жарты эллипс формасында. Эллипстің үлкен осі - 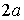 . Судың плотинаға түсіретін қысымын
анықтау керек.
. Судың плотинаға түсіретін қысымын
анықтау керек.
Егер су
плотинасына сай эллипстің осьтерін 17-суреттегідей орналастырсақ,
онда оның теңдеуі 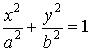 болады.
болады.
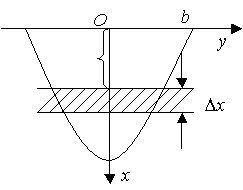

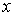 тереңдікте ені
тереңдікте ені 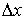 болатын жолақты
қарастырайық. Бұл жолақтың ауданы
болатын жолақты
қарастырайық. Бұл жолақтың ауданы 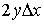 табамыз.
табамыз. 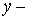 тің шамасын эллипстің теңдеуінен табамыз.
Судың меншікті салмағы
тің шамасын эллипстің теңдеуінен табамыз.
Судың меншікті салмағы 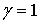 деп аламыз.
деп аламыз.
Сұйыққа
вертикаль батырылған дененың қабырғаларына
түсетін қысым күші 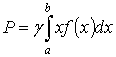 болатыны физикадан
белгілі.
болатыны физикадан
белгілі.
Сонда
қысымның шамасы 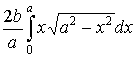 . Анықталған интегралды есептеу арқылы
. Анықталған интегралды есептеу арқылы 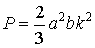 болатын сандық
мәнін аламыз.
болатын сандық
мәнін аламыз.
Әдебиеттер:
1.
Әбілқасымова А.Е., Шойынбеков К.Д., Есенова М.И.,
Жұмағұлова З.А., «Алгебра және анализ бастамалары»,
10-сынып, Алматы, «Мектеп», 2006.
2.
Әбілқасымова А.Е., Бекбоев И.Б., Абдиев А.А.,
Жұмағұлова З.Ә., «Алгебра және анализ
бастамалары», 11-сынып, Алматы, «Мектеп», 2007.
3.
Гурский И.П. Элементарная физика с примерами решения задач. –М.: Наука,
1989, -464с
![]() -пен, аргументтің
-пен, аргументтің ![]() пен белгіленуі және сызықтық функцияның
жазылуы тұрақты
пен белгіленуі және сызықтық функцияның
жазылуы тұрақты ![]() түрінде, ал
квадраттық функцияның
түрінде, ал
квадраттық функцияның ![]() түрінде болуы,
графиктер салғанда осьтерінің барлық уақытта х пен у (х-горизонталь,
у-вертикаль) арқылы белгіленуі түптеп келгенде оқушыларда
өзгертуі қиын стереотиптің қалыптасуына алып келеді.
түрінде болуы,
графиктер салғанда осьтерінің барлық уақытта х пен у (х-горизонталь,
у-вертикаль) арқылы белгіленуі түптеп келгенде оқушыларда
өзгертуі қиын стереотиптің қалыптасуына алып келеді. ![]() ;
; ![]() жазуларымен
байланыста, немесе функциялық тәуелділіктің
аналитикалық түрі тек х және у болғанда ғана туады.
жазуларымен
байланыста, немесе функциялық тәуелділіктің
аналитикалық түрі тек х және у болғанда ғана туады.![]() түріндегі
сызықты функция мен бірқалыпты қозғалыс теңдеуін
салыстыруды мынадай түрге келтіруге болады:
түріндегі
сызықты функция мен бірқалыпты қозғалыс теңдеуін
салыстыруды мынадай түрге келтіруге болады:![]()
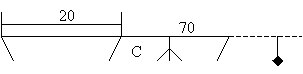

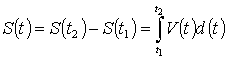
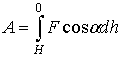 .
.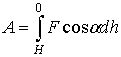
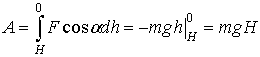


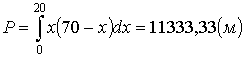
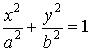


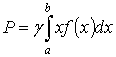
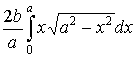 . Анықталған интегралды есептеу арқылы
. Анықталған интегралды есептеу арқылы