Педагогические науки/5. Современные методы преподавания

К. п. н., доцент А.И. Азевич

ГБОУ ВПО Московский городской педагогический университет

Институт математики и информатики

Дидактические возможности программы GeoGebra в обучении математике

Современное программное обеспечение коренным образом меняет качество уроков математики. Они становятся интереснее, познавательнее и динамичнее. Сейчас уже трудно представить себе преподавание без интерактивных моделей, наглядно и последовательно открывающих ученикам мир разнообразных знаний!

Один из способов накопления демонстрационного материала для уроков – создание интерактивных апплетов. Апплеты – это небольшие приложения (часть документа HTML), размещаемые в Интернете. Они могут запускаться пользователем с сайта преподавателя. Кроме того, файлы сохраняются с расширением .ggb и в любой момент могут быть использованы на уроке. Перед их запуском, надо установить на компьютер программу GeoGebra и научиться конструировать нужные апплеты. По сути апплет – это мини-программа, созданная на языке Java.

Какие дидактические возможности открывает учителю интерактивная среда Geogebra? Прежде всего, она служит для подготовки наглядных учебных моделей: графиков функций, геометрических чертежей, таблиц, диаграмм. Бесспорные достоинства программы – свободное распространение, кроссплатформенность, русский интерфейс, простота использования и широкое многообразие функций.

Geogebra незаменима на уроках алгебры, геометрии, статистики. Чтобы оценить ее преимущества, подготовим несколько апплетов. Например, для урока алгебры 7-го класса по теме «График линейной функции». Как известно, линейная функция – это зависимость, задаваемая формулой y=ax+b.

Изучая тему, ученик знакомится с определением функции и алгоритмом построения графика в системе координат. Он должен знать, как меняется положение прямой в зависимости от значений параметров a и b. На этом этапе обучения будет полезен апплет, подготовленный в программе GeoGebra. Он наглядно покажет движение прямой на плоскости.

Как подготовить такой апплет? Довольно просто. Буквально в несколько шагов! Создаем два ползунка a и b, нажав на соответствующую кнопку панели задач. В окне объектов программы появляются две папки: свободные объекты и зависимые объекты. Следующий шаг: в строку ввода записываем формулу y=ax+b. Нажимаем Enter. На рисунке появляется прямая. Ползунок запускает перемещение прямой на плоскости. Если двигаем ползунок а, прямая вращается вокруг точки (0, а). Если работает ползунок b, она совершает параллельные переносы вдоль оси OY. За прямой можно закрепить название и некоторую фиксированную точку (рис.1). Чтобы имя прямой двигалось вместе с ней, надо вызвать функцию «Надпись» и в открывшемся окне вставить "Прямая 1: " + l_1. У прямой появится обозначение , а соответствующая формула будет непрерывно следовать за ней.

Рис.1

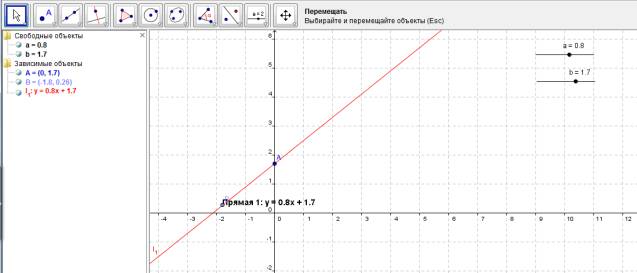
Данный пример свидетельствует об уникальных дидактических возможностях программы. Интерактивная и динамичная модель графика помогает ученикам лучше понять свойства линейной функции.

Приведем еще один пример, теперь уже из геометрии. В нем будет показан способ построения связных геометрических фигур, а также ход создания новый команды. Предположим учителю надо объяснить построение окружности, вписанной в треугольник. Перед тем, как это сделать, стоит провести с учениками эвристическую беседу. Она приведет к понятию окружности, вписанной в треугольник. Затем обозначить учебную проблему: «Как найти центр описанной окружности и ее радиус?» Ход обсуждения сопровождается построениями в программе GeoGebra. Параллельно создается новая команда, которая в дальнейшем может быть использована ни на одном уроке геометрии.

Итак, чтобы построить окружность, вписанную в треугольник, а заодно и добавить новую команду, выполним последовательность действий.

1. Построим треугольник.
2. Проведем биссектрисы его углов.
3. Отметим точку D пересечения биссектрис.
4. Спрячем биссектрисы, используя панель объектов.
5. Опустим перпендикуляр из точки пересечения биссектрис на одну из сторон треугольника. Отметим основание перпендикуляра Е и спрячем его, вновь используя панель объектов.
6. Построим окружность, проходящую через точки D и Е (О – ее центр, Е – точка на окружности).
7. Отметим точки касания окружности со сторонами треугольника.
8. Инструменты – Создать инструмент – Входные объекты (выбрать из списка или нажать на вершины треугольника) – Входные объекты (окружность и ее центр).
9. Имя и значок. Вписанная окружность. Описание: «Отметьте три вершины треугольника». Рисунок значка приготовить заранее.

10. Нажать на кнопку «Завершить». В окне появится новая команда, которой можно воспользоваться, если потребуется окружность, вписанная в треугольник (рис.2).

Рис.2

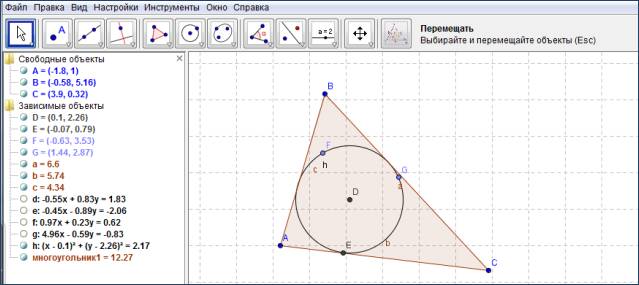
Нетрудно убедиться, что чертеж опять получился динамичным. Для этого достаточно потянуть за одну из вершин фигуры. Форма и размеры треугольника изменятся, но окружность останется «привязанной» к треугольнику.

Объяснив ученику, как подготовить апплет, можно дать на дом практическое задание. Оно будет состоять из нескольких пунктов. Скачать программу GeoGebra. Установить ее на компьютер и, пользуясь предложенными алгоритмами, подготовить апплеты. При этом надо изменить название функции (1 пример) и характер расположения геометрических объектов (2 пример). Подобную работу желательно проводить с учениками чаще. На уроках математики вводятся новые функции, новые геометрические фигуры, новые задания. Живая, практическая деятельность формирует у учеников прочные умения и навыки. Им интересно конструировать собственные апплеты с помощью программы GeoGebra. А демонстрация готовых мини-программ не только повышает интерес к предмету, но и формирует исследовательский подход к решению задач.

В Интернете немало готовых апплетов, сделанных сторонниками программы GeoGebra. Математики со всего мира обмениваются уникальными работами, которые могут быть использованы учителем на уроке. При этом дидактическая ценность такого интерактивного урока возрастает многократно!