Разживин В.М., Воскресенский А.В.

Пензенский государственный университет архитектуры и строительства,

г..Пенза.(Россия)

ОСОБЕННОСТИ ИЗОЛЯЦИИ ВОЗДУШНОГО ШУМА ЛЕГКИМИ ОГРАЖДЕНИЯМИ

Звукоизолирующая способность ограждающих конструкций определяется не только поверхностной плотностью и частотой звука, но и линейными размерами изолирующей поверхности, потерями на внутреннее трение в материале ограждения, характеристиками примыкающих (сопрягаемых) элементов. Каждый из этих факторов по-своему оказывает влияние на изоляцию воздушного шума и, разрабатывая инженерные методы расчета, необходимо принимать во внимание результаты действия каждого из них.

В практике строительства имеют место два способа закрепления легких ограждений, при которых выполняется либо заделка посредством защемления или сварки при использования листовых материалов, либо закрепление посредством упругих прокладок и защемления, обеспечивающих одновременно прочность обжатия и герметичность соединения. В формировании колебаний ограждающими конструкциями принимают участие вынужденные и свободные волны. Вынужденные волны определяются уровнем звукового давления в падающей волн, а свободные – величиной отражения от краев. Таким образом, при одних и тех же условиях воздействия диффузного звукового поля наблюдается разница в изоляции воздушного шума в зависимости от граничных условий.

Известна возможность построения физических моделей, позволяющих объяснить снижение изоляции при упругом закреплении краев в сравнении с жестким. Определяющим условием выбора модели является отсутствие или наличие волнового движения в исследуемых конструкциях.

Тело, в котором проявляется волновое движение или укладывается более 1/6 длины волны, предложено представлять в виде приведенной массы. Величина приведенной массы определяется как 1/2π массы тела, охваченного волновым движением за один период колебаний и для реальной конструкции

(например, пластины при воздействии звуковой волны) подсчитывается по формуле:

μ_i = [ b х h х ρ х с_и,п] / ( 2π g х f_i) ( 1 )

где μ_i – приведенная масса i- й ограждающей конструкции;

b , h , ρ – соответственно ширина, толщина и плотность материала рассматриваемого элемента;

с_и/п- изгибная скорость в пластине или массивной примыкающей конструкции и, соответственно, продольная скорость распространения волны в материале упругого элемента;

g , f _i– ускорение свободного падения и текущая частота.

Таким образом, в отличии от элементарных моделей типа «сосредоточенная масса- сосредоточенная упругость», приведенные массы учитывают в полной мере физические и геометрические характеристики рассматриваемых тел с учетом частоты колебаний и изменяющимися расчетными схемами. Рассмотрим каждый из способов закрепления.

а) жесткое закрепление краев ограждения (рис.1).

Рис.1.Модель жесткого закрепления.

Расчетная модель представляется упругим ударом приведенных масс ограждения и примыкающей конструкции. Результат взаимодействия может быть описан уравнениями, одно из которых выражает закон сохранения количества движения, а второе – сохранения кинетической энергии:

μ _пл = μ_пл х β + μ_пр.к х α ; ( 1 )

(μ_пл х 1²) / 2 =(μ_пл х β²) /2 + (μ_пр.к х α²) / 2 ( 2 )

Решение этой системы позволяет получить значения коэффициентов прохождения α и отражения колебательной скорости β пластины:

α = 2 μ_пл / (μ_пл+ μ_пр.к) ; β = (μ_пл- μ_пр.к) / (μ_пл+ μ_пр.к) ( 3 )

б)упругое закрепление краев ограждения (рис.2).

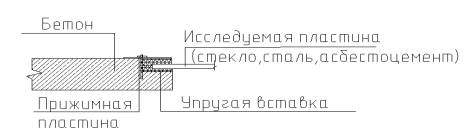
Рис.2.Модель упругого закрепления.

Расчетной моделью служит колебательная система типа «приведенная масса - упругость – приведенная масса», трансформирующаяся после появления волнового движения в упругой прокладке в модель упругого удара приведенных масс пластины, прокладки и примыкающей.

Частота, начиная с которой в прокладке толщиной h проявляется

волновое движение при прохождении продольной волны С_пр, рассчитывается по формуле :

f _пр = С_пр / 6 h ( 4 )

Если до начала волнового процесса в упругой прокладке на частотах первая модель описывается зависимостью

R_i = 20lg ׀1-( f_i/f₀)²׀ ( 5)

из которой коэффициент отражения определяется по формуле

β = ( 1 – 0,1^{0,1 х Ri} )^0,5 ( 6)

то величина коэффициента отражения колебательной скорости второй модели для двухкаскадной системы рассчитывается по формуле

β= β₁ х β₂

где β₁ и β₂ вычисляются по ф.3 с соответствующими индексами;

f₀ – частота собственных колебаний системы.

Величина снижения изоляции воздушного шума легкими ограждениями в зависимости от условий закрепления краев может быть определена следующим выражением:

Δ L_i = 10 lg (1/ m ) х [1/(1 – a ^m х β) х (1/(1 – a ^0.5) ] -5,4 дБ ( 7)

где m – количество полуволн изгиба, укладывающихся по длине элемента на рассматриваемой резонансной частоте;

β– коэффициент отражения колебательной скорости от краев ограждения;

а=е ^{–π х η} - затухание колебания на одну длину волны при коэффициенте потерь η .

Результаты работы подтверждают имеющееся на практике снижение изоляции воздушного шума легкими ограждениями, которое не учитывалось ранее в подобных расчетах.

ЛИТЕРАТУРА

1.Ковригин С.Д., Захаров А.В., Герасимов А.И. Борьба с шумом в гражданских зданиях. – М., Стройиздат,1969.