Строительство и архитектура / 7. Водоснабжение и канализация
К.т.н. Калякин А.М., Чеснокова
Е.В., Сауткина Т.Н.
Саратовский
государственный технический университет
имени Гагарина Ю.А., Россия
Особенности кинематики потока со
сдвигом перед цилиндром на твердом основании.
Решение уравнений движения
приближенным
способом.
Часть 3
В части 1 решалась задача о выборе зависимости
для ![]() и
и ![]() , в части 2 был выполнен анализ различных формул для
составляющей
, в части 2 был выполнен анализ различных формул для
составляющей ![]() .
.
В первых двух частях использовалось уравнение
неразрывности, а в данной части решаются уравнения движения вязкой жидкости
(ламинарный режим).
Ниже излагается один из возможных способов
использования уравнений движения для уточнения ранее полученных зависимостей
для ![]() ,
, ![]() ,
, ![]() .
.
Имея выражения для составляющих скорости ![]() ,
, ![]() ,
, ![]() в данном случае можно
при разнообразном выборе
в данном случае можно
при разнообразном выборе ![]() ,
, ![]() и
и ![]() подобрать такие корректирующие функции
подобрать такие корректирующие функции ![]() ,
, ![]() и
и ![]() , чтобы составляющие действительной скорости в каждой точке
представлялись по формулам
, чтобы составляющие действительной скорости в каждой точке
представлялись по формулам
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
В любой точке рассматриваемой области каждую из
функций ![]() ,
,![]() и
и ![]() можно разложить в ряд
(например, ряд Тейлора) по трем переменным
можно разложить в ряд
(например, ряд Тейлора) по трем переменным ![]() ,
,![]() и
и ![]() :
:
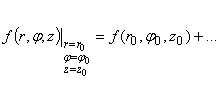 (4)
(4)
и
использовать разложение типа (4) для подстановки в (1)-(3). Полученные таким
образом зависимости (1)-(3) подставляются в уравнение Навье-Стокса (или в
уравнение движения в иной форме) и определяются функции ![]() ,
, ![]() и
и ![]() [1].
[1].
В первом приближении разложение (4) в точке
можно принять равным ![]() , т.е. ограничиваемся первым членом.
, т.е. ограничиваемся первым членом.
Поэтому положим
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
После подставления (5)-(7) в уравнение
Навье-Стокса получаем систему алгебраических уравнений относительно трех
неизвестных ![]() ,
, ![]() ,
, ![]() , принимающих различные значения в разных точках
рассматриваемой области.
, принимающих различные значения в разных точках
рассматриваемой области.
Для распределения давления по оси ![]() можно принять [2]
можно принять [2]
![]() (8)
(8)
И использовать дополнительно уравнение
неразрывности.
Заметим, что найденные таким образом величины ![]() ,
,![]() и т.д. не будут вполне определять знак (а, следовательно, и
физический смысл)
и т.д. не будут вполне определять знак (а, следовательно, и
физический смысл) ![]() ,
, ![]() ,
, ![]() , так как знак первого члена разложения в данной точке не
обязательно совпадет со знаком численного значения функции в данной точке.
, так как знак первого члена разложения в данной точке не
обязательно совпадет со знаком численного значения функции в данной точке.
Уравнения Навье-Стокса в цилиндрических
координатах имеют вид (не делается никаких ограничений) [3].
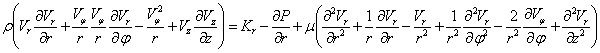 (9)
(9)
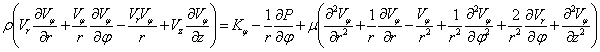 (10)
(10)
![]() (11)
(11)
Уравнение неразрывности имеет вид:
![]() (12)
(12)
Уравнения Эйлера имеют вид
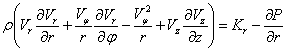 (13)
(13)
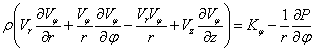 (14)
(14)
![]() (15)
(15)
Рассмотрим
применение предложенного способа на примере уравнений Навье-Стокса.
Прежде всего вычисляем значение всех величин,
входящих в эти уравнения (для составляющей ![]() принята форма,
соответствующая первому из четырех рассмотренных вариантов):
принята форма,
соответствующая первому из четырех рассмотренных вариантов):
![]() ;
; ![]() ;
;
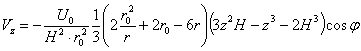 ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; 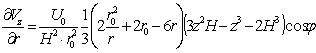 ;
;
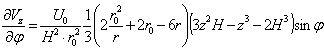 ;
; 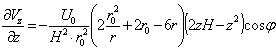 ;
;
![]() ;
; 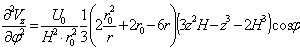 ;
;
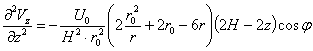 ;
; ![]()
Обозначим в данном случае ![]() ,
, ![]() ,
, ![]() .
.
И в силу (5)-(7),
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
тогда
все остальные соотношения можно обозначить следующим образом:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Теперь не трудно найти величины со штрихами
(дифференцируя (16)-(18)):
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Все вышенаписанные
величины со штрихами необходимо затем подставить в уравнения движения (уравнения
Навье-Стокса) – в результате получится система линейных уравнений относительно
постоянных коэффициентов. Заметим, что предлагаемый подход не лишен
недостатков, в частности, если бы в разложении (4) учитывать вторые члены, то неизвестных
было бы в 2 раза больше. А вторые считают, что полученные в первом приближении
результаты могут быть полезными в качестве первого шага к изучению данного явления.
Литература
1.
Березин И.С., Жидков Н.П. Методы вычислений. Т. II. Гос. изд-во физ.-мат.
литературы. М.: 1960 г.-620 с.
2.
Милн-Томсон Л. Теоретическая гидродинамика. М.: Мир, 1964 г.-660 с.
3.
Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа. 2003 г.-840с.