Грешнов А.Ю.
Национальный университет
кораблестроения им. адм. Макарова, Украина
Оптимальное соотношение диаметров проводников
коаксиального чувствительного элемента полиметрической информационно –
измерительной системы
При
использовании полиметрических методов один измерительный преобразователь должен
обеспечивать одновременное измерение нескольких величин, отражающих состояние
контролируемой жидкой среды [1].
Задачи импульсной
полиметрии - излучение специальным образом сформированного зондирующего сигнала
в измерительный преобразователь специальной
конструкции, который погружен в контролируемую среду; прием соответствующего
полиметрического сигнала, его обработка и интерпретация (оценка качественных и
количественных параметров контролируемой жидкой среды) [2].
Один из путей развития
информационно – измерительных систем состоит в разработке методов и средств, позволяющих
значительно расширить функциональные возможности чувствительных элементов (ЧЭ)
путем их «полиметризации», т.е. обеспечения возможности одновременного измерения
ряда физических величин одним измерительным преобразователем.
В идеальном случае
такой ЧЭ должен иметь возможность одновременно оценивать механические,
физические, химические и др. величины,
комплексно отражающие состояния контролируемого
объекта, т. е. быть системным.
Значение точной величины
волнового сопротивления коаксиального ЧЭ необходимо при проведении
полиметрических измерений [3].
Волновое сопротивление
данного ЧЭ определяется выражением:
где 
– относительная
диэлектрическая проницаемость жидкой среды; 
– внутренний диаметр
наружного проводника; 
– диаметр внутреннего
проводника.
При конструировании
коаксиального ЧЭ необходимо в первую очередь выбрать диаметры внутреннего и
внешнего проводников и установить их в наивыгоднейшее соотношение. Затухание
коаксиального ЧЭ может быть определено по следующей формуле (без учета потерь в
диэлектрике):
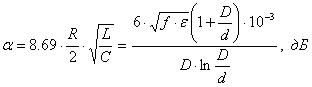
где 
– полное активное
сопротивление коаксиального датчика, 
; 
– емкость датчика, 
; 
– индуктивность
датчика, 
; 
– частота тока,
.
Выразим отношение 
через 
. Из данного выражения следует, что с увеличением 
его числитель растет
линейно, а знаменатель возрастает по логарифмическому закону. Исследовав данную
формулу на минимум затухания в зависимости от 
(
), получим, что 
минимально при
соотношении 
. Таким образом, оптимальная конструкция ЧЭ будет иметь место
при 
. Это соотношение справедливо для ЧЭ с одинаковыми
проводниками. Если проводники изготовлены из различных металлов, то минимальное
затухание определяется из выражения:
;
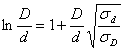где 
и 
– проводимости
металлов внутреннего и внешнего проводников.
Целесообразно выбирать
внутренний и внешний проводники из одинакового материала, имеющее малое
погонное сопротивление.
Нарушение оптимального
соотношения в меньшую сторону связано с резким возрастанием затухания. Поэтому
в ряде случаев целесообразно принять отношение 
больше оптимального.
При изготовлении коаксиального ЧЭ приходится также отступать от оптимального
соотношения 
, если волновое сопротивление датчика строго нормировано
(например, W=75 Ом). В этом случае отношение 
определяется по
формуле:
.
Литература:
1.Датчики: Справочное
пособие / [Гордеев Б.Н., Жуков Ю.Д., Шарапов В.М., Полищук Е.С, Ишанин Г.Г.,
Гуржий А.Н., Викулин, И.М., Кошевой Н.Д., Курмашев Ш.Д., Куценко А.Н., Марченко
С.В., Минаев И.Г., Совлуков А.С.] –
Черкассы: Брама-Украина, 2008. – 1072 с.
2.
Жуков Ю.Д. Контактная
сверхширокополосная локация в системах оперативного контроля качества и
количества жидких энергоносителей / Ю.Д. Жуков, Б.Н. Гордеев // Вісник Черкаського
державного технологічного університету. –
2006. – Спецвипуск. – С. 141 –
143.
3.
Гордєєв Б.М. Конструктивні особливості чутливих елементів коаксиального типу
поліметричних систем / Б.М. Гордєєв, А.Ю. Грешнов // Науково-методичний журнал
чорноморського Державного університету iм. Петра Могили. – 2011. – Т. 163. Вип. 151 – С.44 – 49.