Л. Т. КУРБАНАЛИЕВ
кандидат физико-математических наук МКТУ им. Х.А.Ясави
Г.А.ДУЙСЕНОВА
преподаватель МКТУ им. Х.А.Ясави
Е.З.УКСИКБАЕВ
магистрант МКТУ им. Х.А.Ясави
Решение задачи колебания приповерхностного слоя анизотропной
слоистой среды методом потенциалов
В
работах [1,2] рассмотрена задача колебании приповерхностного
слоя анизатропного слоистой среды. Состояние слоистой среды
описывалось моделью линейной упругости [1]. Предположим, что на
подошву слоя падает одномерная поперечная упругая волна (рис. 1). Будем
учитывать отражение и преломление поперечной волны от границ слоев ( рис.
2).
Н
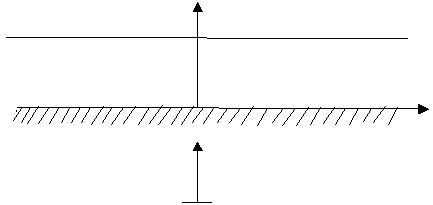

поперечная волна
Рисунок 1. Падающая упругая
одномерная поперечная волна.
переломанные волны отраженные волны
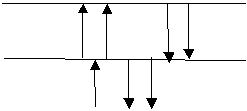

поперечная волна
отраженные волны
Рисунок 2. Схематическое
изображение волн.
Граничные условия:
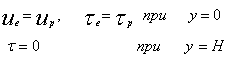 (1)
(1)
Начальные условия:
![]() (2)
(2)
Потенциал падающей волны
представим в виде:
![]() (3)
(3)
Тогда потенциалы отраженных и переломных волн можно представит
в виде:
![]()
(4)
![]()
где b0, b, b1 - скорости
падающей, отраженных и преломленных поперечных волн соответственно;
B0,B, Bp - амплитуды падающей, отраженных и преломленных
поперечных волн;
![]() - потенциалы падающей,
отраженных и преломленных поперечных волн;
- потенциалы падающей,
отраженных и преломленных поперечных волн;
В работе [2]
приводятся выражения для
поперечных и продольных волн:
![]() (5)
(5)
Из
соотношения получим :
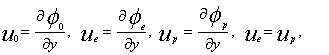 (6)
(6)
где ![]() - перемещения
падающей, отраженных и переломленных волн
соответственно. Причем
- перемещения
падающей, отраженных и переломленных волн
соответственно. Причем ![]()
![]() , тогда находим производные по координате y:
, тогда находим производные по координате y:
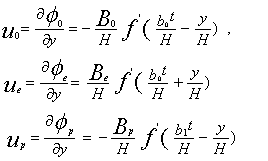 (7)
(7)
Компоненты тензора деформации и напряжении в упругом
случае выражаются через компонентов перемещений в виде [2,3]:
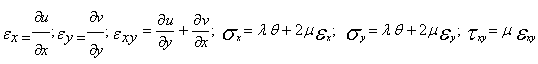
(8)
Исходя из постановки задачи и учитывая (8) имеем:
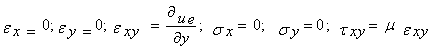 (9)
(9)
Находим выражение для компонентов ![]() и
и ![]() :
:
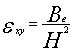
![]()
![]() ;
; 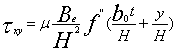
Уравнение колебания слоя:
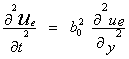 (10)
(10)
В работе [2] показано, что уравнение (10) в
потенциалах имеет вид:
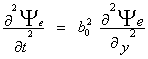 (11)
(11)
Перепишем граничные и начальные условия задачи в
потенциалах:
![]()
![]()
![]() (12)
(12)
![]() (13)
(13)
Полупространство
и слои характеризуется скоростями попереченых волн b0, b1,
коэффициентами Ляме ![]() и
плотностями
и
плотностями ![]() .
Нулевой индекс относится к
полупространству, а единичный к слою.
.
Нулевой индекс относится к
полупространству, а единичный к слою.
Скорости продольных и
поперечных волн выражаются через коэффициентами
Ляме и плотностями в следуюшем виде:
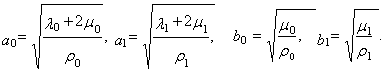
Можно вычислить
коэффициенты отражения продольных и поперечных волн [1]:
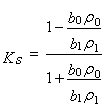 ,
, 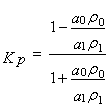 ,
,
где KS
, KP коэффициенты отражения поперечных и продольных волн.
Задачу (11) - (13) можно решить различными численными методами
[4]. Один из
методов, это конечно – разностный метод. В этом методе граничные,
начальные условия и уравнение движения записываются в конечно-разностной
схемой. В результате получим
систему линейных алгебраических уравнений (СЛАУ). Полученная СЛАУ решается
методом Гаусса или методом прогонки [5].
Другой метод численного решение задачу (11) - (13) метод Рунге-Кутта. Метод
Рунге-Кутта имеет порядок погрешности вычисления выше, чем
остальные численные методы [4].
ЛИТЕРАТУРА
1.
Григорян
С.С. Об основных представлениях динамики грунтов. – Прикладная математика и механика, 1960г., Т.24, выпуск №6, с.
1057-1072.
2.
Кольский
Г. Волны напряжения в твердом теле. М.:Мир, 1955г. - 150с.
3.
Самуль
В.И. Основы теории упругости и
пластичности. М.:Высшая школа, 1970. 120с.
4. Калиткин Н.Н.
Численные методы. М.:Наука, 1978. -120с.
5. Форсайт Дж.,
Моллер к. Численное решение систем линейных алгебраических уравнений. М.: Мир,
1969. – 250с.