Математика /1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Сяський В.А.

Национальный университет водного хозяйства и природопользования

Определение порядка сингулярности решения

одного класса интегральных уравнений

В работе [1] определение напряженного состояния бесконечной изотропной пластинки с круговым отверстием, подкрепленным на участке L₁=[-α₀, α₀] (α₀<π) тонким упругим стержнем, обладающим жесткостями на растяжении и изгиб, в условиях обобщенного плоского напряженного состояния сведено к системе двух сингулярных интегральных уравнений относительно контактных усилий T_ρ и S_ρλ, которую в комплексной форме можно представить следующим образом:

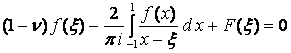. (1)

Здесь f(ξ)= T_ρ(ξ)+i S_ρλ(ξ), ν – коэффициент Пуассона материала пластинки; F(ξ) – непрерывная по ξ на отрезке [-1; 1] функция, удовлетворяющая условию Гельдера, содержащая функции T_ρ и S_ρλ под знаком определенных интегралов на промежутках интегрирования [-α₀, α₀], [λ, α₀], где λ=2arctga₀ξ, .

В классических контактных задачах линейной теории упругости особенности, присущие контактным напряжениям на концах участков соприкосновения упругих тел, имеют, вообще говоря, вид квадратного корня. Оказывается, что особенности такого же типа присущи усилиям T_ρ и S_ρλ рассматриваемой задачи. Для доказательства этого факта воспользуемся результатами работы [2].

Пусть плотность интеграла типа Коши

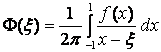(2)

в окрестности одного из концов -1 или 1, который обозначим через с, представима в виде:

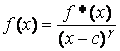
, ), (3)

где f*(x) – функция, удовлетворяющая в окрестности с условию Гельдера. Тогда для [-1; 1] справедливо представление [2]:

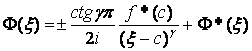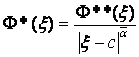
, . (4)

Здесь верхний знак берется при с=-1, а нижний – при с=1, а функция Ф**(ξ) удовлетворяет условию Гельдера в близи с (включая с).

Так как потенциальная энергия, накопленная в упругой пластинке в результате деформации, должна быть величиной конечной, то возможные особенности контактных усилий T_ρ и S_ρλ на концах подкрепляющего стержня должны быть интегрируемого порядка. Сказанное позволяет утверждать, что искомые контактные усилия можно представить в виде

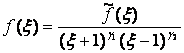, , (5)

где – непрерывная по ξ на отрезке [-1; 1] функция, удовлетворяющая условию Гельдера.

Для определения значений γ_j последнюю формулу запишем в виде

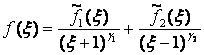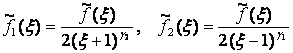; . (6)

Очевидно, что функции и соответственно в окрестностях точек ξ=-1 и ξ=1 удовлетворяет условию Гельдера.

Принимая во внимание (4) и (6), уравнение (1) представляем в виде

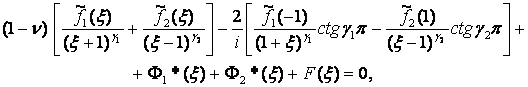(7)

где функции Ф₁*(ξ) и Ф₂*(ξ), согласно (4), обладают свойствами

, (8)

Очевидно, что этими свойствами обладает и функция F(ξ).

Умножая равенство (7) сначала на , а потом на и перейдя к пределу при и соответственно, получим следующие трансцендентные уравнения:

, . (9)

Решив их, определяем

, ; , . (10)

Таким образом, контактные усилия вдоль участка соединения стержня с пластиной имеют вид

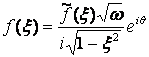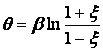; . (11)

Отделяя в (11) действительную и мнимую части, находим

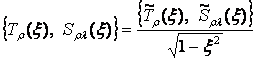, (12)

где – ограниченные на [-1; 1] функции.

Соотношение (12) показывает, что решение уравнения (1) следует искать в классе неограниченных на концах отрезка [-1; 1] функций.

Литература:

1. Сяський В.А. Напряженное состояние кусочно-однородной пластинки с инородным дуговым включением // Гидромелиорация и гидротехническое строительство. Львов: Изд-во Львов. ун-та . – 1984. – №12. – С. 115-119.

2. Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: Наука, 1968. – 511 с.