А. Д. Болычевцев, Н. А. Любимова, А. А. Чурсин

Украинская инженерно-педагогическая академия

АППРОКСИМАЦИЯ КВАНТОВАННЫХ СЛУЧАЙНЫХ СИГНАЛОВ ПО СОВОКУПНОСТИ ДИСКРЕТНЫХ ОТСЧЕТОВ

Проблема аппроксимации непрерывных сигналов (функций времени) по совокупности дискретных отсчетов имеет богатую методологическую родословную. Своими корнями она уходит в известную теорему В. А. Котельникова об адекватности непрерывной и дискретной форм представления информации, содержащейся в сигналах со строго ограниченным спектром [1]. Непрерывные случайные процессы имеют неограниченный спектр и не подпадают под эту категорию функций. Однако операторы импульсной модуляции приложимы и к ним, если удовлетвориться не полным, а приближенным соответствием информации, содержащейся в непрерывной и решетчатой функциях.

Учитывая медленную сходимость ряда Котельникова, восстановление непрерывных сигналов по совокупности дискретных отсчетов в реальной практике осуществляется не этим рядом, а какими-либо известными функциями времени, именуемыми воспроизводящими функциями. Предпочтение отдается полиномам как наиболее изученному классу математических объектов. При этом исходные и воспроизводящие функции рассматриваются как элементы функционального нормированного пространства, что позволяет ввести понятие «расстояния» между ними и говорить о качестве аппроксимации («близости» одной функции к другой).

В большинстве выполненных исследований по аппроксимации рассматривается идеализированный случай – точных измерений. Современные же технические средства позволяют измерять сигналы лишь с ограниченной точностью. Операция квантования по уровню является неотъемлемым компонентом первичной обработки воспринимаемого сигнала.

В результате квантования и дискретизации исходный непрерывный сигнал подлежит восстановлению по его дискретным, но уже не точным, а квантованным отсчетам. Это отражается на погрешности воспроизводящих его приближений. Поэтому при выборе шага дискретизации, учитывается совместное влияние обоих факторов – квантования и дискретизации.

В большинстве таких публикаций, как и в «классическом» варианте задачи, «близость» исходного и восстановленного сигналов оценивается разностью между ними – так называемой методической погрешностью. Задавшись каким-либо показателем этой погрешности (максимальное значение, средний квадрат и т.п.), можно поставить задачу о необходимой частоте дискретных измерений исходного сигнала. Однако такое решение, основанное на критерии «близости», экономически неоправдано: качество аппроксимации оказывается тем выше, чем меньше шаг дискретизации.

Предлагается ввести в рассмотрение вероятностный критерий качества дискретного измерения, понимая под ним вероятность того, что результаты произвольной пары соседних отсчетов отличаются друг от друга на один квант (цену делений измерительного прибора). В этом критерии признак «близости» сочетается с признаком «информативности», что позволяет, используя его в качестве критерия оптимальности измерительной системы, наилучшим образом согласовать интервалы квантования и дискретизации.

Пусть восстановлению по дискретным отсчетам подлежит какая-либо реализация нормального стационарного дифференцируемого в среднеквадратичном случайного процесса x(t) с дисперсией s² и нормированной корреляционной функцией r(t). Пусть Dt – шаг дискретизации процесса, а Dx – шаг его квантования. В этих обозначениях с точностью до относительной погрешности, не превосходящей 0.5%, вероятностный критерий качества p= p(Dx, Dt) выражается простой функциональной зависимостью [2]

p(Dx, Dt) = F(3s) – F(s), (1)

в которой F(z) – интеграл вероятности вида [3, 4]

F(z) = 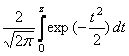, (2)

а s – некоторый обобщенный параметр дискретного измерения, связывающий вероятностные характеристики процесса s и r(t) с параметрами его квантования Dx и дискретизации Dt следующей зависимостью

s =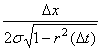. (3)

Как функция параметра s, вероятностный критерий (1) имеет экстремум (максимум) в точке s = s₀ = = 0.524. Значение экстремума

p₀ = p(Dx, Dt₀) = 0.484.

Это значит, что, при оптимальной равномерной дискретизации процесса x(t), примерно половина (48.4%) всех дискретных отсчетов будут отличаться от смежных с ними на один квант Dx.

Трактуя с этих позиций очередной отсчет как бинарное сообщение: отличен он (отсчет) или нет на один квант, – оценим количество информации I, содержащееся в таком сообщении. Согласно формуле Шеннона [1],

I = – p× log₂ p – (1– p) × log₂ (1– p).

В частности, при p = p₀ количество информации I = I₀ = 0.999 весьма близко к своему предельному значению – единице.

Уместно подчеркнуть слабую выраженность максимума вероятностного критерия (1). Так, при изменении обобщенного параметра s в окрестности точки оптимума s₀ на ± 10% значение критерия p(Dx, Dt) меняется менее, чем на 1%. Это показывает, что с точки зрения оптимизации измерительной системы существует довольно широкий интервал примерно равноценных значений шага дискретизации Dt.

Положив в (3) s = s₀ = 0.524, найдем

r(Dt₀) = . (4)

Зависимость (4) позволяет непосредственно на графике нормированной корреляционной функции измеряемого процесса получить оптимальное значение шага Dt₀. Для процессов с непрерывно дифференцируемыми реализациями [4, 5] можно использовать более простую – линейную зависимость, связывающую оптимальное значение шага дискретизации Dt₀ процесса с шагом его квантования Dx в явном виде

Dt₀ = 0.95,

w – усредненная круговая частота процесса.

Выше было установлено, что при оптимальном шаге дискретизации измеряемого процесса 48.4% отсчетов отличаются от смежных с ними на один квант. Можно показать, что оставшиеся 51.6% распределятся следующим образом: 39.9% отсчетов не будут отличаться от отсчетов, смежных с ними; 10.7% будут отличаться от смежных отсчетов на два кванта. А на смежные пары, отличающиеся на три и более кванта, приходится менее 1%. Отсюда следует, что при полиномиальном восстановлении исходного случайного процесса по совокупности его дискретных отсчетов достаточна ступенчатая или линейная интерполяция.

Литература

1. Кузьмин И. В., Кедрус В. А. основы теории информации и кодирования. – К.: Вища школа, 1986. – 240 с.

2. Болычевцев А. Д. Оптимальная дискретизация квантованных по уровню случайных сигналов // Автометрия. – 1973. – № 1. – С. 32-40.

3. Бронштейн И. С., Семендяев К.А. Справочник по математике. – М.: Наука, 1968. – 608 с.

4. Вентцель Е. С. Теория вероятностей. – М.: Наука, 1969. – 576 с.

5. Крамер Г., Лидбеттер М. Стационарные случайные процессы. – М.: Мир, 1969. – 398 с.