Oleg B. Malikov

Ph.Dr., professor, St.Petersburg State Transport University

METHODS of WAREHOUSE STOCK DETERMINATION

Abstract

The problem of stock determination at warehouses is very important for supply chains projecting and management. Usually the problem is searched theoretically while considering some supply chains which contain several warehouses with their stock. These researches mostly are concerned only supplying warehouses, although there are many other types of warehouses in supplying chains. Besides there are practical tasks, connecting with warehouse activity of cargo handling and stocks fluctuation. These procedures significantly influence on efficiency of work both – transport and warehouses and the whole supply chains. Their projecting sometimes is underestimated and considered as very simple procedure. Some methods of taking into account of the warehouse stock changing while warehouses projecting. are displayed in this article.

Keywords: Logistic Chain, Warehouse, Stock, Material flow, Unevenness, Cargo, Capacity, Probability, Transport

1. Introduction

Sometimes warehouse stock is considered as the most important problem in supply chains management. But before management of some system such as supply chain it is necessary to create this system i.e. it should be firstly projected, organized or its facilities should be built and put into action. It is not enough for this to know some constant level of warehouse stock, because material flows coming into and out of warehouses can change from day to day. So the warehouse stock is changed also. Under these conditions it is very difficult to project warehouse and particularly to determine warehouse dimensions, handling equipment and capacity.

However all main parameters of a warehouse and whole investments on its building and operation costs significantly depend on the level of the stock, keeping in it. And this stock level should be of some specific value.

2. The simplest methods

Nowadays warehouse stock in projecting more often is calculated on base of regular terms of stock keeping at warehouse. These terms were established on foundation of real experience of warehouses operation in different industries. With this method the warehouse capacity is computed as follows:

E=, (1)

where Q – annual value of material flow (in tones, units or m³);

t - term of stock keeping at the warehouse.

Drawback of this method is constant value of capacity, that does not take into account real conditions of changing of the warehouse stock during its activity/.

In real condition of warehouse operation the quantity stock is a some function of time and parameters of material flow going in Q₁ and out of the warehouse Q₂ :

I = f (t, Q₁, Q₂ ). (2)

So as changing of material flows, connecting with warehouse, are some stochastic processes, warehouse stock is also an unknown stochastic process. But warehouse dimensions and capacity are constant valuables for every specific warehouse. This contradiction can be overcome with special methods of warehouse stock calculation.

As was displayed in the Warehouse System Theory, developed in scientific works and books of the author [1, 2, 3], a warehouse should be considered as a technical system, i.e. as a complex of interconnected elements, created for reaching of united objective. The purpose of warehouse is transformation of material flows, that are going through it, with the least spending of 6 main resources – space, time, materials, labor, energy and money. This transformation is fulfilled for provision the most efficient further transportation or using of cargo. Temporary keeping and management of the merchandise stock are some part of technological operations, executed for this transformation of material flows.

So the warehouse system can be characterized with capacity E of its main storage area, additional capacity ΔE of its other areas (reception-dispatching areas, loading-unloading docks etc.) and real quantity of merchandise I, remaining at the moment at the warehouse.

Interaction of these valuables for supplying and transferring warehouses is shown in Figure 1. The difference between these warehouses is the purpose of their activity. The supplying warehouse should keep some insurance stock I₀ , that must provide supplying of consumers in case of interruption of cargo arrival to the warehouse.

a) b)

I I

ΔE ΔE

E E

I₀

0 Time 0 Time

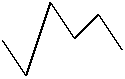
Figure 1. Interaction of stock fluctuating I and constant values capacity of storage area E and additional capacity ∆E of other areas for supplying warehouse (a) and transferring warehouses at long-distance transport (b)

For both these types of warehouses the stocks are fluctuating between two levels, but these levels are different for these ones. In supplying warehouse the stock fluctuates from insurance stock I₀ to the warehouse storage area capacity E (and sometimes up to additional capacity some other areas ∆E). In transferring warehouse the stock fluctuates from 0 to the warehouse storage area capacity E (and sometimes up to additional capacity some other areas).

Therefore in The Theory of Scientific Inventory Management several two-level methods of stock management were developed. The consideration of these methods goes over the limits of this article.

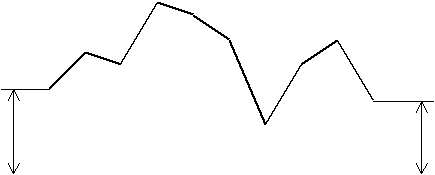
Function of warehouse stock, depending on time t I = f (t ) for constant time steps (for example – days) can be represented in form of polygon as shown in Figure 2.

I

Stock

I₀

T I_k

Time

1 2 3 4 5 6 . . . . . . k

Figure 2. Polygon of warehouse stock function I = f (t) as depending on time

While researching way of warehouse stock transformation, the warehouse is considered as some “black box”, which configuration is unknown and only its changing under influence of two flows – going in and out of the warehouse - are taking into account. This process can be described with function I = f (t ). Having integrated this function by time it is possible to determine the whole quantity of cargo W, that was kept at the warehouse for some period T.

However type of this function usually is unknown. Therefore the value W can be calculated with assistance of polygon of function, shown in Figure 2. In this case in is convenient to ust formulas of trapezium:

W = (3)

where Δt – value of time interval;

I₀ and I_k –respectively initial and finish values of warehouse stock;

k – number of time intervals (for example days, weeks or months).

Then average warehouse stock:

I= (4)

where T – the whole time of consideration.

Now the average time of cargo remaining at the warehouse:

τ = or τ = (5,6)

where λ - average intensiveness of cargo arrival to the warehouse.

3.Probability methods

There are several methods of warehouse capacity determination, that taking into account casual processes of arrival and dispatching of material flows from warehouse.

It is possible to calculate warehouse capacity as Mathematic Expectation M (I) of warehouse stock I:

E = M(I) = , (7)

where I_i - i-value of warehouse stock during time of stock research;

P_i - conforming Probability of i-value appearance;

n - the whole number of considering values of warehouse stock.

For using this method probability distribution of the warehouse stock should be created firstly, that can be fulfilled on the statistic base:

I = I₁ I₂ . . . I_n

P₁ P₂ . . . P_n , (8)

where I₁ I₂ . . . I_n - statistic election of warehouse stock in a warehouse, simi

lar to that under consideration;

P₁ P₂ . . . P_n - conforming probabilities of these stock values, that can be calculated with using of number of days in which the relative stock value has been observed:

P₁ = , P₂ = , . . . , P_n = . (9)

Other method of warehouse stock and capacity determination is one with assistance of Creditable Probabili. In this case the warehouse capacity is calculated not as one specific value, but as only possible value with creditable possibility p, for example 0,95 or 0,97. Other cases of 0,05 or 0,03 probability are considered as very rare and therefore they can be neglected.

For this method using also as in the previous case probability distribution of the warehouse stock should be produced, as mentioned above.

For the warehouse stock determination it is necessary to know the law of distribution of the stock :

F(I) = (10)

In Figure 3 an example is shown of warehouse stock determination for creditable possibility P=0.95.

Probability

1.0

0.9

0.8

0.7

0.6 F(I)

0.5

0.4

0.3

0.2

0.1 Stock I

Figure 3. Graph of warehouse stock distribution cumulative function F(I) with an example of stock determination for creditable probability P=0.95

4. New method of the warehouse stock and capacity determination

This method of warehouse capacity was created at Petersburg State Transport University and used while projecting a lot of warehouses for various industries. It can be called “In-Out Flows Combination” and does not require to form graph of distribution F(I) and contains only mathematic calculations. So it is possible to fulfill this method on computer and optimize capacity of warehouse with taking into account casual fluctuations of going in and out material flows.

The following probability distributions should be designated as initial data:

of arriving flow: Q_a = Q_a1 Q_a2 … Q_an ;

P_a1 P_a2 … P_an (11)

of dispatching flow: Q_d = Q_d1 Q_d2 … Q_dm

P_d1 P_d2 … P_dm . (12)

The core of this method is calculation of warehouse capacity as casual i-event, that is represented combination of probable values of flows going in Q_a and out of the warehouse Q_d:

I_i = I₀ + Q_ia – Q_id , (13)

where I₀ - is some initial or insurance stock, that is set depending on type of warehouse and some other conditions.

Probability of i-stock at the warehouse is calculated with formula:

P (I = I_i ) = P (Q_ai )* P (Q_di ), i = , (14)

where P (Q_ai ) and P (Q_di ) - conforming probabilities, that Q_ai cargo would arrive to the warehouse and Q_di cargo would be dispatched from the warehouse;

n – number of values in the flow going into the warehouse;

m - number of values in the flow going out of the warehouse.

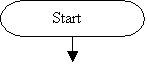
Block-chart of algorithm of the warehouse capacity calculation by this method for designated Creditable probability “p” is shown in Figure 4.

Delete number of considered value

Initial Stock

Next minimum

of stock

1 20 19

2 15 Yes

Looking for

minimum

1^st combination

of two flows

18

No

3 14 17

Sum of stock

probabilities ∑P_i

Initial probability

of stock = 0

1^st value of arrival

1^st finding of

minimum

1^st value

of dispatch

4 13

5 12 16

Probability

of i-case

6 No 21

Probability stock

11

Yes

7

Next value

of dispatching

10

Next value

of arriving flow

22

9

Next case

of flows

8 No

Yes

Figure 5. Algorithm of the method of stock calculation using material flows probability combination

Calculation of warehouse capacity with the mentioned method under simple conditions (when n and m are not more than 3-4) can be easily produced just on-hand, that is confirmed by the following example.

Let accept that it is necessary to determine capacity for a warehouse, that experienced the following material flows:

arriving flow: Q_a = 120 150 200

0.20 0.60 0.20 ; (15)

dispatching flow: Q_d = 140 180

0.65 0.35 , (16)

where 120, 150, 200 - number of transport batches (railway cars, trucks etc.), that

arrive to the warehouse for some period of time;

0.20, 0.60, 0.20 – conforming probabilities of these arriving quantities;

140, 180 - number of transport batches, that dispatch from the warehouse

from the same period of time;

0.65, 0.35 - conforming probabilities of these dispatching quantities.

Let us determine initial stock from the condition, that the warehouse was not empty at the beginning:

I₀ = 180 – 120 = 60 batches,

where 180 and 120 – minimal values relative arriving and dispatching flows into and out of the warehouse.

Assign the creditable probability of the stock calculation p = 0,95.

Let us calculate all the possible unions of arriving and dispatching material flows (there may be only 3*2 = 6 such combinations in the case):

1^st combination: Stock = 60+20-140=40;

probability of the stock: P(I=40)=0.20*0.65=0.13;

2nd combination: Stock = 60+20-180= 0;

probability of the stock: P(I=0)=0.20*0.35=0.07;

3rd combination: Stock = 60+150-140=70;

probability of the stock: P(I=70)=0.60*0.65=0.39;

4th combination: Stock = 60+150-180=30;

probability of the stock: P(I=30)=0.60*0.35=0.21;

5th combination: Stock = 60+200-140=120;

probability of the stock: P(I=120)=0.20*0.65=0.13;

6th combination: Stock = 60+200-180=80;

probability of the stock: P(I=180)=0.20*0.35=0.07.

It is necessary to verify that these cases form full group of events (in this case the sum of their probabilities must be equal 1.00):

= 0.13+0.07+0.39+0.21+0.13+ 0.07 = 1.00.

The standard condition is observed.

Thus probability distribution of warehouse stock as cooperation of two fluctuating flows has been formed:

Q_a = 0 30 40 70 80 120

0.07 0.21 0.13 0.39 0.07 0.13 .

Now the cumulative function of stock distribution (from less stock up to the bigger ones) can be produced:

I . . . . . . . . . . . . 0 30 40 70 80 120

F(I) . . . . . . . . . . 0.07 0.28 0.41 0.80 0.87 1.00.

From this function it can be seen that creditable probability having been assigned as p=0.95 is located between 0.87 (for stock 80 batches) and 1.00 (for stock 120 batches):

0.95 .

So design value of warehouse capacity may be determined in interval of possible stock E with the formula of linear interpolation:

E= = 105 transport batches.

5. Using the Queue Theory for warehouse capacity determination

With using of the Queue Theory methods the warehouse capacity may be determinated without preliminary gathering statistics and formation of probability distributions. But the drawback of these methods is calculation with some average values.

The author used the mathematic model of “destroying & multiplying” to produce a method of warehouse capacity determination with assistance of The Queue Theory.

In this case a warehouse is considered as many-channel mass-service system, with a place for keeping of cargo representing a canal of service of one transport batch (cargo from a truck or a railway car). “Refusal” is an event when the storage area is completely full and there is no room for reception next transport batch, which is considered as entry, that needs to be serviced, i.e. unloaded, received and put to the place of storage.

The process of entry service is considered as keeping merchandise in warehouse during some time τ, so that intensiveness of entry flow:

µ = 1/τ. (17)

The storage area can be in one of the following states W_i (see Figure 6):

W₀ – no place in the warehouse is occupied, i.e. the warehouse is empty;

W₁ – there is one transport batch in the warehouse;

W₂ - there are two transport batches in the warehouse;

W₃ – there are three transport batches in the warehouse;

. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . .

W_k - there are k transport batches in the warehouse (k places are occupied, other n-k places

are empty);

W_n - there are n transport batches in the warehouse (all the n places are occupied, no places

are empty);

λ λ λ λ λ λ

…… …….

µ 2µ 3µ kµ (k+1)µ nµ

Figure 6. Marked graph of states and transitions of the warehouse system relative its storage area occupation

From every states to another one in direction of increasing its stock (to the right in the Figure) the warehouse system transfers with intensiveness of λ in the moment, when the next transport batch comes into its storage area. So the system occurs in the (i+1) state.

Transition the warehouse system in direction of decreasing its stock (i.e. to the left in the Figure 7, from the i-state to the (i-1)-state) is happened with intensiveness of kµ in the moment, when a new transport batch is dispatched from the warehouse.

In according with the Queue Theory probability of storage area to be empty may be calculated with formula:

P(W₀) = 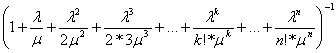(18)

or with taking into account expression (17):

P(W₀) = , (19)

where λ - intensiveness of the entering flow.

Probability of only one transport batch at the warehouse (k=1):

P(W₁) = => P(W₁) = λτ* P(W₀); (20)

Probability of two transport batches at the warehouse (k=2):

P(W₂) = => P(W₂) = (21)

Probability of k transport batches at the warehouse (k<n):

P(W_k) = => P(W_k) = (22)

Probability of n transport batches at the warehouse, i.e. when the storage area of the warehouse will be completely occupied:

P(W_n) = = > P(W_n) = . (23)

Now it is possible to determine probability of the storage area to be full not completely and next transport batch can be received into the warehouse:

P (k< n) = 1 - . (24)

Having designated average stock of cargo at the warehouse I = λ τ, it is possible the expression of probability of empty storage area rewrite in the following view:

P (W₀ ) = 1/ 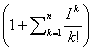. (25)

Then probability that there will be some room for cargo at the warehouse (24):

P(k<n) = 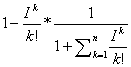. (26)

Changing the row, that is divider in this formula to e^I according to research of Macloren , receive probability of empty warehouse:

P (W₀ ) = = > P (W₀ ) = e^-I . (27)

Now the formulas (22) and (24) may be written in the following view:

Probability of k transport batches at the warehouse (k<n):

P (W_k ) = ; (28)

Probability that the storage area is not full completely and there is room for the

next transport batch to be received into the warehouse:

P (k<n) = . (29)

P(W_i )

0.270 k=2

0.250

0.200 0.169 k=6

0.150 k=10

0.124

0.100 0.086 k=20

0.050

k

5 10 15 20 25 30

Figure 8. Character of probability of having room for cargo at a warehouse P(W_i ) as depending on number of transport batches k at the warehouse at the moment

Distributions of occupying storage area of the warehouse as calculating by the formula (29) are displayed in Figure 8. It can be seen from this picture that average stock at the warehouse I = λτ conforms to the most probable stock and shows vertexes of the graph curves. However the stock may be exceeded and in this case capacity of the storage area would occur to be not enough.

For practical using this new method of capacity warehouse determination, the graphs of cumulative functions of stock distribution were produced which are shown in Figure 9. The graphs were formed with the following formula:

F (W_k ) = . (30)

F(W_k )

1.00

p=0.95

I=8,N=1460

I=4,N=730 I=10,N=1825

0.50

I=20,N=3650

k

5 10 15 20 25

Figure 9. Graphs of Cumulative Function of warehouse capacity distribution F(W_k ) as depending on transport batches number k for transferring warehouse with average term of cargo keeping 2 days (example is shown of warehouse capacity determination for capacity I=10 batches, annual flow N=1825 batches and creditable probability p=0.95)

6. Warehouse capacity determination by way of simulation

The task of determination of warehouse stock and capacity can be resolved by way of simulation on computer, but for this it is necessary to have special program, that is rather expensive (as a matter of fact under Russian conditions). Simulation of warehouse stocks provides possibility to determine them rather precisely.

Although for that it is also necessary to know the laws of material flows distributions – arriving to the warehouse and dispatching out of it. These laws are to be formed in the same manner as in methods of using probabilities.

The algorithm is based on the continuance equation:

Q₁ – Q₂ = (17)

where Q₁ , Q₂ - arriving and dispatching quantities of cargo;

ΔI – changing of the warehouse stock;

Δ t – period of time, for which the stock has changed by value of ΔI.

So initial data for simulation include laws of material flow going in and out of the warehouse and number of simulation experiences n. The flows can be assigned in view of tables, probability distribution or formula.

While simulation is in process, the warehouse stock the laws of casual quantities of arriving and dispatching cargo are formed with assistance of pseudo-casual numbers, evenly distributed in the interval [0,1] and on the foundation of assigned statistic distributions of material flows.

The computer program, having created values of in-going quantity of cargo Q₁ and out-going quantity Q₂ in every i-cycle of simulation experience calculates the warehouse stock as follows:

I_i = I_i-1 + Q₁ – Q_{2 ,} (18)

where I_i-1 - the warehouse stock in the previous, (i-1)-cycle of simulation experiences, that for the first cycle of simulation is taken equal to safe stock for a supplying warehouse and can be taken equal to 0 for a transferring warehouse at long-distance transport.

The number of experiences should be big enough (for example – 365 days, i.e. one year), so that the results received statistical steadiness and with determine probability could be acknowledged to be true.

Such simulation model was worked out at the Freight&Logistics Department of Petersburg State Transport University. In is displayed in Figure 10

.

* GPSS - Inventory Management

*********************************************************************

* *

* Order Point Inventory System *

* *

*********************************************************************

* Initialize and define

INITIAL X$ACB,150 ;Arrival Cargo Batch.

INITIAL X$Point,300 ;Order point

INITIAL X$Stock,1000 ;Set initial stock = 1000

Inventory TABLE X$Stock,300,50,7 ;Table of stock levels

Sales TABLE P$Demand,70,10,7 ;Table of dispatches per day

Var2 VARIABLE RN1@24+40

*********************************************************************

GENERATE ,,,1

Again TEST L X$Stock,X$Point ;Test of stock level

ADVANCE 1 ;Skip over time of 1 day

SAVEVALUE Stock+,X$ACB ;Addition to Stock

TRANSFER ,Again ;Repeat of stock replenishment

*********************************************************************

GENERATE 1 ;Create daily dispatch

ASSIGN Demand,V$Var2 ;Assign daily dispatch

TABULATE Inventory ;Record inventory

TEST GE X$Stock,P$Demand ;Make sure order can be executed

SAVEVALUE Stock-,P$Demand ;Remove cargo from stock

SAVEVALUE Sold,P$Demand ;X$Sold=Daily dispatched cargo

TABULATE Sales ;Record daily dispatched cargo

TERMINATE 1 ;Daily timer

Figure 10. The structure of the Stock simulation program in GPSS-World system

The model consists of three main parts: the initial data declaration; simulation of cargo arrival process to warehouse; simulation of cargo dispatching process from the warehouse.

Four columns of the model include: labels; blocks and commands; operands of the blocks and commands; commentaries.

Additional information in the simulation model is marked with stars *, this information is ignored by the system translator.

The first block INITIAL declares parameters of transport batches, arriving to the warehouse. The next block INITIAL designates the “order point”, that shows moment of replenishment of the warehouse stock. The third block INITIAL designates the initial merchandise stock at the warehouse. The command TABLE (with label “Inventory”) forms a table for the changing stock. The second command TABLE is intended for offers for cargo to be delivered from the warehouse. The command VARIABLE interacts with generator of casual numbers, forms and gives them into the simulation model. The block GENERATE creates offers for dispatching cargo from the warehouse. The block TEST L testifies whether the stock occurs less than the insurance stock. The block ADVANCE moves the model time. The block SAVEVALUE forms new warehouse stock. The block TRANSFER transfers the model entry to the next block in accordance with the simulation algorithm.

The further blocks simulate delivery cargo from the warehouse.

The block GENERATE forms daily volume of dispatching cargo from the warehouse. The block ASSIGN forms demand for cargo. The block TABULATE writes in the TABLE with label «Inventory» data of stock. Block TEST GE testifies whether the stock in the warehouse is enough to make sure the order can be executed. The block SAVEVALUE decreases inventory at the warehouse by the volume of dispatched cargo in this day. The next block SAVEVALUE records the dispatched volume of cargo. The third block TABULATE puts in the TABLE with label “Sales” the volume of delivered cargo. The block TERMINATE counts number of fulfilled cycles and finishes simulation if the number occurs to be equal 0.

GPSS system shows results of simulation automatically in standard view, that is rather full (contains some dozens of values).

The results of simulation of warehouse stock with program GPSS-World include the data shown as an example in Figure 11:

GPSS World Simulation Report. GPSS – Stock. 2.25.2

TABLE MEAN STD.DEV. RANGE RETRY FREQUENCE CUM.%

INVENTORY 363,4 128, 6 0

- 300 24 24

300 350 35 59

350 400 17 76

400 450 17 93

450 500 0 93

500 550 1 94

550 - 6 100

SALES 81,2 6,4 0

- 70 3 3

70 80 43 46

80 90 44 90

90 100 10 100

SAVEVALUE RETRY VALUE

ACB 0 150

POINT 1 300

STOCK 1 234

SOLD 0 78

CEC XN PRI M1 ASSEM CURRENT NEXT PARAMETER VALUE

1 0 0,0 1 5 2

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

102 0 101 102 0 6

Figure 11. Form of the result table of the Stock simulation program

Simulation system GPSS World can display the results also as graphs with histograms of stock fluctuation (the table “Inventory”) and daily dispatching (table “Sales”).

The research with using of the simulation model is not revealed here. They can be easy executed by any expert depending on characteristics specific warehouse, parameters of material flows and other conditions.

7. Conclusion

In the article several methods of merchandise stock and storage areas of warehouses determination are represented. This information may be useful for projecting and research by the engineers who are interested and eager for reception more specific knowledge on the warehouses in supply chains, where warehouses are of great importance. These methods take into account probable fluctuation of warehouse stock during their operation in the logistic networks.

Literature

1. O. Malikov, Warehouses and Freight Terminals, Saint Petersburg, Russia, 2005,

660p.

2. O. Malikov. Business Logistics. Saint Petersburg, Russia, 2003, 223 p.

3. O.Malikov, Warehouses of Flexible Manufacturing Systems. Saint Petersburg,

Russia, 1986, 190 p.

4. O. Malikov, Automatic warehouses projecting. Saint Petersburg, Russia, 1981,

240 p.

5. O.Malikov. The Theory of Warehouse Systems. Network Logistics. Research

Report 211, 2009, p.15-24.

6. O.Malikov. Business Logistics: New Specific Approach to Concept. . Network

Logistics. Research Report 200, 2009, p.39-52.

7. V.Sergeev. Management at Business Logistics. – Moscow, 1997, 772p.

Contact information

Oleg B. Malikov

Doctor of Technical Sciences, professor, Member of Transport Academy of Russia.

Saint-Petersburg State Transport University of Transport, Department of Logistics & Freight

9, Moskovskey prospect, Saint Petersburg, 190031, Russia

E-mail: stadnitskey@mail.ru