Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Зинченко А.Б.

Южный федеральный университет. Россия

Инвестиционные игры с условиями дискретности

Партнерство и кооперация являются основными тенденциями современной экономики. Цель партнерства – максимизация общего дохода. Например, коллективное инвестирование позволяет создавать нестандартные вклады, увеличивающие выплаты [1]. Рассмотрим ситуацию с возможными инвестиционными проектами двух типов (допускающими произвольные неотрицательные вклады и вклады, кратными заданным числам) [2]. Обозначим: - множество проектов, - проекты с дискретными вкладами (, , ), - проекты с вкладами (). Вклад первого типа интерпретируется как инвестирование производственной технологии, пример вклада второго типа - банковский депозит. Пусть - множество инвесторов (игроков), , - капитал инвестора , , , , - процентные ставки, . Значения , , характеристической функции соответствующей кооперативной игры определяются задачами смешанного целочисленного программирования

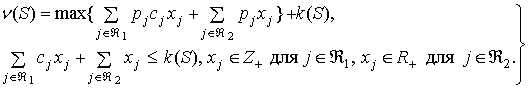(1)

Величина равна максимальной выплате, которую могут получить участники коалиции , объединяя капиталы и используя комбинации возможных вкладов. Нетрудно доказать, что задача (1) разрешима, ее единственное основное ограничение можно заменить равенством, а переменные , , где , можно исключить. Таким образом, (1) сводится к задаче

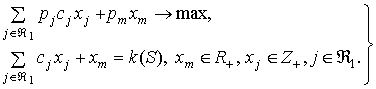
Если выполняется условие , соответствующее реальным инвестиционным проектам, и - оптимальное решение задачи

, (2)

то

, . (3)

Задача (2) – одна из простейших задач целочисленного линейного программирования, называемая задачей о ранце.

Игра относится к классу кооперативных игр с трансферабельной полезностью (ТП игр). Она монотонна и является частным случаем многопериодной инвестиционной игры, описанной в [2]. Анализ любой ТП игры , моделирующей практическую ситуацию, обычно начинается с проверки существования С-ядра

,

содержащего элементы множества дележей

,

удовлетворяющие условию коллективной рациональности. Игру с непустым С-ядром называют сбалансированной. В [2] было выведено следующее достаточное условие сбалансированности многопериодной инвестиционной игры

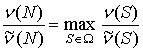, (4)

где - релаксированная игра, характеристическая функция которой определяется задачами линейного программирования, соответствующими задачам для . Покажем, что при однопериодном инвестировании функцию можно записать в явном виде. Положим . Из и , следует . Вектор , где

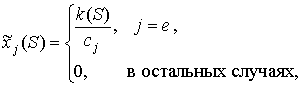(5)

является оптимальным решением релаксированной задачи (1) и

, . (6)

Из (4) и (6) получаем следующее достаточное условие сбалансированности однопериодной инвестиционной игры

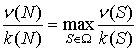. (7)

Пример 1. Рассмотрим проблему кооперативного инвестирования с четырьмя инвесторами и тремя инвестиционными проектами, первые два из которых – дискретные, т.е. , , , . Пусть: - вектор капиталов, - процентные ставки. Тогда , , , ,...,,..., и т.д. Используя формулы (2)-(3), проиллюстрируем процесс вычисления величины для коалиции в соответствующей инвестиционной игре :

, ,

.

Инвестиционная игра с характеристической функцией

, , , ,

, , ,

, ,

не выпукла (). Несмотря на то, что условие (7) не выполняется (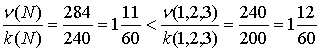), игра имеет непустое С-ядро .

Известно, что монотонной ТП игре соответствует единственная неотрицательная игра , удовлетворяющая условию , . называется 0-формой игры . В игре предполагается, что каждый агент уже получил ту часть величины , которую он мог бы иметь самостоятельно. Проблема распределения сводится к "справедливому" дележу остатка общего дохода. 0-нормализованная игра и ее решения более наглядны, чем исходные.

Для 0-формы инвестиционной игры рассмотрим достаточное условие сбалансированности, выведенное в [3]. Зафиксируем , , обозначим и положим

.

Если игра удовлетворяет условию

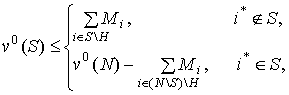(8)

для всех , то она имеет непустое С-ядро, содержащее вектор выигрышей , где

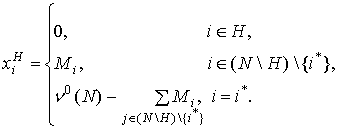
Численный эксперимент показал, что условие (8) выполняется для многих сбалансированных инвестиционных игр, не удовлетворяющих (7).

Пример 2. 0-форма инвестиционной игры четырех лиц, рассмотренной в примере 1, имеет вид: ,

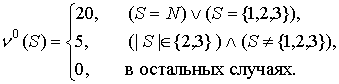
Игра сбалансирована, т.к. С-ядро инвариантно относительно 0-нормализации. Вычислим вклады игроков в максимальную коалицию: , . Возьмем , . Тогда , . Игра удовлетворяет достаточному условию сбалансированности (8). Вектор является крайней точкой ее С-ядра . Заметим, что значение Шепли игры не принадлежит ее С-ядру.

Литература:

1. Bonn P., Waegenaere A., Rafels C., Suijs J., Tijs S., Timmer J. Cooperation in capital deposits // OR Spektrum. 2001. V. 23. P. 265-281.

2. Waegenaere A.M.B., Suijs J.P.M., Tijs S.H. Stable profit sharing in cooperative investments // OR Spectrum. 2005. V. 27. №1. P 85-93.

3. Zinchenko A.B. A simple way to obtain the sufficient nonemptiness conditions for core of TU game // Contributions to game theory and management, St. Petersburg Graduate School of Management. 2013. V. 6. P. 447-457.