Экономические науки/8. Математические методы в экономике.

Д.ф.-м.н., профессор Юденков А.В.,

Сапкина Е.А.

ФГБОУ ВПО «Смоленская ГСХА», Россия

Изменение информации в сложных социальных системах в кризисных условиях

Моделирование процессов, протекающих в сложных социальных системах, является сложной задачей, требующей комплексного подхода.

Эффективным методом описания кризиса в сложной системе является использование основных положений термодинамики [1].

Рассмотрим процесс функционирования на рынке некоторой фирмы. Положим, что функционирование сводится к разрешению конфликтов, возникающих при взаимодействии с другими субъектами рынка и внешней средой. Тогда на макроуровне можно предложить следующую модель функционирования рынка [6].

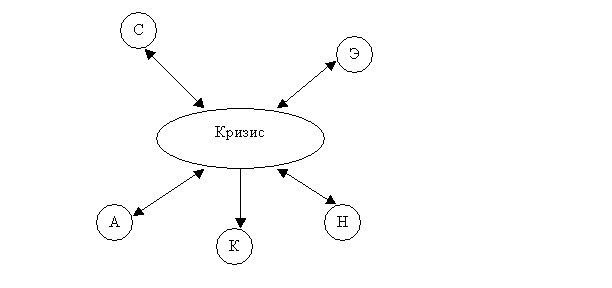
Рисунок 1

Здесь С – отношения содействия, Н – нейтралитет, А – соперничество, Э – эксплуатация. При функционировании конфликты переходят из одного макросостояния в другое.

Среди всех состояний сложной социальной системы особняком стоит конечное состояние – катастрофа (К). Попав в это состояние, система прекращает свое функционирование.

Основная идея термодинамического описания кризисов состоит в том, что при переходе из одного макросостояния в другое наблюдается максимум информации относительно управляющих параметров [1]. Поскольку информация в сложных социальных системах связана с энтропией, то эволюция в системе происходит согласно второму закону термодинамики. Однако при переходе системы в конечное состояние (катастрофы) информация о ней обнуляется, что может восприниматься как локальное нарушение общих термодинамических законов [5]. Предложим одну из возможных концепций по преодолению указанного противоречия. Заметим, что результаты носят качественный характер, но обладают достаточной общностью.

Введём следующие ограничения. Положим, что система имеет дискретное число базовых уровней, каждый из которых обладает определённой энергией. Система функционирует в евклидовом пространстве. Интервал времени будем считать комплексным, то есть состоящим из двух частей: реального времени – t и мнимого времени – τ.

Следуя подходу, изложенному в работе [4], для описания системы после катастрофы выберем чисто мнимый интервал времени ib = (t₂ – t₁) (Рисунок 2). Начальное состояние j₁ и конечное j₂ совпадают. Значит, b является периодом. Пусть состояние j₁, j₂, …, j_n образуют базис.

Запишем термодинамическую сумму Z при определенном внешнем фоне Т (в физических системах Т является температурой).

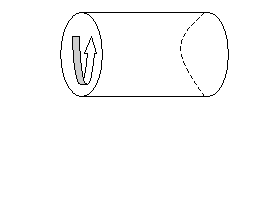
время t₂ – t₁ = ib

b j₁ = j₂

Рисунок 2

Иллюстрация эволюции системы за чисто мнимый промежуток времени [5].

Z = S exp (-b E_n) = exp (-kb²), (1)

где E_n – энергия системы на каждом базовом уровне, k – коэффициент (переменная), зависящий от топологии пространства [2].

Для того, чтобы получить среднее значение энергии системы продифференцируем ln Z по периоду b.

<E> = = 2bk (2)

Уравнение (2) устанавливает связь между энергией (размерами) системы, испытавшей катастрофу, и полным периодом мнимого времени, за которое система приходит в первоначальное состояние.

Воспользуемся следующим термодинамическим соотношением:

ln Z =

Здесь F – свободная энергия системы.

Так как

F = <E> - TS, то в состоянии катастрофы энтропия системы определяется формулой

S = 2bk. (3)

То есть, система и после катастрофы обладает определенной энтропией.

Рисунок 2 и формула (3) были получены в предположении, что функционирование системы происходит в пространстве Эвклида. При этом получается, что часть информации не пропадает, но выпадает из пространства.

Перейдем к пространству Минковского. В нем замкнутая линия информации Рисунка 2 перейдет в две ветви гиперболы (Рисунок 3).

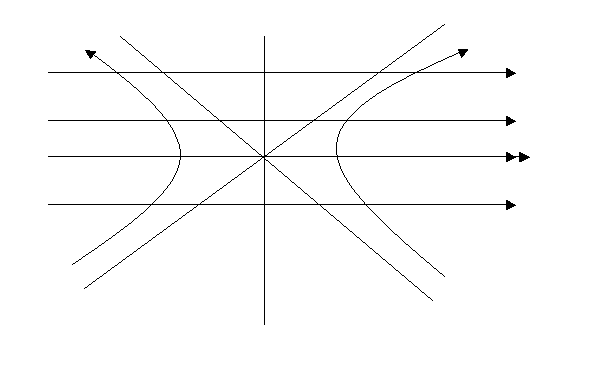S^- S⁺

Мировые линии

t=0

Рисунок 3.

Получается, что один оборот информации за мнимое время t=β рождает два кванта информации в реальном пространстве – времени Минковского. Один квант положительной информации идет в будущее, другой – отрицательный в прошлое, стирая память о системе, потерпевшей катастрофу. Таким образом, сложная система и после катастрофы генерирует информацию, обеспечивая справедливость второго закона термодинамики.

Литература:

1. Математическое моделирование кризисных ситуаций в сложной самоорганизующейся системе -Вестник БГТУ" №3(35), 2012. – с. 111 -113

2. Ландау Л.Д., Лившиц Е.М. Теория поля. -М. – ФИЗМАТЛИТ., 1986

3. Penrose R. Gravitational collaps and space-time singularities. Phys, Rev.lert, 14.57-9, 1965

4. Hawking S.W., Penrose R. The singularities of gravitational collaps and cosmology. Proc. Soc (London), А314, 529-41, 1970

5. С. Хокинг, Р. Пенроуз. Природа пространства и времени. -СПб. – Амфора. – 2013.

6. Новосельцев В.И. Теоретические основы системного анализа. – М.: Майор, 2006.