Синельник С.А.,

К.э.н. Коврижных О.Е.

Набережночелнинский институт Казанского (Приволжского) федерального университета, г. Набережные Челны, Россия

Определение меры сходства объектов

в кластерном анализе

«Кластерный анализ» – это общее название множества вычислительных процедур, используемых при создании классификации. В результате работы с процедурами образуются группы очень «похожих» объектов или «кластеры». Более точно, кластерный метод – это многомерная статистическая процедура, которая выполняет сбор данных, содержащих информацию о выборке объектов, а затем упорядочивает объекты в сравнительно однородные группы.

Примерами использования кластерного анализа являются следующие задачи: информатика – упрощение работы с информацией, визуализация данных, сегментация изображений, интеллектуальный поиск; экономика – анализ рынков и финансовых потоков, выведение закономерностей на фондовых биржах; маркетинг – сегментация рынков, анализ поведения потребителей, позиционирование товаров; астрономия – выделение групп звезд и галактик, автоматическая обработка космических снимков.

Для проведения кластерного анализа данных используют меры сходства [1]. Снит и Сокэл подразделили меры сходства на четыре вида: коэффициенты корреляции; меры расстояния; коэффициенты ассоциативности и вероятностные коэффициенты сходства. Хотя все четыре вида мер сходства широко применялись в свое время, лишь коэффициенты корреляции и расстояния получили широкое распространение [2].

1. Коэффициент корреляции – это показатель характера взаимного влияния изменения двух случайных величин. Он вычисляется по формуле:

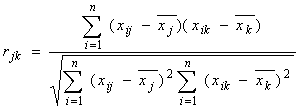, где – значение -й переменной для -го объекта; – среднее всех значений переменных -го объекта; – число переменных.

Значение коэффициента корреляции изменяется от -1 до +1, причем нуль указывает на то, что между объектами нет связи.

Главный недостаток коэффициента корреляции как меры сходства в том, что он чувствителен к форме за счет снижения чувствительности к величине различий между переменными. Кроме того, корреляция, вычисленная этим способом, не имеет статистического смысла.

Несмотря на эти недостатки, коэффициент широко использовался в приложениях кластерного анализа. Хаммер и Каннингхем показали, что при правильном применении кластерного метода коэффициент корреляции превосходит другие коэффициенты сходства, т.к. позволяет уменьшить число неверных классификаций [3].

2. Меры расстояния (метрики) пользуются широкой популярностью. Два объекта идентичны, если описывающие их переменные принимают одинаковые значения. В этом случае расстояние между ними равно нулю. Меры расстояния зависят от выбора шкалы (масштаба) измерений и обычно не ограничены сверху. Одним из наиболее известных расстояний является евклидово расстояние, определяемое как

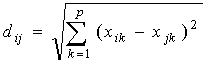, где – расстояние между объектами и ;

– значение -й переменной для -го объекта.

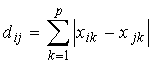Для придания больших весов более отдаленным друг от друга объектам используют квадрат евклидова расстояния.

Хорошо известной мерой также является манхеттенское расстояние, или «расстояние городских кварталов» (city-block).

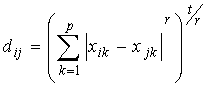Можно определить и другие метрики, но большинство из них являются частными формами специального класса метрических функций расстояния, известных как метрики Минковского.

Существуют расстояния, не являющиеся метриками Минковского, и наиболее важное из них – расстояние Махаланобиса . Формула метрики:

, где – общая внутригрупповая дисперсионно-ковариационная матрица, а и – векторы значений переменных для объектов и . В отличие от метрик Минковского и евклидовой, эта метрика связана с корреляциями переменных с помощью матрицы дисперсий-ковариаций.

Недостаток мер расстояния состоит в том, что оценка сходства сильно зависит от различий в сдвигах данных. Более того, метрические расстояния изменяются под воздействием преобразований шкалы измерения переменных.

3. Коэффициенты ассоциативности применяются, когда необходимо установить сходство между объектами, описываемыми бинарными переменными, причем 1 указывает на наличие переменной, а 0 – на ее отсутствие. Существуют три меры, которые широко используются: простой коэффициент совстречаемости, коэффициент Жаккара и коэффициент Гауэра.

4. Вероятностные коэффициенты сходства. Радикальное отличие этого типа от описанных выше заключается в том, что, сходство между двумя объектами не вычисляется. При образовании кластеров вычисляется информационный выигрыш от объединения двух объектов, а те объединения, которые дают минимальный выигрыш, рассматриваются как один объект. Вероятностные меры пригодны лишь для бинарных данных и прилагаются непосредственно к исходным данным до их обработки.

То, что некоторые вещи обнаруживают между собой сходство или различие, является весьма важным моментом для процесса классификации. Проблема сходства состоит не в простом распознавании сходных или несходных вещей, а в том, какое место эти понятия занимают в научных исследованиях.

Сегодня кластерный анализ является одним из наиболее эффективных инструментов обработки больших объемов данных и используется повсеместно, где применяется вычислительная техника.

Литература

1. Mark S. Aldenderfer, Roger K. Blashfield. Cluster Analysis. – SAGE Publications, Inc, 1984. – 88 p.

2. Сокэл Р.Р. Кластер-анализ и классификация: предпосылки и основные направления. В кн: Классификация и кластер // Под ред. Дж.Вэн Райзина М: Мир, 1980, с. 7-19

3. Hamer R., Cunningham J. Cluster analyzing profile data confounded with interrater differences: a comparison of profile association measures. – Applied Psychological Measurement, 1981, p. 63-72