Экономические науки/8. Математические методы в экономике
К.ф.-м.н. Зинченко А.Б., к.т.н. Мермельштейн Г.Г.,
Ефимова А.В.
Южный федеральный университет. Россия
Распределение прибыли при
партнерстве
страховых компаний
Конкуренция компаний на рынке страховых
услуг снижает их прибыль, в то время как партнерство позволяет страховать
риски, невыгодные для отдельных страховщиков. Модель ситуации распределения
премий и рисков между страховыми компаниями, использующая кооперативную ТП
игру, была впервые предложена в [1]. При некоторых условиях на входные
параметры, сбалансированность этой игры эквивалентна 1-выпуклости [2].
В докладе рассматривается содержательный
смысл неравенств из условия 1-выпуклости, их использование при описании других
прикладных кооперативных игр. Сравнивается 1-выпуклость и (классическая)
выпуклость, а также предлагается новое достаточное условие сбалансированности
игры страхования, обобщающее 1-выпуклость.
Ведем вначале необходимые обозначения и
понятия. Пусть 
- семейство функций 
, где 
, 
, 
. При фиксированном 
функцию 
отождествляют с
кооперативной ТП игрой 
. Маргинальным вкладом называют вклад игрока в
максимальную коалицию
, 
. (1)
Игра 
: неотрицательна, если 
, 
; монотонна, если 
, 
; (0-1)-нормализована, если
, 
, 
; (2)
сбалансирована,
если имеет непустое С-ядро
;
выпукла,
если 
для 
; вогнута, если
, 
;
(3)
1-выпукла,
если
, 
, 
. (4)
Характеризующим свойством 1-выпуклой игры является
совпадение ее С-ядра с множеством двойственных дележей
.
Любая выпуклая или 1-выпуклая игра 
сбалансирована.
Кооперативная игра страхования 
, где 
- множество страховых
компаний, 
,
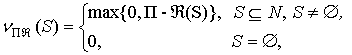
однозначно определяется страховой премией 
и невозрастающей
функцией 
(
, 
), где 
соответствует оптимальному
распределению данного риска 
между компаниями
коалиции 
, 
,
, 
- вещественный
неотрицательный функционал, 
для всех 
. Методы вычисления 
и 
описаны в [2]. Семейство
всех игр страхования (insurance games) с 
страховщиками
обозначим через 
. Игра 
компромиссно
устойчива [3]. Она обобщает известную кооперативную игру банкротства [4]. Одним
из основных свойств игр страхования является совпадение 
с множеством всех
монотонных неотрицательных игр 
.
В работе [2] доказано, что при выполнении
условия 
, где
, 
,
сбалансированность игры страхования с премией 
эквивалентна ее
1-выпуклости. Если 
, то 1-выпуклость является только достаточным, но не
необходимым условием непустоты С-ядра игры 
.
Первая часть условия 1-выпуклости (4)
обеспечивает непустоту множества 
. Прибыль 
, которую могут получить страховщики при полном объединении,
не должна быть больше суммы их маргинальных вкладов 
. Вторая часть условия (4)
требует, чтобы сумма маргинальных вкладов 
любой подгруппы игроков 
(
) быта не больше вклада 
этой подгруппы в
максимальную коалицию 
. Содержательно вторая часть условия (4), называемая условием
союза, означает, что страховщики успешней действуют в объединении, чем
самостоятельно. Условие союза используется также при описании класса клановых
игр, содержащего подкласс игр большого босса.
Подставив (1) в условие союза, получаем
систему
, 
.
(5)
Для 
-элементной коалиции 
неравенство из (5)
имеет вид
,
т.е. содержится в (3). Таким образом, часть неравенств
условия 1-выпуклости являются неравенствами вогнутости.
Поскольку С-ядро любой ТП игры инвариантно
относительно (0-1)-нормализации, при анализе сбалансированности игры достаточно
рассматривать ее (0-1)-форму. При (0-1)-нормализации конус 
трансформируется в
политоп (polytope) 
. Обозначим через 
и 
подмножества выпуклых
(convex) и 1-выпуклых (1-convex) игр, принадлежащих 
. Представляет интерес соотношение между политопами 
и 
, а также определяющие их неприводимые системы. Минимальный
тест [5] на выпуклость игры 
состоит из 
неравенств
, 
,
,
. (6)
Если 
, то (6) становится условием неотрицательности.
Следовательно, для игры 
необходимо проверять
выполнение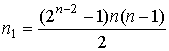 
неравенств. Система
(4) состоит из 
неравенств, но для 
и 
-элементных коалиций 
, 
, они становятся тождествами. Таким образом, 1-выпуклость
игры 
определяется 
неравенствами.
Значения 
и 
для игр с малым 
приведены в таблице
1.
Таблица 1
Количество неравенств в системах, определяющих 
и 
|
Число
игроков |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
3 |
18 |
70 |
225 |
651 |
1764 |
4572 |
|
|
4 |
11 |
26 |
57 |
120 |
247 |
502 |
)
)
Пример 1. Рассмотрим неотрицательную (0-1)-нормализованную
игру 
трех лиц, 
. Условие 1-выпуклости состоит из 4 неравенств
, 
, 
, 
,
первые
три из которых – неравенства вогнутости. Минимальный тест на выпуклость имеет
вид
, 
, 
.
Вычислив вершины политопов 
и 
, получаем
, 
.
Значения 
, 
, для одноэлементных и максимальной коалиций определены (2),
остальные - даны в таблице 2. Заметим, что вершины 
, 
, политопа 
являются играми
большого босса с игроком 
в качестве босса, а
вершины 
, 
политопа 
- играми единогласия
двухэлементных и трехэлементной коалиций. Из 
и выпуклости
политопов получаем 
.
Пример 2. Для игр четырех лиц 
, 
. Целочисленные вершины политопа 
, как и в примере 1, являются играми большого босса, а целочисленные
вершины 
- играми единогласия.
Множества 
и 
имеют единственный
общий элемент – симметричную игру 
, где 
, 
для двухэлементных
коалиций, 
- для трехэлементных,
а остальные значения определены условием (2).
Таблица 2
Координаты вершин политопов 
и 
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1/2 |
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1/2 |
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1/2 |
0 |
0 |
1 |
0 |
Обобщением примеров 1 и 2 является
теорема, утверждающая, что единственная игра из 
может быть
одновременно выпуклой и 1-выпуклой.
Теорема 1. 
, где
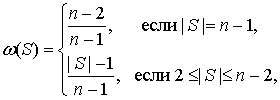
остальные значения 
определены
аналогично (2).
Доказательство использует утверждение [2]:
выпуклая игра 
является 1-выпуклой
тогда и только тогда, когда 
, 
.
В следующей теореме формулируется новое
достаточное условие сбалансированности игры страхования, обобщающее условие
1-выпуклости.
Теорема 2. Если 
и для всех 
выполняется условие
, 
, (7)
где 
и 
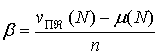, то 
.
Доказательство
основано на результатах из [6].
Геометрически условие (7) означает, что
центр 
множества двойственных
дележей игры страхования (
, 
) принадлежит ее С-ядру 
, в то время как условие 1-выпуклости означает совпадение
множеств 
и 
. Следовательно, подмножество сбалансированных игр из 
, удовлетворяющее (7), содержит конус 1-выпуклых игр
страхования, но не совпадает с ним. Количество неравенств в (7) равно 
.
Пример 3. Рассмотрим игру с тремя страховщиками, 
, страховой премией 
и функцией 
, где
, 
, 
, 
, 
.
В данном случае 
, т.к.
, 
,
Соответствующая игра страхования 
,
, 
, 
, 
, 
,
не выпукла, т.к. 
, и не 1-выпукла, т.к.
, 
,
.
Тем не менее, игра сбалансирована. Ее С-ядро не
совпадает с множеством двойственных дележей
,
где 
, 
, 
, 
, 
. Покажем, что игра удовлетворяет условию Теоремы 2. Вычислив
, 
, 
,
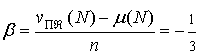получаем
, 
, 
,
, 
,
, 
.
В качестве исхода данной игры можно рекомендовать
"центр тяжести" С-ядра (среднее арифметическое вершин), согласно
которому прибыль первой, второй и третьей страховой компании соответственно
равна 
, 
и 
(д.е.) или вектор
Шепли 
.
Литература:
1. Fragnelli V.,
Marina M.E. Co-insurance games and environmental pollution risk. In: Game
Practice and the Environment. Edward Elgar Publishing, Cheltenham (UK), 2004,
pp. 145–163.
2. Driessen T.S.H., Fragnelli V., Katsev I.V., Khmelnitskaya A.B. A game theoretic approach to
co-insurance situations // Contributions to Game Theory and Management. 2010. V.3.
P. 49–66.
3. Quant M., Borm P.,
Reijnierse H., van Velzen B. The core cover in relation to the nucleolus and
the Weber set // International Journal of Game Theory. 2005. V. 33. P. 491–503.
4. Aumann R.J.,
Maschler M. Game theoretic analysis of a bankruptcy problem from the Talmud //
Journal of Economic Theory. 1985. V. 36. P. 195–213.
5. Voorneveld, M.,
Grahn S. A minimal test for convex games and the Shapley value. Working paper
series. Department of economics. Uppsala university. 2001. № 2. P. 1–8.
6. Zinchenko A.B. A
simple way to obtain the sufficient nonemptiness conditions for core of TU game
// Contributions to game theory and management. 2013. V. 6. P. 447-457.