Современные информационные
технологии/ 2. Вычислительная техника и программирование
Илипов М.М., к.ф.-м.н. Искакова А.С.
Евразийский национальный университет им. Л.Н.
Гумилева, Казахстан
Механизм вывода прецедента по введенному ситуационному
вектору в системе Matlab
Одними
из характерных особенностей поставленных перед совершенствованием работы RFID являются составление и
изучение алгоритма выбора прецедента при наблюдении ситуационного вектора с
количественными координатами.
Ранее
в работе Прохорова М. Д. и Федунова Б.Е. [1] был введен алгоритм выбора прецедента при наблюдении
ситуационного вектора с количественными координатами.
Аналогично
результатам работы [1] представим матрицу знаний по прецедентам.
Пусть
состояние ПрС/С описывается ситуационным вектором с координатами (х1, …, xn) и каждая координата хi - лингвистическая переменная с множеством
термов прецедентам (блок прецедента). Каждая строка матрицы представляет собой
конкретный ситуационный вектор, при котором в прошлом успешно реализовался соответствующий
прецедент.
Таблица
1
№
п/п |
Координаты
ситуационного вектора
|
Прецедент
|
|||
|
x1 |
x2 |
… |
x n |
||
|
|
|
|
|
|
d1 |
|
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
dj |
|
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
dm |
Перенумеруем строки блока прецедента dj двумя индексами: первый
индекс – номер прецедента (здесь он является номером блока), второй индекс –
порядковый номер ситуационного вектора в этом блоке.
Введённая матрица определяет систему логических
высказываний вида «если …, то …, иначе …». Например,
строка матрицы j1 шифрует высказывание:
Если 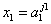 и
и 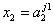 и … и
и … и
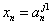 , то dj
, (1)
, то dj
, (1)
иначе аналогичное
выражение для следующей строки и т. д.
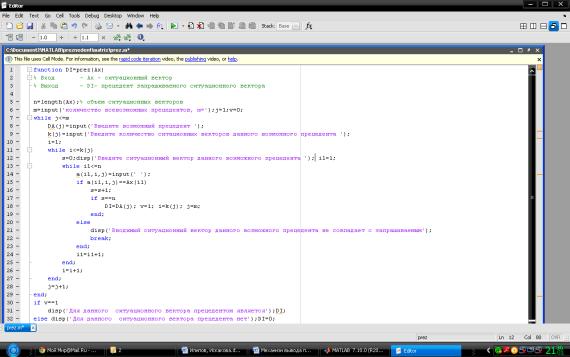
Рис. 1. Алгоритмизированная программа в системе Matlab для вывода
прецедента по введеному ситуационному вектору
Полученную упорядоченную таким образом систему
логических высказываний называют нечёткой матрицей знаний или просто – матрицей
знаний.
Алгоритмизированная программа в системе Matlab для вывода
прецедента по введеному ситуационному вектору представлена представлена
на рисунке 1.
Рассмотрим в качестве примера поведение
кода NRZ антиколлизионного алгоритма двоичного поиска, представленные в работе
[2, стр. 164].
Пусть поведение кода NRZ описывается
ситуационным вектором с координатами{x1, x2,…, xn},
представленными лингвистическими переменными:
x1 – уровень сигнала, поднесущей из транстпортера
№1;
x2 - уровень сигнала,
поднесущей из транстпортера №2;
и так далее;
xn - уровень сигнала, поднесущей из
транстпортера № n.
Пусть для этого класса наблюдались два
прецедента d1, d2, каждый из которых
применялся в двух (разных) случаях. Так согласно работе [2], если хотя бы один
из n транспортеров посылает
сигнал высокого уровня, тогда получаем прецедент d1, высокого уровня.
Лингвистические переменные принимают следующие
унифицированные значения (термы): xi
= {статический низкий уровень, статический высокий уровень }, i = 1, …, n.
Матрица знаний для этой системы представлена
в табл.2.
Таблица 2.
|
№ п/п |
Координаты ситуационного вектора
|
Прецеденты |
|||
|
x1 |
x2 |
… |
xn |
||
|
1.1 1.2 1.3 … |
выс. выс. низк. … |
выс. низк. выс. … |
… … |
выс. низк. низк. … |
d1 |
|
2.1 |
низк |
низк. |
… |
низк. |
d2 |
Анализ проведенных в настоящей работе
исследований позволяет сформулировать следующие основные результаты.
а) предложены
и изучены матрицы по прецедентам с приведением примера, описывающего поведение кода NRZ антиколлизионного
алгоритма двоичного поиска;
б) построена
алгоритмизированная программа для вывода прецедента по введенному ситуационному
вектору.
Литература:
1. Прохоров М. Д. Федунов
Б.Е. Вывод по прецеденту в базах знаний бортовых интеллектуальных систем,
размещаемых на борту антропоцентрических объектов.
2. Дшхунян В.Л.
Электронная идентификация. Бесконтактные электронные идентификаторы и
смарт-карты / В.Л. Дшхунян, В.Ф. Шаньгин. – М.: ООО «Издательство АСТ»:
Издательство «НТ Пресс», 2004. – 695 с.