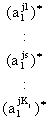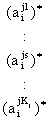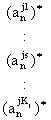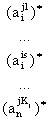Современные информационные
технологии/ 2. Вычислительная техника и программирование
Илипов М.М., к.ф.-м.н. Искакова А.С.
Евразийский национальный университет им. Л.Н.
Гумилева, Казахстан
Алгоритм вычисления Минимакс для
определения предпочтения прецедентов в системе Matlab
Одними
из характерных особенностей поставленных перед совершенствованием работы RFID являются составление и
изучение алгоритма выбора прецедента при наблюдении ситуационного вектора с
количественными координатами.
Ранее
в работе Прохорова М. Д. и Федунова Б.Е. [1] был введен алгоритм выбора прецедента при наблюдении
ситуационного вектора с количественными координатами.
Аналогично
результатам работы [1] представим матрицу знаний по прецедентам.
Пусть
состояние ПрС/С описывается ситуационным вектором с координатами (х1, …, xn) и каждая координата хi - лингвистическая переменная с множеством
термов прецедентам (блок прецедента). Каждая строка матрицы представляет собой
конкретный ситуационный вектор, при котором в прошлом успешно реализовался
соответствующий прецедент.
Таблица
1
№
п/п |
Координаты
ситуационного вектора
|
Прецедент
|
|||
|
x1 |
x2 |
… |
x n |
||
|
|
|
|
|
|
d1 |
|
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
dm |
Перенумеруем строки блока прецедента dj двумя индексами: первый
индекс – номер прецедента (здесь он является номером блока), второй индекс –
порядковый номер ситуационного вектора в этом блоке.
Введённая матрица определяет систему логических
высказываний вида «если …, то …, иначе …». Например,
строка матрицы j1 шифрует высказывание:
Если 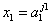 и
и 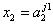 и … и
и … и
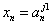 , то dj , (1)
, то dj , (1)
иначе аналогичное
выражение для следующей строки и т. д.
Представим алгоритм определения функции принадлежности
прецедента dj можно записать в виде:
а) фиксируем
произвольную точку (![]() ,
,
б) для каждого
блока матрицы знаний, соответствующего dj, определяем mdj (x1, .. xi, .. xn)
в этой точке согласно схеме таблицы 2.
Таблица 2.
|
№ п/п |
Координаты
ситуационного вектора
|
max |
min |
d |
||||
|
x1 |
|
xi |
|
xn |
||||
|
: |
: |
: |
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
|
|
|
|
Заметим, что
для фиксированной точки ![]() блок матрицы,
представленный в таблице 3, является числовым, так как вместо каждого терма
блок матрицы,
представленный в таблице 3, является числовым, так как вместо каждого терма ![]() из этого блока поставлено значение его
функции принадлежности
из этого блока поставлено значение его
функции принадлежности ![]() ,
вычисленное в соответствующей
,
вычисленное в соответствующей ![]() . Операция
. Операция ![]() производится над
числами, стоящими в строках “i”,
1≤i≤n и в столбец “min” заносится минимальное
число в соответствующей строке. Операция
производится над
числами, стоящими в строках “i”,
1≤i≤n и в столбец “min” заносится минимальное
число в соответствующей строке. Операция
![]()
![]()
![]()
![]() выделяет среди полученных строчных минимумов
1 £ js £Kj наибольший. Это число и
является значением функции принадлежности mdj (x1, .. xi, .. xn)
в этой фиксированной точке
выделяет среди полученных строчных минимумов
1 £ js £Kj наибольший. Это число и
является значением функции принадлежности mdj (x1, .. xi, .. xn)
в этой фиксированной точке ![]() .
Проведя такие вычисления для каждой точки универсального множества, получим
интересующие нас функции принадлежности.
.
Проведя такие вычисления для каждой точки универсального множества, получим
интересующие нас функции принадлежности.
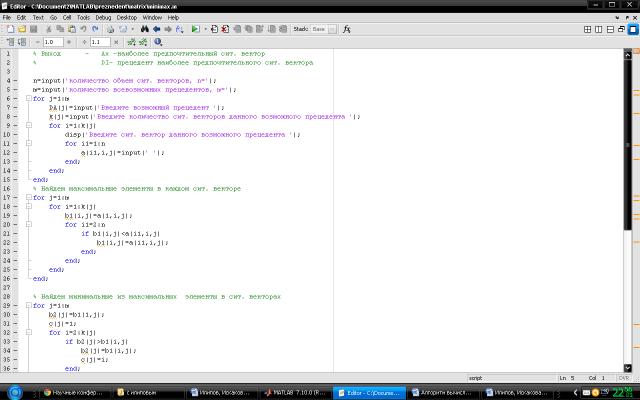
Рис. 1. Алгоритмизированная программа в системе Matlab для выбора прецедента по методу Максимин при
наблюдении ситуационного вектора с количественными координатами
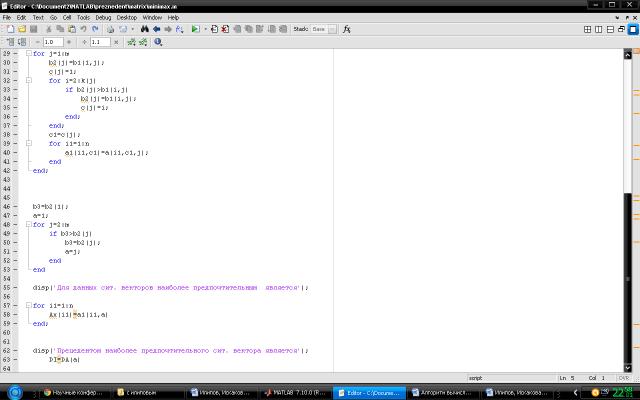
Рис. 2. Продолжение алгоритмизированной программы
в системе Matlab для выбора
прецедента по методу Максимин при наблюдении ситуационного вектора с
количественными координатами
Полученную упорядоченную таким образом систему
логических высказываний называют нечёткой матрицей знаний или просто – матрицей
знаний.
Алгоритмизированная программа в системе Matlab для
выбора прецедента по методу Максимин при наблюдении ситуационного вектора с
количественными координатами представлена на рисунках 1-2.
Литература:
1. Прохоров М. Д. Федунов
Б.Е. Вывод по прецеденту в базах знаний бортовых интеллектуальных систем,
размещаемых на борту антропоцентрических объектов.
2. Дшхунян В.Л.
Электронная идентификация. Бесконтактные электронные идентификаторы и
смарт-карты / В.Л. Дшхунян, В.Ф. Шаньгин. – М.: ООО «Издательство АСТ»:
Издательство «НТ Пресс», 2004. – 695 с.