Жолдыбаев М.Е.
Актюбинский региональный государственный
университет им. К.Жубанова, Казахстан.
Оценка решений краевой задачи с начальным скачком для сингулярно
возмущенных дифференциальных уравнений в частных производных второго порядка
1.
Постановка задачи.
Рассмотрим в
области ![]() линейное сингулярно
возмущенное дифференциальное уравнение вида:
линейное сингулярно
возмущенное дифференциальное уравнение вида:
![]() (1)
(1)
удовлетворяющее краевым
условиям:
![]() ,
, ![]() . (2)
. (2)
Здесь ![]() - малый параметр,
- малый параметр, ![]() - независимые переменные,
- независимые переменные, ![]() - искомая функция,
- искомая функция, ![]() ,
,![]() и
и ![]() функции заданные в
области
функции заданные в
области ![]() , а операторы:
, а операторы: ![]() , где функция
, где функция ![]() также задана в
области
также задана в
области ![]() .
.
Предположим, что:
1) функции ![]() ,
,![]()
![]() и
и ![]() - достаточно гладкие
по совокупности аргументов
- достаточно гладкие
по совокупности аргументов ![]() :
:
2) ![]() ,
, ![]() ,
, ![]() ,
,
где ![]() ,
, ![]() - некоторые вещественные числа;
- некоторые вещественные числа;
3) функции ![]() и
и ![]() являются решениями
уравнения характеристики:
являются решениями
уравнения характеристики:
![]()
соответствующего уравнению
(1), и удовлетворяющее начальным условиям
![]()
Цель работы:
установить оценки решения ![]() сингулярно [1] возмущенной краевой задачи с начальным
скачком (1), (2);
сингулярно [1] возмущенной краевой задачи с начальным
скачком (1), (2);
2. Оценка
решения. В
данном параграфе доказана следующая
Теорема. Если выполнены
условия 1)- 2), то для
решения ![]() сингулярно
возмущенной краевой задачи (1), (2) в
области
сингулярно
возмущенной краевой задачи (1), (2) в
области ![]() (вдоль каждой
характеристики
(вдоль каждой
характеристики ![]() для любого
для любого ![]() ) справедливы следующие оценки:
) справедливы следующие оценки:
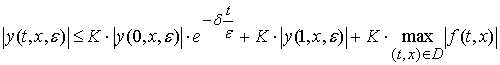 , (3)
, (3)
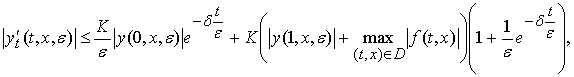
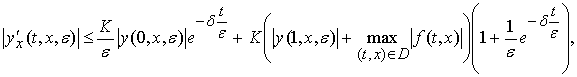
где ![]() и
и ![]() - некоторые
постоянные, не зависящие от
- некоторые
постоянные, не зависящие от ![]() и
и ![]() .
.
Доказательство. Действительно, непосредственной проверкой можно
убедиться, что решение сингулярно
возмущенной краевой задачи (1) и (2) представимо в виде:
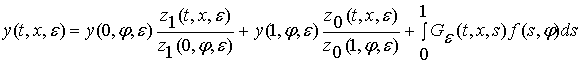 , (4)
, (4)
где функции ![]() и
и ![]() .
.
Способом аналогичным, как в
[2] для 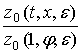 и
и 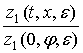 получим в области
получим в области ![]() (вдоль каждой
характеристики
(вдоль каждой
характеристики ![]() для любого
для любого ![]() ) следующие
представления:
) следующие
представления:
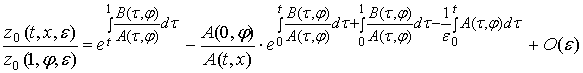 ,
,
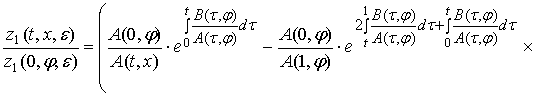
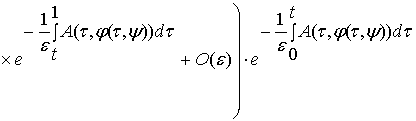 ,
(5)
,
(5)
где функции ![]() и
и ![]() те же, что и в [3].
те же, что и в [3].
Откуда, учитывая что функции
![]() , получаем следующие оценки:
, получаем следующие оценки:
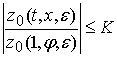 ,
, 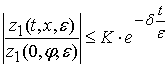 .
(6)
.
(6)
Из (4), вспоминая оценки (6) и функции типа Грина [2] а также
непрерывность функции ![]() , получим оценки для решения
, получим оценки для решения ![]() в (3). Из
формулы (4) найдем:
в (3). Из
формулы (4) найдем:
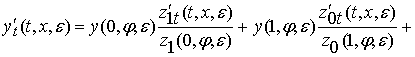
 .
.
Для функций 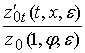 и
и 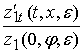 на основание
формулы (5) в области
на основание
формулы (5) в области ![]() (вдоль каждой
характеристики
(вдоль каждой
характеристики ![]() для любого
для любого ![]() ) справедливы
следующие представления:
) справедливы
следующие представления:
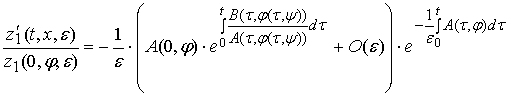 ,
,
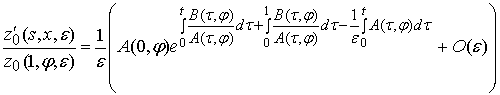 .
.
Из последних соотношений с
учетом условия 1)-2) получаем следующие
оценки:
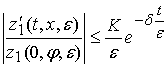 ,
, 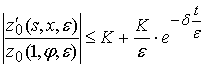 .
.
Следовательно, учитывая
оценки функция типа Грина [2], получим оценки (3) в области ![]() (вдоль каждой
характеристики
(вдоль каждой
характеристики ![]() для любого
для любого ![]() ) для частных
производных
) для частных
производных ![]() , Теперь вспомнив, что
, Теперь вспомнив, что ![]() есть скалярное произведение векторов
есть скалярное произведение векторов ![]() и
и 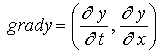 , получим
, получим
![]() , (7)
, (7)
где ![]() ,
, 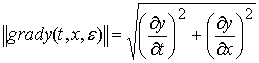 ,
, ![]() .
.
Из (4), учитывая
(7), получим оценки (3) в области ![]() (вдоль каждой
характеристики
(вдоль каждой
характеристики ![]() для любого
для любого ![]() ) для частных производных
) для частных производных ![]() . Теорема доказана.
. Теорема доказана.
Литература
1. Ломов С.А. Введение в общую теорию сингулярных возмущений. М.Наука,
1981, 400 с.
2. Касымов К.А. Линейные
сингулярно возмущенные дифференциальные уравнения второго порядка. Алма-Ата:
Наука, 1981. 123 с.
3. Тажимуратов И.Т., Жолдыбаев М.Е., Оценки
решений сингулярно-возмущенных уравнений в частных производных второго порядка. // Известия НАН РК. 2000, № 3, с. 56-62.