Математика/1.Дифференциальные и интегральные уравнения

Даулетбаева Ж.Д., старший преподаватель

Костанайский государственный университет, Казахстан

Преобразования Лапласа

Пьер-Симо́н, маркиз де Лапла́с (фр. Pierre-Simon de Laplace; 23 марта 1749 — 5 марта 1827) — французский математик, механик, физик и астроном.

Фундаментальными являются его работы по дифференциальным уравнениям, в частности первые общие методы интегрирования уравнений в частных производных (метод каскадов), а также метод производящих функций и так называемое преобразование Лапласа, с особенным успехом применяемое в математике.

Многочисленные задачи электротехники, гидродинамики, механики, теплопроводности, математической физики, радиотехники эффективно решаются преобразование Лапласа

Преобразование Лапласа — интегральное преобразование, связывающее функцию F(s)комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Применение этого метода позволяет решать дифференциальные уравнения, уравнения в частных производных, а также интегро-дифференциальные уравнения типа свёртки.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями [1].

Функцией-оригиналом мы будем называть любую комплексную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

1) Функция f(t) удовлетворяет условию Гёльдера всюду на оси t , кроме отдельных точек, где она имеет разрывы первого рода, причем на каждом конечном интервале таких точек конечное число. Это означает, что для каждого t (кроме указанных исключительных точек) существуют положительные постоянные А, и h такие, что

2) f(t)= 0 для всех отрицательных t.

3) f(t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М > 0, s₀ > 0, что для всех t

Число s₀ назовем показателем роста f(t); для ограниченных оригиналов можно, очевидно, принять s₀ = 0.

С точки зрения физических приложений условия 1) и 3) не нуждаются в пояснениях — они, очевидно, выполняются для большинства функций f(t), описывающих физические процессы (t интерпретируется как время). Условие 2) на первый взгляд кажется искусственным. Однако следует иметь в виду, что операционный метод приспособлен к задачам, приводящим к решению дифференциальных уравнений с данными начальными условиями. В таких задачах вся информация о ходе процесса до момента начала наблюдения, за который, конечно, можно принять момент t = 0, содержится в начальных условиях. Таким образом, и условие 2) физически вполне естественно.

Изображением функции f(t) (по Лапласу) называют функцию комплексного переменного , определяемую соотношением

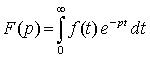
где интеграл берется по положительной полуоси. Фразу: «функция f(t) имеет своим изображением F(p)» мы будем записывать символами:

,

.

Смысл этого обозначения: оригиналу f сопоставлено изображение F, а изображение F имеет своим оригиналом f [2].

Пользуясь определением, найти изображение функции

Решение. Для функции имеем . Поэтому изображение будет определено и аналитическое Re p>0 в полуплоскости. Применяя к этой функции преобразование Лапласа получим

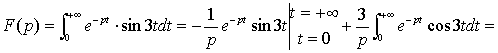
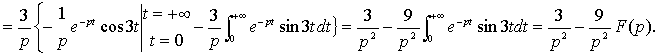
Получили равенство:

Оттуда находим

Таким образом, справедливо следующее соответствие:

Итак, применение методов, использующих преобразование Лапласа нашло широкое применение в решении различных задач электротехники, гидродинамики, механики, теплопроводности, радиотехники.

Литература:

1 Труфанова Т.В. Интегральное преобразование Лапласа и Фурье: Учебное пособие / Т.В. Труфанова, Е.М. Салмашова. - Благовещенск: Амурский гос. ун-т, 2006.

2 Владимиров В.С. Уравнение математической физики – Москва «Наука», 1981.