Математика/1.Дифференциальные и интегральные уравнения

Д.ф.-м.н. Городецький В. В.

Чернівецький національний університет імені Юрія Федьковича,Україна

Нелокальна за часом задача для еволюційних рівнянь з операторами Бесселя нескінченного порядку

Предметом досліджень багатьох вітчизняних та зарубіжних математиків є еволюційні рівняння з псевдодиференціальними операторами, побудованими за допомогою певних інтегральних перетворень за певними функціями (символами). До таких операторів відносяться і оператори вигляду , породжені перетвореннями Бесселя та . Якщо символ є цілою функцією аргументу , то рівняння із вказаним оператором містять сингулярні диференціальні рівняння (тобто рівняння, серед коефіцієнтів яких є такі, що необмежені в деякій області), зокрема, рівняння з оператором Бесселя , , який має у своїй структурі вираз і формально зображається у вигляді . Якщо , де – поліном змінної при фіксованих , , що задовольняє певну умову «параболічності», то таке рівняння відноситься до -параболічних рівнянь, введених М. І. Матійчуком та В. В. Крехівським в [1]. Такі рівняння вироджуються на межі області й за внутрішніми властивостями вони близькі до рівномірно параболічних рівнянь.

Еволюційні рівняння з оператором

, ,

який надалі називатимемо оператором Бесселя нескінченного порядку, досліджували О. В. Мартинюк, С. С. Дрінь та В. В. Городецький [2-4]. З’ясовано, що такий оператор можна розуміти як псевдодиференціальний оператор вигляду , якщо функція-символ є цілою функцією за змінною . Встановлено коректну розв’язність задачі Коші для еволюційного рівняння з оператором у випадку, коли початкова функція є аналітичним функціоналом із простору типу . На теперішній час актуальним є дослідження нелокальних багатоточкових задач для еволюційних рівнянь з операторами Бесселя нескінченного порядку з граничними умовами у тих чи інших функціональних просторах, зокрема, у просторах узагальнених функцій (встановлення їх коректної розв’язності, побудова та властивості розв’язків тощо).

Нелокальні задачі виникають при описі всіх коректних задач для конкретного оператора, при побудові загальної теорії крайових задач. Крім того, багато прикладних задач моделюються крайовими задачами для рівнянь з частинними похідними з нелокальними умовами (теорія фізики плазми, ядерних реакцій, вологопереносу, коливання різних систем, поширення електромагнітних хвиль, демографічні дослідження, тощо).

Розглянемо еволюційне рівняння

, , (1)

де – оператор Бесселя нескінченного порядку, побудований за символом , який, як функція , допускає аналітичне продовження у всю комплексну площину. Для рівняння (1) поставимо задачу: знайти розв’язок цього рівняння, який задовольняє умову:

(2)

( – простір Л. Шварца швидко спадних на нескінченності функцій), , , – фіксовані числа, при цьому вважаємо, що , . Класичний розв’язок задачі (1), (2) шукаємо за допомогою перетворення Бесселя. У результаті отримаємо, що розв’язок такої задачі, яку надалі називатимемо нелокальною багатоточковою за часом задачею для рівняння (1), зображається формулою

,

де – оператор узагальненого зсуву аргументу, що відповідає оператору Бесселя [5],

, .

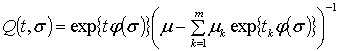При фіксованому функція є елементом простору ; , , як абстрактна функція параметра із значеннями в просторі , диференційовна по , і в просторі – просторі, топологічно спряженому до , справджується граничне співвідношення

(тут – дельта-функція Дірака). Правильним є наступне твердження.

Лема. Нехай . Тоді в просторі справджується граничне співвідношення

.

З леми випливає, що для рівняння (1) багатоточкову за часом задачу можна ставити так: знайти розв’язок рівняння (1), який задовольняє умову

, (3)

де , , (границі розглядаються у просторі ).

Теорема. Задача (1), (3) є коректно розв’язною; розв’язок подається у вигляді згортки

,

при цьому , .

Література:

1. Крехивский В. В. Фундаментальные решение и задача Коши для линейных параболических систем с оператором Бесселя / В. В. Крехивский, М. И. Матийчук // Докл. АН СССР. – 1968. – Т.181, №6. – С. 1320-1323.

2. Городецький В. В. Оператори Бесселя нескінченного порядку та їх застосування / В. В. Городецький, О. В. Мартинюк // Доп. НАН України. – 2003. – №6. – С. 7-12.

3. Мартинюк О. В. Задача Коші для еволюційних рівнянь з оператором Бесселя нескінченного порядку / О. В. Мартинюк // Науковий вісник Чернівецького університету: зб. наук. праць. Вип. 134. Математика. – Чернівці: Рута, 2002. – С. 71-83.

4. Городецький В. В. Задача Коші для еволюційних сингулярних рівнянь нескінченного порядку / В. В. Городецький, С. С. Дрінь // Доп. НАН України. – 2003. – №11. – С. 12-17.

5. Левитан Б. И. Разложение по функциям Бесселя в ряды и интегралы Фурье / Б. И. Левитан // Успехи мат. наук. – 1951. – Т.6, Вып. 2. – С. 102-143.