Математика/5. Математическое моделирование

      к.ф.-м.н. доц. В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия,

                          кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

МАТРИЧНОЕ МОДЕЛИРОВАНИЕ УНАРНЫХ ОПЕРАЦИЙ

 

         § 1. Структура простого суждения

 

         В логике суждение является самой основной, первичной логической формой. Это простое предложение имеет свою типичную структуру, состоящую из четырёх основных частей.

         Первая часть суждения отражает количественную характеристику рассматриваемых объектов и является служебным словом. Эта часть называется квантором и обозначатся символом «k». В классической логике используется два вида кванторов:

         квантор всеобщности, который обозначается символом  и читается «все…», «для всех…», «абсолютно все…»;

         квантор существования, который обозначается символом  и читается «часть…», «некоторые…», «существуют…», «не все…».

         Второй частью высказывания является главный термин, который называется субъектом и обозначается S,  он   играет роль подлежащего и определяет то, о чём говорится в предложении.

         Третьей частью высказывания является служебное слово, которое устанавливает взаимосвязь между предметом мысли и его утверждаемым свойством. Этот служебное слово называется связкой или мостиком и обозначается символом  m. Мостик отражает качественную характеристику высказывания.     Различаются два вида мостиков:

негативный мостик, который характеризует отрицание предполагаемого свойства, и обозначается символом « –/–  »,

позитивный мостик, который характеризует утверждение предполагаемого свойства, и обозначается символом    « —  ».

         Последней  частью суждения является свойство, которое утверждается или отвергается в данном предложении. Этот термин называется предикатом суждения и обозначается символом P.

          Следовательно, в общем случае любое  суждение можно представить в виде формализованного предложения, имеющего следующую структуру:

 

                   X = k S m P.                                                                        (1)                                                     

         Эта формула ретроспективно называется основной формулой Канта для простого аналитического суждения.

         Таким образом, при изменении кванторов и мостиков, получаем четыре частных случая суждений:

1) общеутвердительное (позитивное) суждение  A =  S   —  P, которое читается: «все  S обладают свойством P»;

2) общеотрицательное (негативное) суждение  B =   S   –/–   P, которое читается: «все S не обладают свойством P»;

3) частноутвердительное (позитивное) суждение C =   S — P,  которое читается:  «некоторые S обладают свойством  P»;

4) частноотрицательное (негативное) суждение  D =    S  –/–  P, которое читается: «существует  S не обладающее свойством  P».

 

§ 2. Преобразование простых суждений

 

         Простые суждения, имеющие одни и те же термины, называются однородными или унитерминальными. При изменении в таких суждениях видов кванторов и мостиков мы приходим к преобразованиям двух типов, в зависимости от расположения субъектов и предикатов в этих предложениях. В том случае, когда положение субъектов и предикатов не изменяется, преобразования называются репродукциями с указанием изменяемых служебных слов.Для репродукций мы находим три вида преобразований:

1а) репродукция квантора:

         Для этого преобразования получаем:

 —   P) =   S —  P =  C,

 –/–  P)  =   S  –/–  P =  D,      

 —   P) =   S —  P =  A,                                      (2)

 –/–  P)  =   S  –/–  P = B.

2а) репродукция мостика: 

          Для  этого преобразования получаем:

 —   P) =   S  –/–  P = B,

 –/–  P)  =   S —  P =  A,                                   (3)

 —   P)  =    S  –/–  P =  D,

 –/–  P)  =   S —  P =  C.

 

   3а)  Репродукция инверсии.

         Последовательное выполнение двух (или нескольких) преобразований называется их композицией. При композиции репродукций квантора и мостика мы получаем суждение, противоположное по логическому смыслу (и значению) исходному суждению, то есть, инверсию суждения. Таким образом, в классической логике  определяется репродукция инверсии, которая  оказывается композицией первичных репродукций. Репродукцию инверсии высказывания X обозначается двумя основными способами:  или ­­  X. Мы  будем применять первый из этих символов (заметим, что второй из символов обычно применяется при переформулировке суждения для сохранения его семантического содержания). Значит, мы получаем формулу для выражения репродукции через первичные репродукции суждений:

 

                            .                                                      (4)    

        

         Для конкретных видов суждений из этой формулы находим:

          S —  P ) =    S  –/–  P =  D,

 

          S –/–  P)  =  S —  P =  C,

 

           S —  P ) =   S  –/–   P =  B ,                (5)

        

            S  –/–  P ) =   S —  P =  A.

 

          Второй тип унитерминальных преобразований получается в том случае, когда субъект и предикат меняются в предложении местами. Такие преобразования называются трансформациями. Простейшим случаем трансформации является перестановка субъекта и предиката без изменения вида кванторов и мостиков,  это преобразование называется обращением. Все возможные виды трансформаций обозначаются символом  с указанием символа изменяемых служебных слов.

 Для обращения принят символ 

                                      .                                              (6)

Остальные виды трансформаций являются композициями обращения и соответствующих репродукций:

 

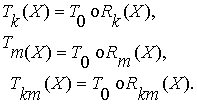                                                                (7)

 

         При выполнении логических преобразований следует следить за сохранением смысла и точностью определения логического значения получаемых высказываний. Рассмотрим более подробно структуру универсума, что позволит   конкретизировать возможности преобразования высказываний.

 

§ 3.  О структуре традиционного Аристотелева Универсума

 

         Восемь основных видов аналитических суждений, как показано в первой главе,  распределяются на три блока, причём второй и третий блоки являются дополнительными и составляют полное покрытие универсума W, а первый блок частично принадлежит как одному, так и второму из них и по своей сути является лишь частичным дополнительным покрытием. Это более подробно будет показано при изучении бинарных операций в следующей главе.

         Репродукции являются первым типом унарных преобразований. При репродукции мостика происходит переход от негативных суждений к позитивным и наоборот, при этом каждый блок универсума является инвариантом преобразования, точнее говоря,  репродукции являются внутренними преобразованиями в этих блоках. Сначала нужно построить общий вид матрицы-столбца для всего универсума, а на его основе выделить вид этой матрицы в каждом блоке. Таким образом, получаем, что исходная матрица имеет вид

 

 

 

 

                                           =     

 

 

 

        

 

Для каждого блока в этой матрице остаются только действующие внутри него элементы, которые и преобразуются с помощью репродукций.

Мы выделим каждый из этих видов, учитывая рабочие элементы блока.

Так, для первого блока  получаем следующий вид матрицы-столбца:

 

 

 

 

 

 

                             =

 

 

 

        

 

 

 

Для упрощения записи здесь иногда пишут только рабочие блоки, хотя сразу надо сказать, что при этом появляется несоответствие между реальным видом матрицы преобразования и его внутренним блочным представлением, что будет показано в следующих параграфах этой главы.

         Учитывая рабочие элементы второго блока  , получим для него свой вид матрицы-столбца из этих элементов:

 

 

 

 

 

                  

 

 

 

                                =      

 

 

 

        

 

         Эти рабочие элементы и подвергаются преобразованиям во втором блоке. По аналогии строим матрицу-столбец для третьего блока

 

 

 

 

 

                           

 

 

 

                          =   

 

 

        

 

                           

                   При этом получаем естественное равенство:

 

                            + = ,

 

Что и является подтверждением правильности покрытия универсума аналитических суждений блоками второго и третьего типа.

 

         § 4. Анализ репродукции мостика.

 

         При репродукции мостика   получаем переход от негативных суждений к позитивным и наоборот.

Так, для первого блока   приходим к виду преобразования:

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                  

 

 

 

 

 

 

                                              

                           

             = 

                                     

 

 

 

 

        

Для второго блока  получаем аналогичную картину преобразования:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                  

                                              

                           

           = 

                                     

 

 

 

 

Таким же образом строится это преобразование и для третьего блока :

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

                  

                                              

 

    =                              

 

 

 

 

 

Итак, мы получили конкретные формулы преобразований репродукции мостика, которые следует научиться правильно использовать. Большого труда это не составляет, так как здесь работает довольно простой алгоритм:

а) сначала определяем расположение заданного суждения в универсуме, то             есть, содержащий его блок,

б) затем по виду суждения строим его репродукцию,

в) по результатам построения находим уровень адекватности суждения.

         Позволим себе некоторые типичные примеры.

         Пусть исходное суждение имеет вид: Х=«В реальности некоторые рыбы являются хищниками». Так как существуют и нехищные рыбы, делаем вывод, что суждение Х принадлежит первому блоку, по строению относится к виду , значит, его репродукция мостика имеет вид , то есть, оно формулируется в виде «В реальности некоторые рыбы не являются хищниками».

 

         § 5. Анализ репродукции квантора

 

         При этой репродукции происходит переход от общих суждений к частным и наоборот, следовательно, здесь особенно внимательно следует контролировать сохранение смысла суждения до и после преобразования. Увлечение только формальными матричными формулами приводит к нарушению самих семантических построений.

         Для первого блока  получаем вид преобразования

 

 

 

 

 

 

                  

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

                                              

                           

   =        

                                     

 

 

 

 

Аналогично, для второго блока   преобразование имеет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 =

  

  

     

   

                                                                                         

                  

                             

                                     

    Теперь  укажем вид этого преобразования для третьего блока  .

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

                  

                                              

 

     =                             

 

 

 

 

 

  В таких преобразованиях особенно внимательным нужно быть к тем случаям, когда частное сильно адекватное суждение превращается в общее сильно адекватное суждение – этот результат в большинстве случаев оказывается неверен.

 

         § 6.  Анализ репродукции инверсии

 

         Инверсия является репродукцией, отражающей композицию репродукций квантора и мостика. Запишем выражения этих преобразований по блокам. Так, для первого блока  получаем:

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                  

                                              

                           

             = 

                                     

 

 

 

 

Аналогично, для второго блока  приходим к преобразованию подобного

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 

    =              

                  

                                                                 

И, наконец, для третьего блока  репродукция инверсии задается матрицей

                                                                                  

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

                  

 

 

 

 

 

 

                                              

        =

                           

 

 

 

    

 

Как уже было сказано раньше, традиционное отрицание является частным случаем репродукции инверсии, поэтому здесь можно пользоваться привычными представлениями о преобразовании. Мы позволим себе не останавливаться на примерах.

 

         § 7. Анализ преобразования обращения и трансформацмии

 

Обращение мы будем рассматривать как своеобразное бинарное преобразование, при котором исходный универсум W преобразуется в универсум   Ŵ, в котором субъект и предикат меняются местами. Он, также как и исходный, подразделяется на три блока, которые также составляют отмеченные ранее покрытия универсума и при всех внутренних преобразованиях, в том числе и при обращении являются инвариантными.

         По известным условиям простого обращения получаем:

а) общепозитивное суждение  типа  А преобразуется в частнопозитивное суждение типа   ,

б) частнопозитивное суждение  типа С преобразуется в частнопозитивное суждение типа  ,

в) общенегативное суждение типа  преобразуется в общенегативное суждение типа ,

г) частнонегативное суждение типа  будем считать преобразующимся  в общепозитивное суждение типа , для первого и второго блоков универсума, а для третьего – в частнопозитивное суждение типа , эта особенность  преобразования согласно общим положениям, выдвинутым ещё Аристотелем, и заставляла логиков отказываться от его применения, хотя, как мы покажем в этом параграфе, при таком определении простого обращения оно в реальности выполняется простым способом и позволяет построить все виды трансформаций как преобразований, являющихся композициями простого обращения и репродукций.

         Теперь мы можем записать вид этого преобразования для каждого из блоков рассматриваемого универсума для случая преобразования обращения.

В результате обращения первый блок исходного универсума становится третьим блоком преобразованного универсума, поэтому для первого блока получаем матричное выражение:         

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

                  

 

 

 

 

 

 

                                              

                           

             = 

                                     

 

 

 

                  

Второй блок является инвариантом  простого обращения, поэтому

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

                  

 

 

 

 

 

 

        

                                     

                           

             = 

                                     

 

 

 

 

Третий  блок в результате простого обращение переходит в первый блок преобразованного универсума

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

                  

 

 

 

 

 

 

                                              

                           

             = 

                                     

 

 

 

 

 

         Трансформации рассматриваются как композиции простого обращения с репродукциями. Они расширяют возможности унарных преобразований и позволяют построить полную их теорию. Мы построим табличные представления всех трансформаций в каждом блоке, так что методика их применения становится совершенно прозрачной.

         Для каждого блока сначала строятся простые обращения, затем репродукции уже преобразованных суждений, и, как результат, сами формулы трансформаций – соответственно, квантора, мостика, а также инверсии.

         Приведем таблицу трансформаций первого блока и рассмотрим для уточнения представления несколько примеров. При этом следует учитывать, что преобразованный в результате простого обращения первый блок оказывается изоморфен третьему, не преобразованному, блоку.

 

                   Трансформации, 1 блок

 

 

Для трансформаций второго блока получаем следующую структурную матрицу:

 

         Трансформации, 2 блок

 

 

 

Аналогичная матрица получается и для трансформаций   третьего блока.

         Трансформации, 3 блок

 

 

 

Итак, мы рассмотрели основные виды унарных операций традиционного Аристотелева семантического универсума.

 

                                            Литература:

 

1.     Schneider M. (и др.) Automatic construction of FCMs// Fussy Sets and Systems, 1998, V.93, (161 – 172).

2.     Евсеев В.И., Вафин Ф.Ф. Моделирование логических форм// «Инициатива – 03», Казань, 2003, (80 – 83)

3.     Евсеев В.И. Моделирование семантических структур // Информационные технологии в системе социально-экономической безопасности России и ее регионов, Казань, 2009, (139 – 146).