Божанов Е.Т.,
Сатыбалдиев О.С., Касымбекова М.Т., Сахабаева А.Р., Койшыбаева Ж.Ж.,
Казахский
национальный технический университет им. К.И. Сатпаева
Токбергенов Ж.Б.
Алматинcкий технологический университет
Движение
нефтегазовой смеси по нефтегазовым трубам под действием критической силы -![]() , когда форма поперечного сечения трапециевидного типа
, когда форма поперечного сечения трапециевидного типа
Пусть математико-гидродинамическое
моделирование резервуара, лежащего на основании типа Винклера под действием критической силы- ![]() приводит к дифференциальному уравнению изогнутой оси
поперечного сечения резервуара[1]-[4] к виду
приводит к дифференциальному уравнению изогнутой оси
поперечного сечения резервуара[1]-[4] к виду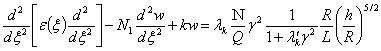
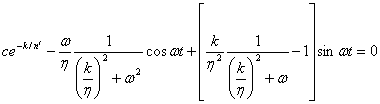 (I)
(I)
нагрузка
упруго – вязкой среды со стороны нефтяной смеси представим в виде модели Фоихта
![]() (1)
(1)
Изменение
плотности поперечного сечения резервуара
на отрезке ![]()
![]() (2)
(2)
При
предположениях:
![]() (3)
(3)
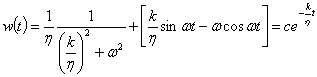
В
следующих случаях:
А) –случай ![]()
B) - случай ![]()
C--случай ![]() ;
;
1.Рассмотрим первое уравнение системы (I) с
учетам на бесконечности
Случай
А)
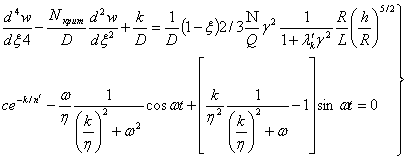 (4)
(4)
При
граничных условиях:
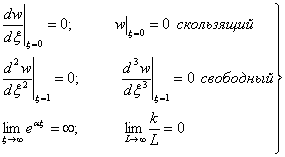 (5)
(5)
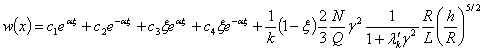 (6)
(6)
На основании граничных условий (5), решая
аналогичным образом (4) получим:
![]() (7)
(7)
Здесь ![]() (8)
(8)
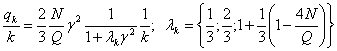 (9)
(9)
![]()
![]()
Построить
график функции из формулы (7)-(9) при следующих данных:
![]()
![]()
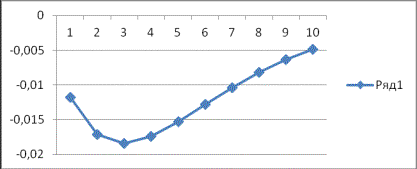
Построить
график функции ![]() из формулы (7) – (9 )
при следующих данных:
из формулы (7) – (9 )
при следующих данных:
![]()
![]()
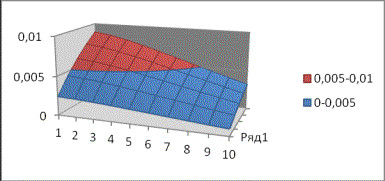
Построить
график функции ![]() из формулы (7) – (9)
при следующих данных:
из формулы (7) – (9)
при следующих данных:
![]()
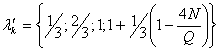
![]()
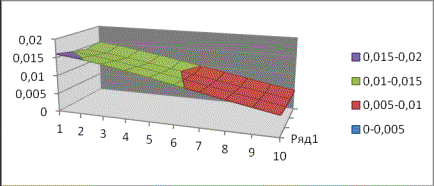
Построить
график функции ![]() из уравнения (4) при
следующих данных:
из уравнения (4) при
следующих данных:
![]()
Построить
график изменения плотности поперечного сечения резервуара на отрезке ![]() при следующих данных:
при следующих данных:
![]() , где
, где ![]()
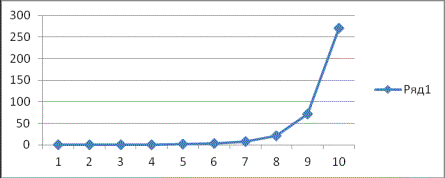
Из данных
конкретного месторождения
![]()
2.
Рассмотрим первое уравнение системы (I) с учетом на
бесконечности
В случае
В)
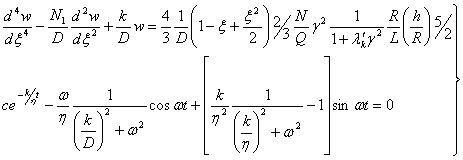 (10)
(10)
При граничных условиях:
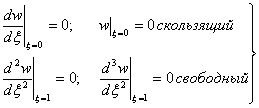 (11)
(11)
Общее
решение:
Корни
характеристического уравнения
![]()
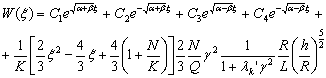 (12)
(12)
На
основании 11 из 12 получим:
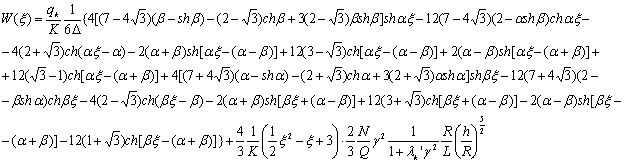 (13)
(13)
Здесь:
![]()
![]() ;
;
![]() (14)
(14)
![]() ;
; ![]() ;
; ![]() ;
; ![]() (15)
(15)
![]() ;
; ![]()
Построить
график функции из формул (13) и (15) при следующих данных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() .
.

Построить график функции ![]() из уравнения (13) и
(15) при следующих данных:
из уравнения (13) и
(15) при следующих данных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]()
![]() , взять
, взять ![]() .
.

Построить график функции ![]() из уравнения (13)-(15)
при следующих данных:
из уравнения (13)-(15)
при следующих данных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
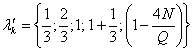
![]()
![]() , взять
, взять ![]() .
.
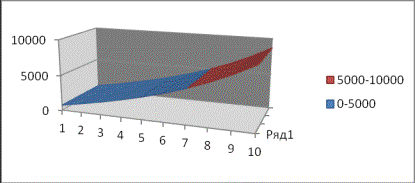
Построить график функции ![]() из уравнения (10) при
следующих данных:
из уравнения (10) при
следующих данных:
![]() ;
; ![]() ;
; ![]() .
.
Замечание. Резервуар, в котором
расположена нефтяная смесь, должен иметь плавно изменяющую непрерывную
поверхность, однако, в местах резкого изменения формы поперечного сечения при
движении нефтегазовой смеси по трубам
от одной насосной станции к другой трем
зонам должен быть плавно изменяющиеся, однако из-за критического пластового давления невозможно избежать резкой
разницы деформации в месте сопряжения. [5],[6]
Тогда, прежде чем решить
основное уравнение изогнутой оси (I) поперечного сечения
необходимо оценить переменные коэффициенты, зависящие от физико-геологических
характеристик и бесконечно малых величин теории приращения. Следовательно,
схему решения системы. (I) необходимо начать с
метода упругих решений. С этой целью
3. Рассмотрим первое
уравнение системы (I) в случае С):
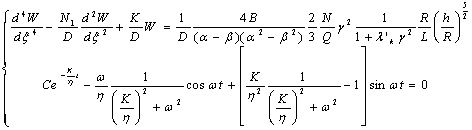 (16)
(16)
При
граничных условиях:
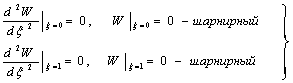 (17)
(17)
Решение: Корни
характеристического уравнения
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; 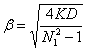 .
.
В нашем случае ![]() ;
; ![]()
Тогда общее решение:
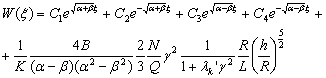 (18)
(18)
На
основании (17) и (18) получим:
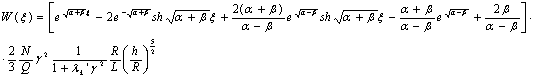 (19)
(19)
При
предположении
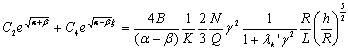 (20)
(20)
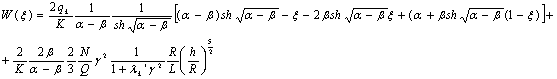 (21)
(21)
При
предположении:
![]() (22)
(22)
![]() ;
;
![]() (23)
(23)
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() , взять
, взять ![]() . (24)
. (24)
Построить
график функции из формул (19) - (24) при следующих данных:
![]()
![]()
![]()
![]()
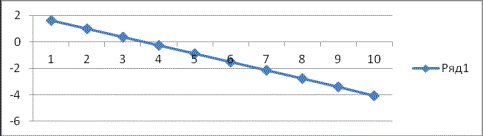
Построить
график функции ![]() из уравнений (19) –
(24) при следующих данных:
из уравнений (19) –
(24) при следующих данных:
![]()
![]()
![]()
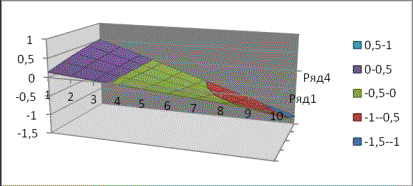
Построить
график функции ![]() из уравнений (19) –
(24) при следующих данных:
из уравнений (19) –
(24) при следующих данных:
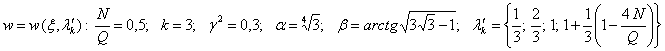
![]()
![]()
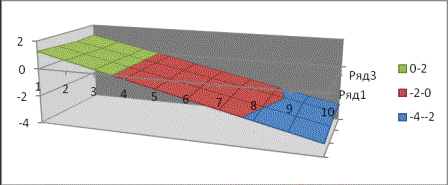
Построить
график функции ![]() из уравнения (16) при
следующих данных:
из уравнения (16) при
следующих данных:
![]()
Выводы:
Резервуар должен иметь плавно изменяющую непрерывную
поверхность, однако в местах резкого изменения формы поперечного сечения или
скачкообразного изменения критического пластового давления невозможно избежать
резкой разницы деформации в месте сопряжения.
Резервуар можно представить в виде гиперболической
градирни при критической нагрузке, размноженной в ряд Фурье вдоль параллели как
функцию напряжения, распределенной по толщине z
поперечного сечения.
Прежде чем интегрировать основное уравнение
многопластового слоя, необходимо оценить переменные коэффициенты, зависящие от
физико-механических свойств и бесконечно малых величин теории приращения.
Схему интегрирования основного уравнения на основании
метода упругих решений необходимо начать с составления модели дифференциального
уравнения изогнутой оси поперечного сечения резервуара за пределами упругости.
Замечание №1.
Если решение (3) при 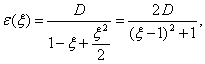 то из первого
уравнения (I) получим:
то из первого
уравнения (I) получим:
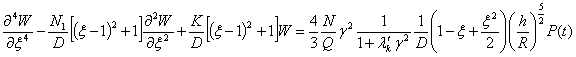
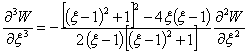
Введем обозначения:
![]() - новые физико-механические характеристики материала
- новые физико-механические характеристики материала
Тогда 
ЛИТЕРАТУРА
[1]. Божанов Е.Т.,Кусаинов
А.А., и др. “Об
устойчивости нефтегазопроводов при действии внутренних сил на стенки
трубопровода трапециевидной эпюры”, Вестник КазГАСА, №2(20), 2006.
[2]. Божанов Е.Т., Ибраимкулов
А.М. и др. “Численные
расчеты выпучивания заполнителя нефтепроводов, транспортирующих вязкие нефти
методом горячей перекачки ”, Материалы международной конференции, КазНТУ, Алматы,
2009г.
[3]. Божанов Е.Т., Ибраимкулов
А.М. и др. “Надежность
технологического потока перекачки на основании математико-компьютерной модели
”,II-ая международная научно-практическая конференция, КазНТУ,
том I, Алматы, 2011г.
[4]. Божанов Е.Т., ОтарбаевЖ.О.,
Буганбаева С.Н.“Механико-математическое
моделирование нефтепроводов, транспортирующих вязкие нефти методом горячей
перекачки”, Труды международного форума “Наука и инженерное образование без
границ”, КазНТУ, том I, Труды международного
форума и наука и инженерное образование без границ, Алматы, 2009г.
[5]. Божанов Е.Т., Джунисов А.Т., Акимжанова
Ш.А.“Математическая модель движения нефтегазовой смеси по стволам траектории
скважины под действием технологического критического давления в N-ом горизонте
гомогенного пласта большой мощности”, Труды II-международной научной
конференции“Высшие технологии – залог устойчивого развития”, КазНТУ, том II,
Алматы, 2013г.
[6]. Божанов Е.Т., Ибраимкулов А.М., Койшыбаева
Ж.Ж., Касымбекова М.Т.“Выпучивание симуляционной модели резервуара в
зависимости от вида критической силы по форме критической деформации
трапециевидной формы и гиперболические тонкостенные градирни. , Materialy IX Mezinarodni Vedecko –Praktika Konferece.,Zpravy
Vedecke IJEZE-2013, D/L
22, Praha, Publishing House
«Education and Science»,
s.r.o.