А.Н.Сагдатдинова

ЛПИ - филиал СФУ, Лесосибирск

Аффинное преобразование как метод решения геометрических задач

Геометрия, изучаемая в школьном курсе, является геометрией группы подобий. Преобразования движения и подобия оставляют все существенные свойства геометрических фигур неизменными и применение их к решению задач достаточно подробно исследовано. Вместе с тем существуют геометрические задачи и теоремы, при решении и доказательстве которых достаточно учитывать лишь свойства, сохраняющиеся при аффинных преобразованиях.

Исходя из основных инвариантов аффинных преобразований, можно предположить следующую классификацию задач:

1) задачи на коллинеарность точек;

2) задачи на конкурентность прямых;

3) задачи на параллельность прямых;

4) задачи на пропорциональность отрезков;

5) задачи отношение площадей.

Суть метода аффинных преобразований состоит в следующем: предположим, что геометрическая задача сводится к некоторой конфигурации F. Если произведем аффинное преобразование плоскости чертежа, то конфигурация F перейдёт в конфигурацию F, которая может быть проще конфигурации F и построение которой может быть легко выполнено. Тогда решаем задачу в преобразованном виде в конфигурации F' и, произведя обратное преобразование чертежа, получаем искомое решение задачи. [2]. Таким образом, решение задач данным методом предполагает выполнение следующих действий:

· вместо данной фигуры рассматривают ей аффинно-эквивалентную, но более простой формы;

· решают задачу для этой более простой фигуры, используя её свойства;

· распространяют с помощью аффинного преобразования полученный результат на заданную фигуру.

Продемонстрируем алгоритм на примере решения задачи:

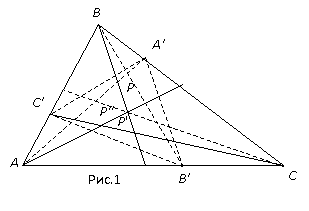
Точки А', В' и С' делят соответственные стороны ВС, СА и АВ треугольника АВС в одном и том же отношении. Доказать, что при этом точка Р пересечения медиан треугольника АВС, точка Р' пересечения медиан треугольника А'В'С' и точка Р'' пересечения медиан треугольника, образованного прямыми АА', ВВ' и СС', совпадают.

Доказательство. Любое аффинное преобразование, преобразующее один треугольник в другой, преобразует медианы одного треугольника, а с ними и точку их пересечения, соответственно в медианы и точку пересечения медиан другого треугольника.

2516674562516664322516654082516643842516633602516623362516592642516613122516602881. Зададим аффинное преобразование тремя точками А,В,С и их образами В,С,А. Тогда треугольник АВС преобразуется в треугольник ВСА, а точка Р пересечения медиан будет неподвижной точкой этого преобразования. При этом и треугольник А'В'С' также преобразуется в себя так, что точки А',В',С' перейдут соответственно в точки В',С',А', а точка пересечения медиан треугольника А'В'С'- точка Р' также перейдёт в себя.

2. Данное преобразование не является родством так как прямая АВ не параллельна прямой ВС, а эти прямые соединяют точки, соответственные в данном преобразовании.

3. Значит, построенное нами аффинное преобразование не может иметь две различные неподвижные точки., а поэтому точки Р и Р' должны совпасть. С другой стороны, ВС, В'С', так что прямая ВВ' преобразуется в прямую СС' (рис.1). Прямые СС' и АА' преобразуются соответственно в прямые АА' и ВВ'.

4.Отсюда следует, что и точка Р'' неподвижная и, значит, совпадает с Р и с Р'.

Метод решения задач с помощью аффинных преобразований:

- позволяет перейти от более сложной конфигурации к более простой для осуществления процесса решения;

- имеет широкую область применения, но чаще всего используется при решении задач на отношение площадей;

- осмысление и применение данного метода формирует конструктивный подход к решению задач и критичность мышления.

Список литературы:

1.Понарин, Я. П. Элементарная геометрия [текст]: В 2 т. – Т. 1/ Я.П.Понарин– М.: МЦНМО, 2004. – 312 с.

2.Ходот, Т. Г. Задачи по геометрии [текст] : учеб. пособие для студ.высш.пед. учеб.заведений/ Т. Г. Ходот, И. Д. Захарченко, А. Б. Михайлова. – М.: Издательский центр «Академия», 2006.- 256 с.

3.Четверухин, Н. Ф. Проективная геометрия [текст] : учеб. пособие –издание 6-е/ Н.Ф. Четверухин– М.: Государственное учебно – педагогическое издательство министерства просвещения РСФСР, 1953.