О.В. Матысик, к.ф.-м.н., доцент

Брестский государственный университет имени А.С. Пушкина (Беларусь)

НЕЯВНЫЙ МЕТОД ИТЕРАЦИЙ РЕШЕНИЯ НЕКОРРЕКТНЫХ ЗАДАЧ С НЕСАМОСОПРЯЖЁННЫМ ПРИБЛИЖЁННЫМ ОПЕРАТОРОМ В СЛУЧАЕ АПОСТЕРИОРНОГО ВЫБОРА ПАРАМЕТРА РЕГУЛЯРИЗАЦИИ

Пусть H и F – гильбертовы пространства, A L   (H, F), т. е. А – линейный непрерывный оператор, действующий из H в F. Предполагается, что нуль не является собственным значением оператора А, однако нуль принадлежит его спектру. Рассмотрим линейное операторное уравнение

(1)

Задача отыскания элемента по элементу является некорректной, так как сколь угодно малые возмущения в правой части y могут вызывать большие возмущения решения уравнения. Предполагаем, что точное решение уравнения (1) существует и является единственным. Будем искать его с помощью итерационного метода

, (2)

где E – тождественный оператор, – итерационный шаг. Считаем, что оператор А и приближённая часть y уравнения (1) заданы приближённо, т. е. вместо y известно приближение , , а вместо оператора известен оператор , . Предполагаем, что и . Тогда приближения (2) примут вид

. (3)

Пусть , , , , . Неявная итерационная процедура (3) запишется в виде , где

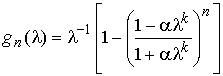. При для выполняются условия:

, , (),  (4)

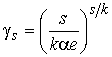, (), , , (5)

(здесь – степень истокообразной представимости точного решения , , ),

, , (), (6)

, . (7)

Докажем сходимость метода (3) в случае апостериорного выбора параметра регуляризации при решении уравнения (1) с несамосопряжённым приближённым оператором, получим оценку погрешности метода и оценку для апостериорного момента останова.

Зададим уровень останова и определим момент останова итерационного процесса (3) условием

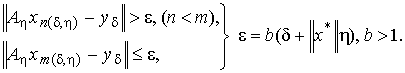(8)

Предположим, что при начальном приближении невязка достаточно велика, больше уровня останова , т. е. .

В случае несамосопряжённого оператора метод (3) примет вид

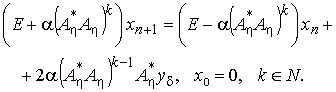(9)

Покажем возможность применения правила останова по невязке (8) к методу итераций (9). Справедливы

Лемма 1. Пусть L (H, F), , и выполнено условие (5) с . Тогда при где . Если то при

Лемма 2. Пусть L (H, F), , и выполнены условия (5), (7). Если для некоторого и имеем или при , то .

Теорема 1. Пусть L (H, F), , , и выполнены условия (5), (6) с . Пусть параметр выбран по правилу (8). Тогда при , .

Теорема 2. Пусть выполнены условия теоремы  1. Если то справедливы оценки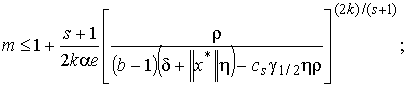

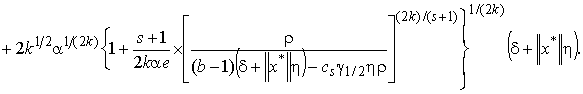(10)

Замечание 1. Порядок оценки (10) есть , и он оптимален в классе задач с истокопредставимыми решениями. В оценке погрешности (10) (c_s ≤ 2 для 0 < s ≤ 1).

Замечание 2. Знание порядка и истокопредставляющего элемента z, используемое в теореме 2, на практике не потребуется. При останове по невязке (8) автоматически делается нужное число итераций для получения оптимального по порядку решения.