УО ФПБ
«Международный университет «МИТСО»», Беларусь
К вопросу организации
самостоятельной работы в вузе, в процессе изучения высшей математики
Самостоятельная работа студента – это основа его
образования, а для студентов заочной формы обучения самостоятельная работа
играет особую роль на протяжении всего периода их обучения в ВУЗе. Через
выполнение самостоятельных работ у обучаемого формируется готовность к
самообразованию, возможность постоянно повышать свою квалификацию, а если
возникает необходимость, то и получении новых профессиональных знаний и навыков.
Исходя из современных требований любой молодой
специалист должен обладать фундаментальными знаниями, профессиональными умениями,
а так же опытом творческой и исследовательской деятельности по решению задач
возникающих в профессиональной сфере деятельности. Навыки решения нестандартных
профессиональных задач формируется в основном в процессе самостоятельной работы
студентов.
Высшая школа отличается от средней не только
узкой специализацией, но главным образом методикой обучения и высокой степенью
самостоятельности обучаемых. Преподаватель ВУЗа должен грамотно и рационально
организовать учебную деятельность студента, при этом студент должен в большей
степени самостоятельно получать необходимые знания.
Всякая самостоятельная работа преследует
несколько целей одновременно:
Первая – это овладение нужной дисциплиной, в
нашем случае высшей математикой, а вторая – это формирование приемов и навыков
самостоятельной работы в учебной, научной и профессиональной деятельности, а
так же способности принимать на себя ответственность за самостоятельное решение
проблемы. Заметим, что самостоятельная работа как метод обучения выходит далеко
за рамки отдельного предмета, так как через навыки приобретенные через
самостоятельное получение знаний – формируется многие профессиональные
компетенции будущего специалиста. Поэтому необходимо в рамках отдельного
предмета разрабатывать стратегию формирования системы умений и навыков
самостоятельной работы.
Основная трудность у студентов первокурсников
при изучение высшей математики – это отсутствие навыков самостоятельной работы.
Значит каждый преподаватель должен помочь студенту наиболее эффективно организовать
свою учебную деятельность. Однако нужно заметить, что основную работу,
связанную с овладением знаниями, студент должен проделать самостоятельно. Так
же для успешного выполнения самостоятельной работы необходимы: четкое
формулирование заданий, логическая связь между задачами, предлагаемых для
самостоятельного обучения, и обязательное указание справочной и учебной
литературы, которой может пользоваться студент, при этом очень важную роль
играет своевременный и объективный контроль за работой студента со стороны
преподавателя.
Достигнуть высоких целей при изучении высшей
математики можно только соединив обучение под руководством преподавателя и
собственную познавательную деятельность студента.
Основное назначение самостоятельной работы в
ВУЗе – развитие навыков самообразования. Основной вид деятельности студента при
изучение высшей математики – это решение задач или выполнение практических
заданий. В процессе такой работы студент овладевает знаниями, умениями и
навыками и различными способами учебной деятельности. Существует ряд
объективных трудностей, которые мешают студентам заочникам освоить программу по
высшей математике, к сожалению, многие не владеют основными математическими
понятиями, не умеют находить нужные подходы к решению задач, так как у них не
сформированы общие умения решения математических задач. Поэтому необходимо
организовать самостоятельную работу студента-заочника так, что бы она
способствовала адаптации к обучению в ВУЗе, и самое главное, помогала
вырабатывать умение и навыки в решении различных поставленных задач. Если
придерживаться такого подхода, то это способствует углублению и расширению
знаний студентов-заочников и развитию у них общеучебных и профессиональных
умений. Рассмотрим самостоятельную работу студента в каждой форме учебного
процесса. На установочных занятиях, а это в основном лекции, самостоятельная
работа осуществляется под руководством преподавателя, и сводится на этом этапе
к самоконтролю и самооценки студента. На практических занятиях самостоятельная
работа необходима для глубокого изучения отдельных теоретических положений,
методов и способов решения математических задач. Наибольшее значение в процессе
изучения высшей математики, имеет правильная организация самостоятельной работы
студентов в период их подготовки к зачетной-экзаменационной сессии. В данный
период студент должен, практически самостоятельно, изучить учебный материал,
предусмотренный программой и подготовиться к сдаче зачета или экзамена в
соответствии с учебным планом. Именно на этом этапе обучение студентам
необходимо консультативная помощь преподавателя. Рассмотрим некоторые методы и
приемы организации самостоятельной работы студентов в период подготовки к
зачетно-экзаменационной сессии. Во
время установочных занятий преподаватель ориентирует студентов по организации
учебного процесса в ВУЗе и студенты должны иметь возможность познакомиться с
учебными планами, программой по высшей математике, требованиями к зачету и
экзамену, правилами проведения зачета и экзамена, а так же знать какими
основными знаниями и умениями они должны овладеть при изучение предмета.
Студентам необходимо предложить список учебно-методической литературы с
краткими пояснениями и подробными рекомендациями преподавателя. Так же
студентам целесообразно предлагать разработки практических занятий по программе
с подбором задач по каждой теме, при этом для типовых задач целесообразно
приводить образцы их решений. Очень важным моментом является предложение
системы задач для самостоятельной
работы, которая поможет студентам изучить основные разделы программы. К
заданиям необходимо приложить методические рекомендации по решению, а так же
можно приложить тестовые задания различных уровней для промежуточного контроля.
Основная часть заданий, которая предлагается студентам для самостоятельной работы
- это типовые задачи решение которых
можно выполнить по образцу. Для удобства студенты могут ознакомиться с
решениями предложенных типовых, демонстрационных задач. Перед изучением
демонстрационных задач студенты должны повторить необходимые теоретические
материалы, для этого составляется перечень вопросов, ответы на которые можно
найти в указанной учебной литературе. Итогом выполненной работы является
разноуровневые тесты, которые обучаемые должны выполнить самостоятельно.
Используя данный подход покажем, как студенты
могут изучить тему «Пределы»
1)
Используя
литературу (Письменный Д.Т., Конспект лекций по высшей математике (полный
курс), Москва, 2007 год) повторить основные понятия темы.
2)
Рассмотреть
демонстрационные примеры
Найти
предел последовательности: 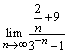 .
.
Применим теорему о переходе к пределу в
равенствах:
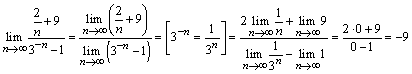 .
.
Найти
предел последовательности: ![]() .
.
Так как последовательности {n2 + n - 5} и ![]() расходящиеся, то применять теорему о переходе
к пределу в равенствах здесь нельзя.
расходящиеся, то применять теорему о переходе
к пределу в равенствах здесь нельзя.
Поэтому преобразуем дробь ![]() .
Определим старшие степени n
числителя и знаменателя (в данном примере это n2 и n)
и вынесем их за скобки.
.
Определим старшие степени n
числителя и знаменателя (в данном примере это n2 и n)
и вынесем их за скобки.
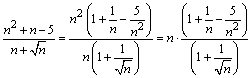 . Тогда
. Тогда
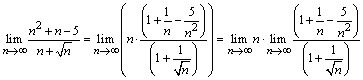 . Первый предел равен
бесконечности, а второй 1, поскольку
. Первый предел равен
бесконечности, а второй 1, поскольку 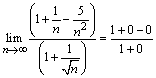 .
Следовательно,
.
Следовательно, ![]() .
.
3)
Решить
тестовые задания
1.
Найти
предел последовательности ![]() ;
;
·
+![]() ;
;
·
-∞;
·
-0;
·
-1;
·
-4.
2.
Найти
предел последовательности 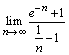 ;
;
·
+-1;
·
-∞;
·
-0;
·
-1;
·
-2.
Литература
1.
Тишков
К.Н., Кошелев О.В,, Мерзляков И.Н., Роль и методы самостоятельной работы
студентов в современных условиях, Нижний Новгород, НГТУ, 2008 год