Педагогические науки. Проблемы подготовки специалистов.

Нестеренко В.О., Саппа Ж.В., Лихачов Д.

Харківський національний автомобільно-дорожний університет

ПРО САМОСТІЙНУ РОБОТУ СТУДЕНТІВ ВТУЗІВ

ПРИ ВИВЧЕННІ ВИЩОЇ МАТЕМАТИКИ

Розглянемо організацію та контроль самостійної роботи студентів на прикладі вивчення теми «Перетворення Лапласа». Ця тема є однією з останніх тем курсу вищої математики у підготовці студентів технічних спеціальностей другого курсу. Для опанування цією темою студентові необхідно прикласти чималі зусилля, оскільки треба знати попередні розділи вищої математики (диференціальне та інтегральне числення функції однієї змінної, функції багатьох змінних, кратні та криволінійні інтеграли, диференціальні рівняння, теорію функцій комплексної змінної). Для цього потрібно активізувати самостійну роботу студентів.

Перетворення Лапласа широко застосовується у самих різних галузях науки і техніки. Особливо важливу роль воно грає при дослідженні перехідних процесів у лінійних фізичних системах електротехніки, електроніки, механіки та у інших галузях знань. Сучасних математичний апарат перетворення Лапласа (операційного числення) дозволяє розв’язувати проблеми, які описуються системами лінійних диференціальних рівнянь (як звичайних так і з частинними похідними). Така велика універсальність метода пояснюється його ефективністю – можливістю одержати розв’язок деяких завдань найбільш простими й економічними шляхами.

Самостійна робота студентів є важливою складовою при вивченні вищої математики. Впровадження міжнародних стандартів освіти передбачає удосконалення форм і методів організації самостійної роботи студентів. Крім того, це форма організації навчального процесу, відповідно до якої заплановані завдання виконуються в поза аудиторний час. Самостійна робота повинна сприяти формуванню у студентів навичок планувати й регулювати свою діяльність. У цій діяльності на перше місце виходить робота студентів під керівництвом викладача, оскільки, як бачимо, обсяг знань, який використовується, великий. Викладач має не тільки видати студентам навчальні завдання для виконання індивідуальної роботи, але і сформувати у них зацікавленість додатково займатися для досягнення високого рівня своїх знань, тобто, викладач повинен створити ефект мотивації самостійної роботи.

Зокрема, у Харківському Національному Автомобільно – Дорожньому Університети для активізації самостійної роботи студентів при вивчені теми «Перетворення Лапласа» розроблений пакет навчальне – методичного забезпечення, який складається з конспекту лекцій, методичних вказівок до виконання типових завдань і самостійної роботи студентів, завдання для перевірки рівня засвоєння окремих частин теми, тест для контролю рівня знань по темі.

Для поглибленого засвоєння розділів теми нами практикується індивідуальна робота – написання рефератів, або доповіді по окремих розділах теми, наприклад: « Застосування інтеграла Дюамеля», «Розв’язання лінійних диференціальних рівнянь зі сталими коефіцієнтами операційним методом». Типові завдання складені таким чином, щоб варіанти були однакого рівня складності, питання в якому розташовані у зростаючому рівні складності.

Використання пакету навчальне – методичного забезпечення передбачає розвиток творчого та аналітичного мислення студентів, вміння виділяти головне, активізувати систематичну самостійну роботу протягом усього семестру. Для підвищення ефективності навчання, процес викладання теми зорієнтований на формування у студентів наукових понять та прийомів виконання розумових дій, а пізнавальна самостійність студента має бути наслідком рівня оволодіння ним змістом теми та вмінням її вивчати. Завдання для самостійної роботи складені таким чином, щоб вони охоплювали усі розділи теми.

Конспект лекцій та методичні вказівки можуть бути у нагоді для студентів – магістрів й аспірантів, які використовують тему «Операційне числення».

Надамо типовий варіант самостійної роботи студентів по темі « Перетворення Лапласа».

1. За оригіналом знайти його зображення:

а); б) ; в) ;

г) ; д) .

2. Записати згортку функцій та знайти її зображення:

( згортка функцій визначається рівністю )

а) (t)=; б) .

3. За теоремою про згортку знайти оригінал по зображенню:

а) ; б) .

4. Знайти зображення періодичної функції , яка має період і на періоді задається функцією

.

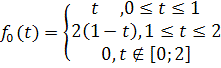5. Для заданих зображень знайти оригінали:

а) ; б) .

6. Розв’язати диференціальне рівняння операційним методом, якщо задані початкові умови:

.

7. Розв’язати систему диференціальних рівнянь:

.

Розглянемо одну з реферативних тем, а саме «Застосування інтеграла Дюамеля».

Нехай задане лінійне диференціальне рівняння 2-го порядку зі сталими коефіцієнтами та довільною правою частиною і нульовими початковими умовами

де L – диференціальний оператор. Крім цього розглянемо рівняння з нульовими початковими умовами. Розв’язок цього рівняння позначимо через (t), а його зображення – через Тоді в операційній формі має вигляд де характеристичний многочлен. Вважаючи відомими (t) та знайдемо . Рівняння в операційній формі має вигляд

звідки

.

Застосуємо інтеграл Дюамеля і, зважаючи на початкові начальні умови, дістанемо Особливість цього методу полягає у тому, що для знаходження не треба знати

Приклад. Розв’язати задачу Коши: Розв’язання. Зазначимо, що функція у правій частині при інтегруванні не виражається через елементарні функції. Розв’яжемо допоміжне рівняння У операторній формі , або .

Далі, за інтегралом Дюамеля, знаходимо розв’язок у вигляді

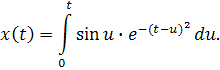
Література

[1] - Нестеренко В.О. Методичні вказівки до виконання типових завдань і самостійної роботи (тема: «Операційне числення») / В.О.Нестеренко, Ж.В.Саппа // Харків: Вид-во ХНАДУ. - 2002. – 37с.

[2] - Пак В.В. Вища математика / В.В.Пак, Ю.А.Носенко // К .: Либідь, 1996. – 440 с.

[3] - Саппа Ж.В. Операційне числення. Конспект лекцій / Ж.В.Саппа // Харків: Вид-во ХНАДУ. - 2001. – 24с.