Физика/1.Теоретическая физика

 

Д.ф.-м. н., профессор Юденков А.В. 1,

к.ф.-м. н. Володченков А.М.2,

к.ф.-м. н.  Скородулина Е.Ю. 2

 

1. ФГБОУ ВПО «Смоленская ГСХА», Россия

2.ФГБОУ ВПО «Смоленский филиал РГТЭУ», Россия

 

Стохастическая краевая задача Гильберта для бианалитических  функций

 

Дадим классическую постановку краевой задачи Гильберта для бианалитических функций [1].

Пусть D односвязная  область, ограниченная контуром Г. Требуется найти бианалитическую в области D функцию

                                                 (1)

по краевым  условиям

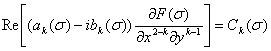,                                 (2)

         Здесь  – аналитические компоненты; , , – заданные на контуре Г действительные функции. Будем считать, что выполнены условия нормировки 

Классическая задача Гильберта для бианалитических функций была рассмотрена в работах В.С.Рогожина, М.П.Ганина, К.М. Расулова. Достаточно полно основные методы решения задачи (2) и ее обобщений приведены в работе [5].

Задача Гильберта для бианалитических функций (2) моделирует напряженное состояние упругого изотропного тела в случае, когда нагрузки, форма тела, упругие характеристики могут быть представлены детерминированными функциями [3]. Однако, во многих практических задачах указанные параметры носят случайный характер. Поэтому актуальной научной задачей является изменение постановки и методов решения задачи Гильберта таким образом, чтобы с ее помощью можно было определять случайные бианалитические функции.

В работе предлагается выразить решение задачи Гильберта для бианалитических функций в терминах броуновского движения. Этот подход соединяет теорию краевых задач для бианалитических функций с вероятностной теорией потенциала [2].

Сформулируем  понятие Х –  бианалитических функций.

Определение 1. Функция  в области D ограниченной контуром Г называется Х- бианалитической, если для всех  и всех открытых множеств W, для которых , аналитические компоненты  и  представимы в следующем виде

, k=0,1     (3)

Здесь  – математическое ожидание случайной функции, – момент первого выхода двумерного броуновского процесса из множества w. Функции  и  связаны между собой соотношения Коши-Римана.

         Лемма 1. Пусть F – X- бианалитическая функция в области D плоскости комплексного переменного z, A – характеристический оператор, тогда

.                                                         (4)

Обратно, если  и  в D, то функция F является Х- бианалитической.

Доказательство.

Применим дважды к функции  характеристический оператор.

,

.

         Для доказательства обратного утверждения воспользуемся формулой Дынкина.

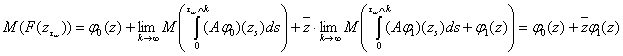       Для дальнейших исследований понадобиться следующее утверждение (см [4] стр. 216).

 Лемма 2. Пусть  – ограниченная измеримая функция на границе Г области D.

         Тогда функция  является гармонической.

Рассмотрим задачу Гильберта в стохастической постановке, ограничившись случаем круговой области.

         Требуется найти  Х – бианалитическую функцию по краевому условию на единичной окружности L, ограничивающей круговую область D.

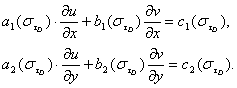                                              (5)

         Здесь  – первый момент выхода двумерного броуновского процесса из области D,  – действительные функции, заданные на контуре L, удовлетворяющие условия Гильберта вместе со своими производными;  , – действительные функции удовлетворяющие условию Гельдера вместе с производными до (3-к) порядка включительно.

         Граничные условия (5) выполняются почти наверное.

Учитывая, что

                             

краевые условия (5) можно привести к следующему виду

,                           (6)

.

         Сведем стохастическую задачу Гильберта для бианалитических функций к четырем стохастическим задачам Дирихле для X-аналитических функций.

         Найдем регуляризирующие  множители для задачи (6). Для этого решим следующую вспомогательную задачу

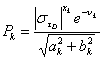,                                                        (7)

,

где  .

         Второе условие (7) представляет собой стохастическую задачу Дирихле для аналитических (гармонических) функций. Существование и единственность

регуляризирующего  множителя обеспечивается единственностью и существованием решения стохастической задачи Дирихле для гармонических функций.

Перейдем к решению стохастической задачи Гильберта для бианалитических функций.

         Воспользуемся тем, что на окружности выполняется условие

                                                                (8)

         Введем вспомогательные аналитические функции

,                                        (9)

         Перепишем краевые условия (6) в следующем виде

,                                          (10)

                                                   .     

         Пусть – регуляризирующие  множители функций . Преобразуем уравнение (10)

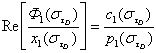,                                              (11)

.

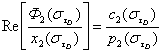         Краевые условия (11) представляют собой стохастические задачи Дирихле. Решение задач дается формулами [4].

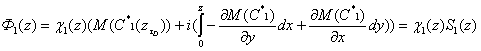,                            (12)

.

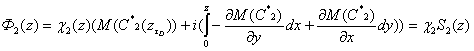Здесь    (k=1,2).

         Искомые Х-аналитические функции найдем по формулам

,                                                (13)

.

         Пусть теперь >0. В этом случае аналитические функции  имеют в начале координат полюс порядка . В этом случае

.                                           (14)

         Здесь ;– произвольные  комплексные постоянные.

         Пусть <0. В этом случае стохастическая задача Гильберта для Х-бианалитических функций безусловно разрешима в том, случае, если допустить, что искомые аналитические компоненты имеют в начале координат полюсы определенных порядков.

         Разложим функцию  в ряд Тейлора в окрестности точки z =0.

                                   (15)

         Для разрешимости задачи Гильберта необходимо и достаточно выполнения условий

,  ,                                            (16)

         Положим

 (j=1,…, )                                                  (17)

                                                   

         Действительная часть функции  является гармонической функцией. Значит, она представима рядом Тейлора

.                                          (18)

         Здесь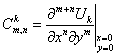  

         Условия (17) будут равносильны следующим условиям

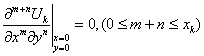                                      (19)

или

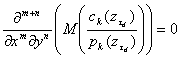                                           (20)

         Случай, когда индексы краевых коэффициентов имеют разные знаки можно исследовать аналогично.

         Сформулируем итоговый результат.

         Теорема. Стохастическая задача Гильберта для бианалитических функций на окружности сводится к решению двух стохастических задач Дирихле для определения регуляризирующих множителей и двух независимых стохастических задач Дирихле для определения искомых аналитических компонент.

         Число линейно независимых решений однородной задачи l и число условий разрешимости неоднородной задачи v связаны с индексами краевых коэффициентов соотношением

,                                       (21)

т.е. стохастическая задача Гильберта для бианалитических функций является нётеровой.

         Схема решения стохастической задачи Гильберта для бианалитических функций не меняется, если область D, отображается на внутренность единичного круга рациональными функциями.

 

Литература:

1.     Гахов Ф.Д. Краевые задачи. – М.: Наука, 1977, 640 с.

2.     Дынкин Е.Б. Основание теории марковских процессов. – М. ФИЗМАТЛИТ, 1959, 226 с.

3.     Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: Наука, 1966, 511 с.

4.     Оксендаль Б. Стохастические дифференциальные уравнения. – М.: «Мир», 2003. – 406 с.

5.     Юденков  А.В.,  Володченков  А.М.  Основные  задачи  теории  упругости  тел  с прямолинейной анизотропией в стохастической теории потенциала //Ученые записки: электронный научный журнал Курского государственного университета . 2013. № 2 (26) [Сайт]. URL: http://scientific-notes.ru/pdf/030-002.pdf