A. L’vov,
M. Svetlov and Yu. Ulyanina
Saratov State Technical
University named after J.A.Gagarin
Research of noise immunity of pseudo-random sequences
in the non-binary
communication channels
Abstract
In modern digital systems of transmission
measuring and control information main problem is the securing of noise immunity
of the channel signals. Result of analysis of the many various methods and algorithms
of information transfer in previous
works authors – the best channel signals for noise immunity in the non-binary
communication channels is pseudorandom signals (PRS).
In this paper analytical relationships
between noise immunity of the PR- sequences and their statistical properties
are discussed.
Results of the researches of the PR-sequences
which basing on the new introduced code metric show the new
possibilities of the estimations of the
channel signals noise immunity.
Keywords: pseudo-random sequence, communication
channel, correlation, non-binary signal, noise
immunity.
1. INTRODUCTION
Noise immunity of any data transmission system, including systems using
PRS is characterized by the redundancy coefficient [1, 2]. From a practical
point of view, the problem of determining the relationship between the
properties of the used codes’ noise immunity (coefficients of redundancy) and
their statistical properties (normalized autocorrelation coefficients) is
fundamentally important when constructing noise proof information channels that
use non-binary PRS codes. The analysis showed that in the classical coding
theory, such relationships are not available.
This paper presents the evaluation of metric characteristics of
non-binary PRS that are different from the classical ones by the greater degree
of realization of the PRS noise immunity potential; the equations for
calculating the correlation and spectral characteristics of the non-binary code
PRS with the proposed code metrics are obtained; the formula for calculating
the coefficients of code redundancy by the minimum distance, multiplicity of
the deletion or transformation error correction, by the normalized
autocorrelation coefficients and a priori statistical characteristics for
channels with transformation or deletion errors are proposed.
2. REDUNDANCY EVALUATION OF THE CODE REPRESENTED BY THE NON-BINARY PR-SEQUENCES
2.1. Channels with
transformation errors
As known, code noise immunity is characterized by the redundancy factor.
It is possible to define the code statistical characteristics, namely the
normalized coefficients of the autocorrelation function (ACF), in the terms of
redundancy factors using the relationship for redundancy borders. In codes’
synthesis for the channels with transformation errors the most widely used
relationships for borders redundancy are Hamming, Varshamov-Gilbert (for codes,
which code length is much higher than the number of data symbols, that is, for
codes with high redundancy), and Plotkin (for low-speed codes) [3]. Analysis of
these relationships yielded algorithms for calculating the factors of code
redundancy using minimum code distance, a number of transformation error
corrections and normalized autocorrelation function coefficients, taking into
account the introduced metric of non-binary code PR-sequences. Algorithms for
calculating the coefficients of code redundancy R through normalized autocorrelation function coefficients can be
written as follows:
a)
using
Hemming border redundancy:
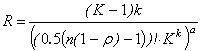; (1)
were 
;
b)
using Varshamov-Gilbert border redundancy:
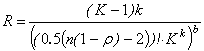; (2)
were 
;
c)
using Plotkin border redundancy:
. (3)
In (1) - (3) k is the number
of code check symbols, K is the code
base.
From the expressions (1) - (3) it is easy to get the relationship
between the factors of code redundancy R,
the number of transformation error correction s and the value of minimum code distance dmin that coincides with the value d in equation 
and 
.
2.2. Channels with erase
errors
In practice, besides the channels with transformation errors one often
comes across the channels with erase errors. In the article the authors [4],
based on the analysis of mathematical models of such channels the classic
formula for the lower bound of redundancy Hamming converted to a form that
takes into account the peculiarities of erasure channels:
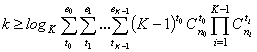, (4)
\where n0 is the
number of zero codeword symbols; ni
are the numbers of non-zero codeword symbols; e is the value of erase error correction multiplicity; e0, e1, …, eK-1
are the values of corresponding characters erase error correction multiplicity.
With regard to equation (4) the algorithms for calculating the factors
of code redundancy using the values of minimum code distance, the multiplicity
of erase error correction, and normalized autocorrelation function
coefficients, taking into account the introduced the non-binary code
PR-sequence metric for the channels with erase errors were obtained:
a)
dependence of code redundancy on normalized
autocorrelation function coefficients:
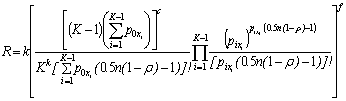, (5)
where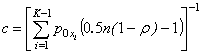 
; 
; 
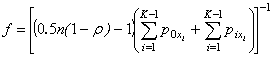is the probability of erase error in the null symbols; 
are the
probabilities of erase error in symbols i
(i = 1,2,...K –1);
b)
the other dependencies can be obtained by
substituting 
and 
in (5).
These dependences are valid for asymmetric channels, but in practice
symmetrical channels are often considered when modeling. The above results are
adapted to the case of a symmetric channel. Symmetrical is the channel in which
the following equalities are satisfied:
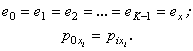(6)
With these equations the formula for the low redundancy (4) takes the
following form:
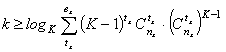. (7)
From the expression (7) the minimum value of k (the number of control bits of code) can be determined. Then the
relationship between the coefficients of code redundancy and normalized
coefficients of the autocorrelation function can be written as:
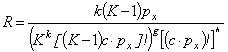, (8)
were 
; 
.
Dependencies
and 
for symmetrical K-ary
channel are synthesized in the same manner as for the asymmetric channel.
Analysis of the relations shows that the probability of correct
reception of non-zero symbols significantly higher than the probability of
correct reception of null characters, so it is advisable to use the codes
without the use of zero-tale signs.
In this case, the formula for the low redundancy can be represented as
follows:
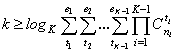. (9)
The relationship between the coefficients of code redundancy and the
coefficients of normalized
autocorrelation function is:
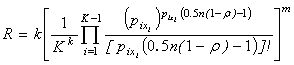, (10)
were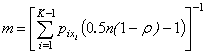 
.
Today, the most common option of K-ary
codes is the ternary code. Substituting in the above formulas K = 3 
, 
and 
can be obtained, for
symmetrical and asymmetrical ternary channels with and without the null
character.
3. Evaluation
of redundancy using a priori statistical characteristics
The theoretical and practical interest represents the analysis of the
possibility of code redundancy evaluation basing on its a priori statistical
characteristics, that is, the a priori probabilities of generating of the code
alphabet symbols on the output of the transmitted data source. In [5] the
authors defined correlation properties of the code and got algorithms for the
redundancy factors calculation using a priori probability characteristics of K-ary alphabet:
a)
algorithm for calculating the normalized
autocorrelation coefficients:
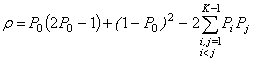, (11)
where P0 and Pi (Pj) are the probabilities of occurrence of zero and
non-zero symbols in the output information source (input channel),
respectively;
b)
algorithm for calculating the normalized
autocorrelation coefficients for the case of code without zero signal sign:
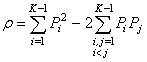; (12)
c)
algorithm for calculating the factors of
redundancy for the case of code without zero signal sign:
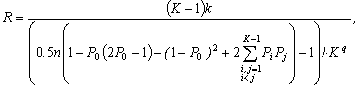(13)
were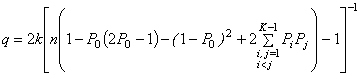 
;
d)
algorithm for calculating the factors of
redundancy for the case of code without zero signal sign:
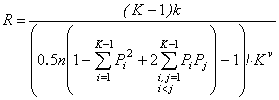, (14)
were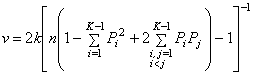 
.
4. RESULTS
Thus, the main results of the work are:
a)
calculation of metric characteristics of
non-binary code PR-sequences that are different from the classic ones by the
higher potential level of noise immunity;
b)
algorithms for calculating the code
redundancy factors using the values of minimum code distance, the multiplicity
of transformation or erase error correction, the normalized autocorrelation
coefficients, and a priori statistical characteristics for channels with
transformation or erase errors.
The obtained results allowed to
develop algorithms and software for the simulation of the non-binary
information channels with PRS codes. The model enabled a wide range of research
and allowed to get almost full range of data needed to evaluate the errors of
the synthesized calculation formulas and make the plots of relations.
The obtained algorithms were tested by computer simulation. As a result,
the accuracy of the above relationships was estimated. The graphs of code
redundancy factor versus minimum code distance, the multiplicity of corrected
transformation or erasure errors, normalized autocorrelation coefficients, the
values of a priori probabilities of generating symbols of a code alphabet used
on the output of the primary information source were built.
As an example, the Figure 2 gives
the dependence of the code redundancy factor on the minimum code distance
calculated by the relationships for the boundaries of redundancy by Hamming,
Varshamov-Gilbert and Plotkin for a fixed number of data symbols.
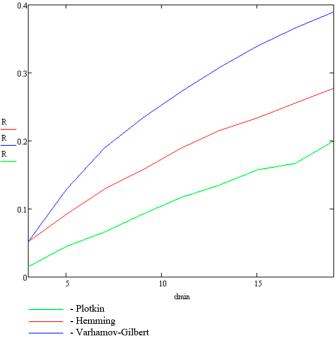
Figure
2. Graphs of code redundancy from the minimum code distance
References:
1. S.
Martorell, Soares C. Guedes, J. Barnett (Eds) Safety, Reliability and Risk Analysis:
Theory, Methods and Applications. Proceedings of the European Safety and
Reliability Conference, ESREL, 2008.
2. W. Liu
Introduction to Hybrid Vehicle System Modeling and Control. Inc., Hoboken, New
Jersey, 2013. – 429 p.
3. G. E. P.
Box, G. M. Jenkins, G. C. Reinsel Time Series Analysis: Forecasting and
Control. Upper Saddle River, NJ: Prentice–Hall, 1994.
4. M. B.
Priestley Spectral analysis and time series. London, New York: Academic Press,
1982.
5. M. S.
Svetlov, Yu. A. Ulyanina «The relationship between the redundancy and the
statistical properties of ternary and K-ary PRS- codes», ATM-2011 [text]: Wed.
the II International. Scientific. Conf. 2 vols. 2 vol. Section 2 / Saratov:
Publishing House "Wright-Expo", 2012. - P. 63-66. [in Russian].