Ташенова Ж.М., Кудайкулов А.К.

PhD докторант, Евразийский национальный университет имени Л.Н. Гумилев, Астана

д.ф.-м.н..профессор, Евразийский национальный университет имени Л.Н. Гумилев, Астана

Вычислительный алгоритм математическая модель термо - напряженного состояния частично теплоизолированного стержня переменного сечения и ограниченной длины при воздействии источников тепла

Несущие элементы многих технологических конструкций являются частично теплоизолированными по боковой поверхности и жестко защемленными двумя концами. Кроме того, из-за потребности технологии эти стержневые элементы являются переменными поперечными сечениями. Поэтому, если профиль поперечного сечения является круг, то радиус является зависимой от координаты, т.е. . Предположим, что радиус поперечного сечения рассматриваемого частично теплоизолированного стержня меняется линейно по ее длине, т.е. , где , . При воздействии разнообразных источников тепла, т.е. при одновременном наличии локальной температуры, теплового потока, теплообмена а также точечных внутренних источников тепла по длине стержня распределяется поле температур с некоторым законом . При наличии поле распределения температуры выражение потенциальной энергии упругой деформации рассматриваемого стержня имеет следующий вид [1].

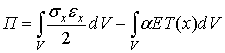(1.3.1)

где - поле распределение упругого перемещения по длине рассматриваемого стержня, - упругая составляющая деформации, E- модуль упругости материала стержня, - коэффициент теплового расширения материала стержня, - упругая составляющая напряжения, V- объем стержня.

Учитывая, что рассматриваемый стержень имеет форму усеченного конуса, определим выражение его объема

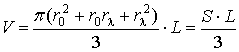(1.3.2)

где и - соответственно радиусы поперечных сечений левого и правого концов стержня, - длина рассматриваемого стержня, (рисунок 1.3.1).

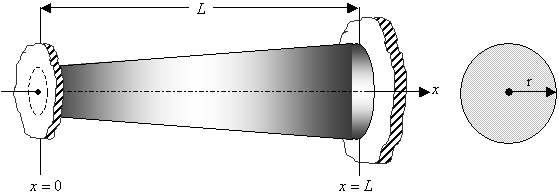
Рисунок 1.3.1 – Расчетная схема задачи

Учитывая, что процесс распределения поле температур по длине рассматриваемого стержня является установившимся, поле распределение упругого перемещения в пределах длины одного дискретного квадратичного элемента длиной аппроксимируем полным полиномом второго порядка

, (1.3.3)

где n- число дискретных квадратичных элементов. Поля распределения упругого перемещения в пределах одного квадратичного дискретного элемента, представляя как кривой, проходящей через трех равностоящих узлов по аналогии (1.1.9) имеем

(1.3.4)

где , , – функции формы для квадратичного дискретного элемента с тремя узлами, которые определяются формулой (1.1.8), , и – узловые значения упругого перемещения (рисунке 1.3.2)

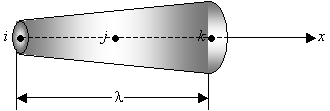
Рисунок 1.3.2 – Дискретный квадратичный элемент с тремя узлами

, , (1.3.5)

Здесь локальная система координат для квадратичного дискретного элемента с тремя узлами (рисунок 1.3.1). Поле распределение упругого составляющего деформации в пределах каждого квадратичного дискретного элемента имеет следующий вид

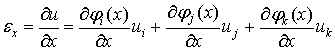
или пользуясь соотношениями (1.1.8) имеем

(1.3.6)

Для одного квадратичного дискретного элемента потенциальная энергия упругой деформации в соответствии (1.3.1) имеет следующий вид

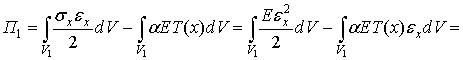
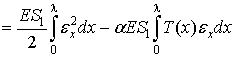(1.3.7)

где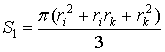

В выражении (1.3.7) интегрируя каждый интеграл, получим выражение потенциальной энергии упругой деформации одного квадратичного дискретного элемента получим ее интегрированный вид

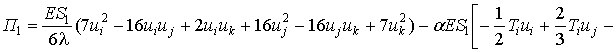
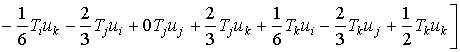(1.3.10)

Общий вид функционала выражающую потенциальную энергию упругой деформации рассматриваемого стержня переменного сечения ограниченной длины и защемленного обоими концами будет следующим

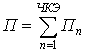(1.3.11)

где ЧКЭ- общее число квадратичных дискретных элементов в рассматриваемом стержне.

Здесь при , значение i, j, k определяется следующим образом , , . Далее при , значения i, j и k определяются по схеме , , .

Минимизируя потенциальную энергию упругой деформации (1.3.11) рассматриваемого стержня по узловым значениям упругого перемещения, строится математическая модель термо-напряженного состояния защемленного обоими концами стержня переменного сечения и ограниченной длины, в виде следующей разрешающей системы линейных алгебраических уравнений

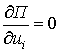, (1.3.12)

Решая эту систему численным методом Гаусса стоится поле распределения упругого перемещения , по длине стержня.

После чего, определяется поле распределения упругих составляющих деформаций и напряжений в соответствии законов Коши и Гука [2]

, (1.3.13)

На основе законов термодинамики [3] строится поле распределения температурного составляющих деформаций и напряжений

, (1.3.14)

Тогда поле распределения термоупругих составляющих деформаций и напряжений [4]

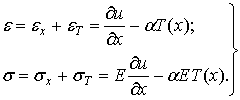(1.3.15)

Значения составляющих деформаций и напряжений определяются на середине половины (между соседними узлами) каждого квадратичного дискретного элемента.

Исходя из написанного видно, что при определении поле распределении температуры число дискретных элементов должно быть два раза больше чем при определении поле упругих перемещений. Разработанная математическая модель и вычислительный алгоритм определения поля перемещения в стержне ограниченной длины жестко-защемленной одним концом при наличии источников тепла и осевой силы.

Литература:

1. И.А.Биргер, Я.Г.Пановко. Прочность.Устойчивость.Колебания. Том1. //М.: Машиностроение, 1968. -114-115 стр.

2. Постнов В.А. Харкурин И.Я. Метод конечных элементов в расчетах судовых конструкций.- Л.:Судостроение,1974. –344с.

3. Ноздрев В.Ф. Курс термодинамики. Просвещение. 1967. 248 с.

4. И.А.Бергер, Я.Г. Пановко. Прочность.Устойчивость. Колебания. Том–1. Изд-во «Машиностроение», М.: 1968г.,568 с.