Технические науки/4. Транспорт

Д.т.н. Савоськин А. Н., к.ф.-м.н. Ляпушкин Н. Н., к.т.н. Чучин А. А.

Московский государственный университет путей сообщения, Россия

Прогнозирование характеристик сцепления колес локомотивов с рельсами

В настоящее время характеристики сцепления определяют по результатам испытаний построенных образцов. На основе этих результатов были получены и уточнены зависимости силы сцепления колеса локомотива с рельсом от скорости движения, которые вошли в правила проведения тяговых расчетов (ПТР), и зависимости силы сцепления (коэффициента сцепления) от относительной скорости скольжения колеса по рельсу. Было установлено влияние на величину силы сцепления влажности и температуры воздуха, загрязнения рельса, наличия песка на нем и т. п. Однако не были разработаны модели, рассматривающие физические процессы при контакте колеса с рельсом. Поэтому все зависимости коэффициента сцепления от скорости движения, скорости скольжения, влияние песка, загрязнений, температуры окружающего воздуха, влажности, атмосферного давления и т. п. носят сугубо феноменологический характер и не позволяют решать задачи прогнозирования сцепных свойств проектируемых локомотивов.

Вместе с тем, в силу значительных нормальных и тангенциальных давлений, действующих между колесом и рельсом, при определении силы сцепления необходимо учитывать взаимодействие, возникающее на площадке их контакта на атомном уровне. Поэтому для объяснения явления сцепления необходимо рассматривать процессы, происходящие в пятне контакта, с позиций физики твердого тела и термодинамики неравновесных процессов. С этой целью необходимо использовать фундаментальное понятие физики твердого тела о дислокациях – несовершенствах кристаллической решетки металла, обусловленных отсутствием одного из атомов в ее ряду. Под действием приложенных нагрузок эти дислокации могут перемещаться и выходить на поверхность кристалла или детали если выполняется условие Мизеса [1]:

, (1)

в соответствие с которым выход дислокаций на поверхность возможен если сумма квадрата нормальных давлений и утроенного значения квадрата касательных напряжений превышают квадрат предела упругости материала .

Проверим, выполняется ли это условие для колеса локомотива, передающего на рельс вертикальное давление 115 кН и реализующего силу тяги 40 кН. Поскольку площадка контакта колеса и рельса имеет вид эллипса большая полуось которого составляет a=8·10^–3 м, а малая b=6·10^–3 м, то площадь такого эллипса будет равна 1,5·10^–4 мм, а величина нормального напряжения будет равна 767 МПа, что близко к пределу упругости рельсовой стали. Таким образом, реализация даже небольшой величины силы тяги обеспечит выполнение условия (1) и вызовет появление деформации сдвига, сопровождаемой выходом дислокаций на поверхность контакта колеса и рельса.

Выход дислокации на поверхность сопровождается выделением такого же количества энергии во внешнюю среду, как и затраты, потребные на ее перемещение. По данным [2] эта энергия составляет 8 эВ. Кроме того, в [2] показано, что большая часть деформации кристаллической решетки является неоднородной на протяжении нескольких элементарных ячеек. Это говорит о том, что на поверхности металла вблизи точек выхода дислокации имеются области, деформация которых выходит далеко за пределы упругости и атомы этой области на поверхности металла слабо связаны с атомами в объеме.

Для решения практических задач в теории дислокаций большое значение имеет величина концентрации дислокаций. Эту концентрацию принято определять как число дислокационных линий, пересекающих единичную площадку внутри кристалла. Анализируя экспериментальные работы, Ч. Киттель [2] приводит возможные значения концентрации дислокации 10²÷10³ см^-2 в наиболее совершенных оптически чистых кристаллах, и 10¹¹÷10¹² см^-2 в сильно деформированных кристаллах.

По данным Б. Авербаха [3] концентрация дислокаций в процессе деформации увеличивается в 10³ раз. Кроме того, если одна дислокация проходит вдоль всей плоскости, то это должно вызывать на поверхности смещение одной атомной плоскости, тогда как в действительности, смещенными на поверхности оказываются в 10²÷10³ раз больше плоскостей. Для объяснения этого эффекта У. Франк и В. Рид предложили модель «размножения (генерации) дислокаций» [4], механизм которой подобен размножению мыльных пузырей. В этой работе найдено значение энергии активации обменного процесса при объединении поверхностных атомов, в предположении, что атомы на поверхности соприкосновения, образовавшиеся за счет выхода дислокации, являются квазисвободными. Значение этой энергии составляет менее 1 эВ.

Таким образом, энергия активации обменного процесса при объединении квазисвободных атомов активного центра на поверхности рельса с атомами колеса, примерно на порядок меньше запаса энергии в результате выхода дислокации на поверхность. Это означает, что процесс установления физического взаимодействия между атомами колеса и рельса протекает самопроизвольно, при условии наличия активных центров на поверхности рельса (тангенциального давления со стороны колеса на рельс) и отсутствия окисной пленки на поверхности рельса.

Рассмотрим образование окисных пленок на рельсе, а так же условия их разрушения, поскольку, физическое взаимодействие между атомами колеса и рельса при наличии пленок на поверхности рельса, невозможно. Молекула кислорода, попадая на металл, расщепляется на атомы, которые химически взаимодействуют с металлом и образуют с ним очень прочные направленные связи.

Через пленку толщиной δ электроны из металла переходят к кислороду, адсорбированному на внешней стороне пленки. Это перемещение объясняется туннельным переходом электрона через потенциальный барьер, которым является тонкий слой окисной пленки. В области металл – окисная пленка образуется p–n переход. Молекулы воды, попав на пленку, поляризуются полем p–n перехода. Небольшое количество молекул воды, создающее несколько мономолекулярных слоев на поверхности, приводит к увеличению толщины пленки и затруднению туннельного эффекта. Дальнейшее увеличение количества молекул воды приводит к еще большому утолщению пленки и при δ>1∙10^-8 м наступает разрушение двойного электрического заряда. При этом сама окисная пленка за счет поляризации атомов воды частично разрушается и на поверхности металла остается только тонкий слой хемосорбционной пленки. Из работ Ю. М. Лужнова [5] известно, что количество влаги на рельсе по-разному влияет на величину силы сцепления колеса с рельсом. При малом количестве влаги сцепление уменьшается (окисная пленка увеличивается). С увеличением количества влаги сцепление возрастает так, как окисная пленка уменьшается.

При отрицательных температурах молекулы воды превращаются в лед. При этом происходит увеличение объема пленки, за счет «сдвига» молекул окиси и образование на основе поляризованных молекул воды хемосорбционной связи металл – молекула льда. Данная связь носит направленный характер и поэтому значительна, однако, кристаллы льда очень хрупки и избавиться ото льда легче ударной нагрузкой, а не сдвиговым напряжением.

На основе изложенного, путем аппроксимации было получено соотношение, с помощью которого возможно определить разрушение пленки по отношению Λ_р величины поверхности разрушения пленки ∆S, к величине рассматриваемой поверхности S_0. Зависимость этого отношения от температуры T ^oС, выраженной в градусах Цельсия, можно представить в виде:

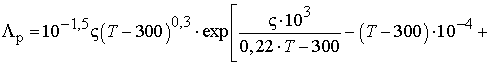
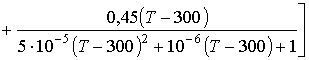(2)

где ς=1,150.

Для устранения с поверхности рельса органических пленок в практике железнодорожного транспорта используют кремневый песок. Частицы двуокиси кремния достаточно тверды и их линейные размеры составляют от 0,2 до 2 мм. На поверхность загрязненного рельса при буксовании колес локомотива подается песок, тем самым кратковременно увеличивается зазор h между колесом и рельсом, причем h>0,1 мм. Это означает, что удаление органики из зазора при наличии песка происходит при незначительном сдвиговом воздействии со стороны колеса локомотива. Удаление таким способом масляных пленок с поверхности рельса иногда приводит к созданию поверхностей по своим свойствам близким к ювениальным, что создает условия для образования большего числа захватов на контактной площадке и резкому изменению скорости скольжения колеса.

При наличии песка на поверхности рельса, покрытого льдом, из-за неравномерной дисперсности песка на площади, занимаемой им на рельсе, появляется дополнительная переменная вертикальная составляющей силы, действующая со стороны колеса на рельс. В результате происходит растрескивание льда и очищение от него рельса.

Из экспериментов известно, что очистка поверхности металлов от пленки может осуществляться приложением к ней нормальной нагрузки, не превышающий предел упругости. Поскольку вертикальное давление, передаваемое от колеса локомотива на рельс, превышает предел упругости рельсовой стали, то происходит самопроизвольная очистка (частичная) поверхности рельса при движении локомотива.

Таким образом, факторами, приводящими к разрушению окисных пленок на поверхности рельса с находящимися на них загрязнениями, являются высокое давление со стороны колеса, различие в объемных деформациях и коэффициентах теплового расширения, а также скольжение колеса по рельсу. Это означает, что на поверхности рельса в пятне контакта имеются условия для установления физического контакта между колесом и рельсом.

Физическую модель сцепления колеса с рельсом разработаем на следующих принципах:

– сцепление колеса с рельсом определяет микропроцесс, происходящий на контактной площадке, представляющий собой взаимодействие группы атомов колеса и рельса (захват), осуществляемый в результате образования активных центров на поверхностях колеса и рельса за счет действия на них нормального и тангенциального давления;

– окисная пленка, имеющаяся на поверхности рельса с нанесенными на ней загрязнениями, в процессе скольжения колеса по рельсу разрушается из-за нагрева и различий величин коэффициентов теплового и объемного расширения рельса и окисла;

– величина силы сцепления определяется силой разрушения захватов, имеющихся в данный момент времени на контактной площадке.

В работе решена задача определения температуры поверхностных слоев рельса с учетом того, что процессы сцепления и скольжения являются термодинамически неравновесными, охватывающими ограниченную область колеса и рельса (пятно контакта) и глубину прогревания, а также времени. В силу этого, параметры среды в ограниченной области меняются незначительно, и их можно считать постоянными. Поэтому применим интегральный подход (поверхность контакта колесо − рельс рассмотрим как одно целое) к определению температуры поверхности контакта колеса и рельса. Такой подход, в отличие от дифференциального, позволяет рассмотреть задачу определения температуры на поверхности контактной площадки при движении источника тепла со скоростью v. Найдем диссипативную часть работы А, затраченную на реализацию силы тяги, приложенной к колесу. Эта работа определяется вращающим моментом, действующим на колесо M_вр и углом поворота колеса при проскальзывании φ_ск:

А=M_врφ_ск≈F_кrφ_ск. (3)

Теплота Q, выделившаяся при этом на поверхности в зоне контакта колесо – рельс, равна:

Q=СmΔT=Cρ2b(v+v_ск)t_скδΔT, (4)

где F_к – сила тяги, приложенная к колесу; r – радиус колеса; С=450 дж/кг·град – удельная теплоемкость стали рельса; ρ =7,7·10³ кг/м³ – плотность стали рельса; b≈6·10^-3 м – поперечная полуось пятна контакта; v – скорость движения колеса; t_ск=rφ_ск/v_ск – время скольжения; v_ск –скорость скольжения колеса; δ – глубина поступления тепла в рельс за время t_δ=2a/v (a – продольная полуось пятна касания, равная 8 мм); ΔT=T−T₀, (T₀=300 К – нормальное термодинамическое условие).

Процесс взаимодействия точек колеса локомотива и рельса на пятне контакта является адиабатическим, поскольку составляет миллисекунды. В связи с этим приравняем величины А и Q и из полученного равенства найдем разность температур ΔT, считая, что половина выделявшегося тепла перейдет в колесо:

ΔT=F_кv_ск/4Cρbδ(v+v_ск). (5)

Учитывая, что на поверхности рельса имеются окисные пленки с загрязнениями, являющиеся экраном для поступления тепла в рельс, это тепло поступает в рельс по “мостикам” между колесом и рельсом, возникающим в результате захватов. Толщины наклепанного слоя, как следует из работ Б. Г. Лившица и С. И. Губкина [6] не превышают δ₀≈(4÷10)·10^─3 м. В этом слое существует значительный градиент напряжений, затрудняющий распространение тепла. Поэтому можем принять, что глубина распространения тепла за время экспозиции колеса, равное миллисекундам, не превышает δ₀≈10^-4 м. После подстановки в выражение (7) исходных данных, имеем

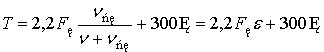, (6)

где e – относительная скорость скольжения:

.

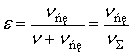На рис. 1 представлена зависимость температуры поверхности рельса T от скорости скольжения v_ск и скорости движения v при заданном значении F_к=50 кН. Относительная скорость скольжения e изменяется при этом в пределах от 0 до критической величины e_кр, при которой происходит срыв сцепления.

Отметим, что при значении e близком к e_кр, температура поверхности рельса приближается к 1000К. Приведенное значение температуры при e_кр близ-

v_ск, м/с м/с

v, м/с

T, K

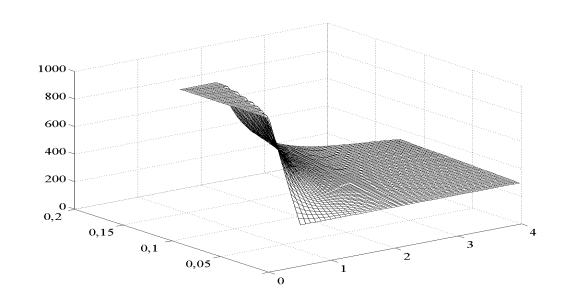
Рисунок. 1. Зависимость температуры поверхности рельса T от скорости скольжения v_ск и скорости движения v колеса локомотива

ко к температуре рельса, измеренной экспериментально Л. В. Гойхманом, А. Л. Дроновым и Н. Д. Желевым [7].

Глубина распространения тепла в рельс при температуре выше температуры Дебая (для стали ≈560 К) увеличивается пропорционально температуре, в соответствии с законом Дюлонга-Пти. При температуре близкой к 1000 К и выше, поверхность рельса очищена от загрязнений и происходит частичный отпуск поверхностного слоя, глубина прогревания не будет постоянной и выражение (6) примет следующий вид:

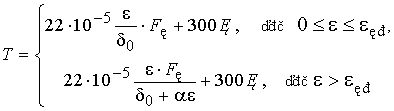, (7)

где a=0,25·10^-2м.

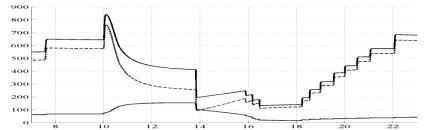
На рис. 2 представлена одна из зависимостей семейства кривых Т=f(e ) в координатах температура поверхности рельса T – относительная скорость скольжения ε.

Рисунок 2. Зависимость температуры поверхности рельса T от относительной скорости скольжения

Как видно из рис. 2, при ee_кр температура линейно нарастает в зависимости от e. При e>e_кр температура в зоне контакта уменьшается за счет увеличения глубины распространения тепла в рельсе, что приводит к частичному процессу рекристаллизации наклепанного поверхностного слоя.

Как следует из (1), трансляционная пластическая деформация тела наступает при значении критического напряжения, определяемого условием Мизеса. Как будет показано далее, при движении локомотива условие Мизеса выполняется, т. е. происходит трансляционная пластическая деформация в пятне контакта. Это означает, что при движении локомотива со стороны колеса на рельс действует сила тяги F_к(), обусловленная его вращательным моментом, вызывающая движение дислокаций в поверхностных слоях рельса.

В силу консервативности силового поля в объеме и на поверхности материала рельса движение дислокаций происходит под действием силы F_к(), и силы давления со стороны колеса П за счет увеличения потенциальной энергии кристаллической решетки ΔE_п.

Прохождение дислокации в материале и выход ее на поверхность эквивалентно сдвигу в кристаллической структуре материала рельса на величину ее постоянной Δr ≈10^-13 м. Тогда ΔE_п равна:

.

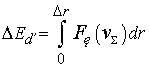В пределах постоянной решетки Δr сила F_к() постоянна. Примем ее равной наибольшей величине F_кб=50 кН. Тогда наибольшее увеличение потенциальной энергии решетки составит ΔE_пб=F_кбΔr ≈5·10⁻⁹ Дж.

Энергия от выхода на поверхность одной дислокации составляет ΔE_i=8 эВ=1,3·10⁻¹⁸ Дж. Тогда число дислокаций, вышедших на поверхность за счет действия силы F_кб со стороны колеса, равно:

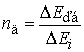=3,8·10⁹. (8)

Концентрация дислокаций при постоянном тангенциальном давлении определяется, как

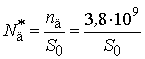, (9)

где a и b − длины полуосей эллипса пятна контакта: a=6·10⁻³ м, b=8·10⁻³ м; S₀ – площадь пятна контакта: S₀=πab≈1,5·10⁻⁴ м². После подстановки этих величин в выражение (9) получим:

≈2,5·10¹¹ м^-2 . (10)

Концентрацию дислокаций в общем случае можно представить виде:

N_д≈2,5·10¹¹F_{к .} (11)

В данном выражении зависимость F_к является тяговой характеристикой асинхронного или синхронного тягового электродвигателя переменного тока, а также коллекторного тягового электродвигателя постоянного тока с последовательной или независимой системами возбуждения.

Закон движения дислокаций в общем случае зависит от числа различных типов несовершенств кристаллической структуры. В нашем случае рассматривается динамика движения дислокации в материале с наклепом, который характерен для поверхностных слоев рельса. В этом случае инерционной составляющей, которая определяет закон движения дислокации, будет внутреннее напряжение в материале σ_вн, обусловленное наклепом, достигающее величины σ_вн≈10⁵÷10⁶ Па. С учетом процесса движения дислокаций уточним выражение для концентрации дислокаций на поверхности, введя в (11) дополнительный множитель, учитывающий это явление:

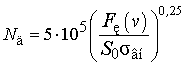, (12)

где − площадь пятна контакта.

Допустим, что скорость деформации рельса равна скорости движения локомотива v. Увеличение v приводит к появлению дополнительного числа дислокаций на поверхности, что объясняется возрастанием скорости генерации дислокаций в “источнике Франка и Рида”.

Такое увеличение числа дислокаций в зависимости от скорости пластической деформации определяется коэффициентом m. Эта зависимость носит параболический характер со слабо выраженным максимумом при v»100 км/ч. Подобная скорость деформирования металла наблюдается при сварке ультразвуком.

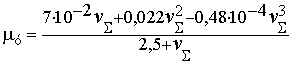. (13)

С учетом этого, окончательное выражение для концентрации дислокаций на поверхности примет вид:

. (14)

На основе выражения (2) в работе с учетом (6) получена зависимость коэффициента разрушения пленки (Λ_р=, от относительной скорости скольжения ε:

Λ_р(e)=(ε) ^0,3exp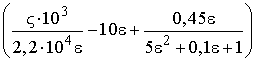. (15)

Отличительной особенностью характеристики сцепления колеса с рельсом является рост силы сцепления с увеличением скольжения колеса по рельсу, что свойственно только металлическим колесу и рельсу. Причиной этого является трансляционное пластическое течение кристаллической структуры рельса, возникающее за счет “схлопывания” дислокаций.

В связи с тем, что система колесо − рельс является замкнутой, разрушение захватов приводит к возникновению силы сцепления, и одновременно действует на поверхность рельса в направлении по движению локомотива, вызывая сдвиг атомных слоев вблизи поверхности рельса.

Принципы построения модели скольжения колеса по рельсу:

− скольжение колеса по рельсу в режиме тяги происходит за счет трансляционного пластического течения поверхностных слоев материала рельса, возникающего при «схлопывании» дислокаций, вышедших на поверхность;

− трансляционное пластическое течение (сдвиг) поверхностных слоев происходит под действием тангенциального давления, со стороны колеса, величина которого определяет скорость скольжения колеса по рельсу;

− величина тангенциального давления численно пропорциональна силе разрушения захватов, действующей на активную поверхность контактной площадки.

В соответствии с этими принципами выразим величину скорости скольжения колеса локомотива по рельсу в виде

, (16)

где – суммарная величина трансляционного пластического течения на поверхности рельса, наступающего в результате действия тангенциальной силы, превышающей критическое значение тангенциального давления τ, определяемое из условия Мизеса (1); – время экспозиции колеса на пятне контакта, которое в соответствие с пояснениями к (13) равно

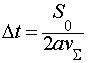. (17)

Величина определяется количеством дислокаций , вышедших на поверхность рельса, а также сдвигом в структуре материала рельса на величину постоянной ее атомной решетки Δr ≈10⁻¹³ м.

.

С учетом (16) и (17) величину скорости относительного скольжения можно определить как:

=2·10^-13 . (18)

Таким образом, нами сформулированы основные принципы построения физической модели сцепления, в основу которого положен процесс разрушения “захватов”, и процесса скольжения колеса по рельсу на основе трансляционного пластического течения материала колеса и рельса на контактной площадке.

Рассмотрим результаты расчета кривых сцепления и проверки адекватности предложенной модели сцепления и скольжения.

На рис. 3 представлена зависимость относительной скорости скольжения колеса локомотива от величины силы тяги и скорости движения (кривые 1 и 2), и “следы” этих кривых 1’и 2’; 1’’и 2’’; 1’’’и 2’’’в координатах [F_к;], [ε; ] и [ε;F_к].

У локомотива с последовательным возбуждением ТЭД при увеличении силы тяги от 10⁴ Н до 8,1·10⁴ Н значительно меняется величина относительной скорости скольжения от 0,014 до 0,029. При этом рост ε сопровождается уменьшением суммарной скорости, т. е. увеличивается скорость скольжения (рис. 3, кривая 1 и 1’’).

Относительная скорость скольжения у локомотива с независимым возбуждением практически не зависит от силы тяги (рис. 3, кривая 2 и 2’’’). Кроме того, при уменьшении суммарной скорости и увеличении силы тяги величина ε

Рисунок 3. Зависимости относительной скорости скольжения колеса локомотива от

величины силы тяги и скорости движения для локомотив с ТЭД

последовательного 1 и независимого 2 возбуждения:

в координатах [F_к;v] − кривые 1´и 2´; [ε;v] − кривые 1´´ и 2´´; [ε;F_к] − 1´´´ и 2´´´

увеличивается с 0,019 до 0,022, это означает, что скорость скольжения увеличивается на малую величину. Анализ полученной кривой свидетельствует о практически постоянной скорости движения локомотива с независимой системой возбуждения ТЭД при увеличении силы тяги.

В соответствии с принципами построения модели выразим силу сцепления в виде:

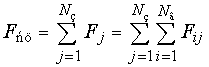, (19)

Здесь j – число пятен захвата на контактной площадке, i – число взаимодействий между атомами колеса и рельса в одном пятне захвата, F_j – суммарная сила взаимодействия в одном захвате, N₃ – число захватов, N_в – число взаимодействий между атомами колеса и рельса в одном захвате, F_ij – сила взаимодействия между двумя атомами колеса и рельса:

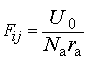. (20)

Здесь U₀ – энергия связи одного моля в металле (U₀= 2,5·10⁴ Дж/моль), N_a – число Авогадро (N_a=6,02·10²³ моль^-1), r_a –расстояние между взаимодействующими атомами примем равной диаметру первой Боровской орбиты (r_a ≈2,3·10^–10 м).

Примем, что число пятен захвата определяется концентрацией дислокаций на поверхности N_д(F_к), тогда

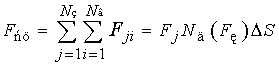, (21)

где ― сила взаимодействия в одном захвате

.

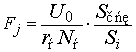В этой формуле S_иск − площадь искажения – площадь, в пределах которой атомы, находящиеся на поверхности колеса и рельса, слабо связаны с атомами внутри объема. Эту площадь в первом приближении можно считать площадью круга радиусом r_иск ≈ 3·10⁻⁶ м.

S_i – площадь взаимодействия i-того атома в j-том захвате

,

где r₀ – возможный радиус взаимодействия атомов поверхности колеса и рельса за счет выхода одной дислокации (r₀ ≈3·10⁻¹⁰ м);

При этих значениях r₀ и r_иск отношение =10⁸.

Сведем полученные соотношения в единое уравнение, решение которого позволяет определить коэффициент сцепления , здесь П – вертикальная нагрузка, передаваемая от колеса на рельс:

, (22)

где и Λ_р(e) определяются соответственно выражениями (14) и (15).

Выражение (22) позволяет построить поверхности сцепления в зависимости от скоростей движения и скольжения для двигателей с различными системами возбуждения (рис.4), поскольку множитель , входящий в (22) и определяющий концентрацию дислокации в пятне контакта, является функцией тяговой характеристики электродвигателя.

v_ск, м/с

2

1 сцепления для двигателей с независимым и последовательным возбуждением, представленных на рис. 9, объясняется различием кривым F_к=f(v) для этих двигателей.

ψ_сц

v, м/с

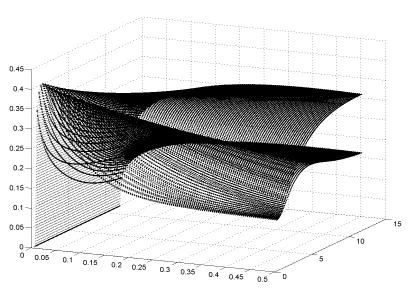
Рисунок. 4. Зависимости коэффициента сцепления от скорости скольжения колеса по рельсу и скорости движения локомотива:

поверхность 1 − для локомотива с ТЭД последовательного возбуждения;

поверхность 2 – для локомотива с ТЭД независимого возбуждения

При этом поверхность (1) для тягового электродвигателя (ТЭД) последовательного возбуждения лежит ниже, чем аналогичная поверхность (2) для локомотива с ТЭД независимого возбуждения. Кроме того, поверхность (2) слабо зависит от скоростей движения и скольжения, что соответствует эксплуатационным испытаниям и содержит практически два максимума. Это свидетельствует о высоких противобуксовочных свойствах локомотивов с тяговыми электродвигателями независимого возбуждения, что также подтверждается практикой эксплуатации таких локомотивов. Отличие поверхностей коэффициента сцепления для тяговых электродвигателей с независимым и последовательным возбуждением, объясняется различием кривым F_к=f(v) для этих двигателей.

Аналогичный вид имеет поверхность коэффициента сцепления [13], построенная по результатам испытаний электровоза S252 фирмы «Сименс» с асинхронными тяговыми двигателями (рис.5, а). Для более детального сравнения на рис. 5, б приведена такая поверхность, полученная на основе перестроения поверхности 2 (см. рис. 4) в координатах рис 5,а. Поверхности сцепления, приведенные на этих рисунках, имеют сходный характер. Их отличия объясняются тем, что рис. 5, а построен для электровоза с асинхронными тяговыми двигателями, а рис. 5, б – для электровоза с коллекторными тяговыми двигателями независимого возбуждения.

Рис. 5. Зависимости коэффициента сцепления от относительной скорости скольжения и скорости движения локомотива: а – по экспериментальным данным, приведенным в [13] для электровоза с асинхронными тяговыми электродвигателями;

б – по результатам выполненных расчетов для электровоза с коллекторными тяговыми электродвигателями независимого возбуждения

Рассмотрим поверхность ψ_сц=f(v,v_ск), представленную на рис. 4, в начале как совокупность кривых в плоскости [ψ_сц; v], а затем в плоскости [ψ_сц; v_ск]. Анализ зависимостей коэффициента сцепления от скорости движения колеса при разных постоянных значениях его скорости скольжения показывает следующее: максимальный коэффициент сцепления уменьшается с увеличением скорости движения колеса, что соответствует общепринятым представлениям. Вместе с тем, при больших значениях скорости скольжения колеса падение коэффициента сцепления замедляется с ростом скорости движения.

Зависимости ψ_сц=[f(v_ск)]_v=const свидетельствуют о том, что скорость движения колеса оказывает решающее влияние на процесс его сцепления с рельсом. При малых значениях v вид этих кривых отличается резким снижением ψ_сц после превышения величины скорости скольжения критического значения. С увеличением скорости движения колеса максимум коэффициента сцепления уменьшается, и величина возрастает. Причем с увеличением скорости движения колеса максимум этих зависимостей менее выражен.

На рис. 6 представлены характеристики сцепления – зависимости коэффициента сцепления от относительной скорости скольжения: по экспериментальным данным Ф. Барвела – кривая 1; по результатам расчетов: при последовательным возбуждении ТЭД – пунктирная кривая 2; при независимом возбуж-дении ТЭД – кривая 3.

При этом кривые 2 и 3 были получены путем перестроения соответствующих поверхностей 1 и 2 рисунка 4 в зависимости ψ_сц(ε). Сравнение расчетной характеристик сцепления (кривая 2) с экспериментальной характеристикой (кривая 1) показывает, что коэффициенты сцепления при ε_кр на рассматриваемых кривых практически совпадают, а на восходящей и падающей ветви характеристики несколько отличаются.

ψ_сц

3

2

1

ε

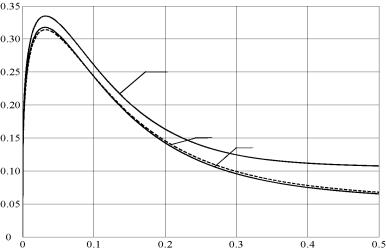
Рисунок 6. Зависимости коэффициента сцепления от относительной скорости скольжения: по экспериментальным данным Ф. Барвела − кривая (1); по результатам расчетов при последовательным возбуждении ТЭД – пунктирная кривая 2; при независимом возбуждении ТЭД – кривая 3

Этот факт можно объяснить двумя причинами. Первая – экспериментальные кривые построены по усредненным замеренным значениям. В ходе экспериментов величина относительной скорости скольжения может оставаться постоянной, при различных значениях скоростей скольжения и движения колеса. Но, как видно из рис. 4, различным скоростям скольжения и движения соответствуют разные значения коэффициентов сцепления. Однако при усреднении значений коэффициентов сцепления этот факт не учитывался.

Вторая причина отличия кривых состоит в том, что изменение значений концентраций дислокаций в поверхностных слоях рельса, вызванные скоростью деформации рельса можно достаточно точно определить, но исходную концентрацию дислокаций можно только оценить.

Как видно из рисунка 6, в целом наблюдается удовлетворительная сходимость представленных на нем расчетной и экспериментальной характеристик сцепления. При сопоставлении кривых 2 и 3 на рис. 6 видно, что при срыве сцепления у локомотива с независимым возбуждением буксование колес значительнее, чем у локомотива с последовательным возбуждением ТЭД. Это факт объясняется видом характеристики ТЭД с независимым возбуждением и также известен из практики эксплуатации локомотивов.

На рис. 7 приведены зависимость ψ_сц(ε) из [13, рис. 10], построенная для электровоза S252 фирмы «Сименс» с асинхронными тяговыми двигателями при движении по сухим рельсам (кривая 1) и зависимость для электровоза с коллекторными тяговыми двигателями независимого возбуждения (кривая 2), перенесенная с рис. 6. Как видно из рис. 7 обе кривые имеют подобный характер. различия между ними объясняются различием в типе тяговых электродвигателей и свидетельствуют о существенных преимуществах по сцепным свойствам электровозов с асинхронными тяговыми двигателями.

Решение уравнения (22) позволяют найти зависимости максимальных значений коэффициента сцепления ψ_бсц от скорости движения локомотива, которые сравнивались с эмпирическими, приведенными в правилах производства тяговых расчетов (ПТР) для трех групп электровозов: 1) ВЛ10, ВЛ11, ВЛ82, ВЛ82^М; 2) ВЛ22, ВЛ23, ВЛ8; 3) ВЛ60, ВЛ80Р, ВЛ80С.

Для этого по данным ПТР и по результатам расчета были построены нормированные кривые сцепления ψ^н_бсц (рис. 8), для указанных трех групп электровозов.

ψ_сц

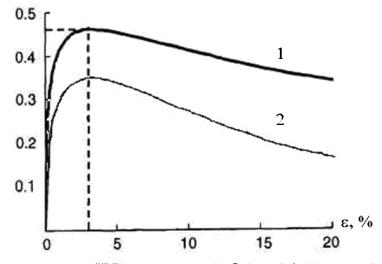
Рисунок 7. Зависимости коэффициента сцепления от относительной скорости скольжения: 1 – по экспериментальным данным, приведенным в [13] для электровоза с асинхронными тяговыми электродвигателями;

б – по результатам выполненных расчетов для электровоза с коллекторными тяговыми электродвигателями независимого возбуждения

,

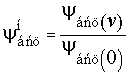где ψ_бсц(0) – значение коэффициента сцепления при скорости движения равной нулю.

ψ_бсц

2

3

11

v, км/ч

Рисунок 8. Нормированные кривые сцепления: полученные экспериментально - сплошные линии; расчетная - пунктирная линия, для трех групп электровозов

1 − ВЛ10, ВЛ11, ВЛ82, ВЛ82^М ; 2 − ВЛ22, ВЛ23, ВЛ8; 3 − ВЛ60, ВЛ80Р, ВЛ80С

Анализ этого рисунка свидетельствует о том, что эмпирические и теоретические нормированные кривые ψ^н_бсц имеют удовлетворительную сходимость. При малых скоростях движения значения ψ^н_бсц мало отличаются для всех групп электровозов. С увеличением скорости движения расхождение возрастает, наибольшее отклонение эмпирических и теоретических нормированных кривых наблюдается для электровозов постоянного тока первой группы. По-видимому, это объясняется высокими погрешностями измерений в экспериментах этой группы, выполнявшихся в 1950÷60 г.г.

В целом зависимости, приведенные на рис. 3÷8, свидетельствуют о корректности предложенной модели процесса взаимодействия колеса и рельса. Будем считать, что предложенная в данной работе модель определяет так называемый потенциальный коэффициент сцепления и не учитывает трибологического состояния поверхностей бандажей и рельсов. Для учета состояния этих поверхностей введем дополнительный трибологический множитель и будем считать, что реализуемый в процессе эксплуатации коэффициент сцепления определяется как:

. (23)

В общем случае, коэффициент представляет собой зависимость атмосферного давления, влажности, температуры, наличия загрязнений на поверхностях катания рельсов и бандажей, тепловой энергии, выделяющейся в процессе взаимодействия колеса и рельса и т. п. Определение такой зависимости представляет собой отдельную задачу, которую следует решать с использованием основных положений триботехники. В рамках настоящей работы ограничимся рассмотрением трех вариантов состояния поверхностей катания рельсов и бандажей:

1). Нормальное не загрязненное состояние поверхностей =1.

2). Режим «наезда» на масляное пятно на поверхности рельса =0,5.

3). Подсыпка песка для восстановления сцепления =1,3.

Эти значения трибологического множителя можно использовать при решении задач по срыву и восстановлению сцепления.

Таким образом, предлагаемая методика обеспечивает возможность прогнозирования характеристик сцепления локомотивов с различными типами тяговых электродвигателей. Ее использование совместно с моделями вертикальных колебаний тележек, крутильных колебаний в их тяговых передачах, а также электромагнитных процессов в тяговом электроприводе локомотива [8, 9, 11] позволяет решать широкий круг задач по реализации сцепления, процессам срыва и восстановления сцепления, работе систем защиты от буксования.

ЛИТЕРАТУРА

1. Mizis T. N.,Mak Farlan J.S. Ahesion of solids and the effect of sun face films ”Procee dings of the Roigal Socity, 202A, n. 1069.

2. Ч. Китель. «Введение в физику твердого тела». М.,Физматгиз, 1963.

3. Averbach B. L., Warren B. E. jorn. Appl. Phys.20 /1066/ 1949/

4. Frank F. C., Read W. N. Phys. Rev. 79, 722, 1957.

5. Лужнов Ю. М. «Сцепление колес с рельсами (природа и закономерность)», М., Интекс, 2003.

6. Лившици Б.Г., Губкин С. И. «Физическое металловедение», М., Металлургиздат, 1963.

7. Гойхман Л. В., Дронов А. Л., Желев Н. Д. «Некоторые результаты исследований термоконтактных исследований» /Труды академии коммунального хозяйства/, городской транспорт, 157, транспорт, 1978.

8. Н. Н. Ляпушкин, А. Н. Савоськин, А. А. Чучин. Моделирование процесса сцепления колеса локомотива с рельсом при шунтировании обмотки якоря тягового электродвигателя последовательного возбуждения. Транспорт Российской Федерации, Санкт Петербург, 2010, №6.

9. Н. Н. Ляпушкин, А. Н. Савоськин, А. А. Чучин. Сравнительный анализ реализации сцепления локомотивов с последовательной и независимой системой возбуждения тягового двигателя. Мир транспорта, Москва, 2010, №4.

10. Н. Н. Ляпушкин, А. Н. Савоськин, А. А. Чучин. Уточнение модели скольжения и сцепления колеса локомотива с рельсом. //Вестник ВЭлНИИ, Новочеркаск, 2011.

11. Н. Н. Ляпушкин. Реализация сцепления локомотива с независимой системой возбуждения тягового двигателя. Мир транспорта, Москва, 2011, №4.

12. Н. Н. Ляпушкин, А. Н. Савоськин, А. А. Чучин. Уточнение модели взаимодействия колеса локомотива с рельсом на основе дислокационной теории пластического течения металлов. Транспорт Урала, Екатеринбург, 2010, №2.

13. O. Polach. Creep forces in simulations of traction vehicles running on adhesion limit. Bombardier Transportation, CH-8401 Winterthur, Switzerland Received 13 June 2003; received in revised form 28 November 2003; accepted 1 March 2004. Wear 258 (2005) 992 – 1000.