Технические науки. Электротехника и радиоэлектроника

Док. тех. наук, проф. Басан С.Н.

Российский государственный гидрометеорологический университет

Филиал в г. Туапсе

Эквивалентные и квазиэквивалентные преобразования нелинейных электрических цепей

В данной работе рассматриваются схемы замещения только таких электрических цепей, элементный базис которых содержит линейные и нелинейные активные сопротивления, ёмкости, индуктивности, линейные управляемые источники (ИТУТ, ИТУН, ИНУН и ИНУТ), а так же независимые источники тока и напряжения[1,2]. Предполагается также, что схему замещения электрической цепи можно представить состоящей из двух частей,- линейной и нелинейной так, как показано на рис. 1.

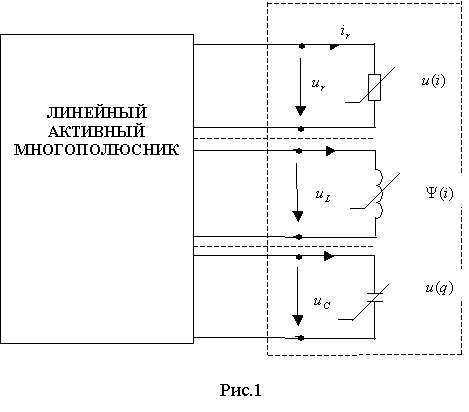
На этом рисунке:

- вектор - столбцы токов нелинейных элементов (сопротивлений, индуктивностей и емкостей соответственно),

вектор - столбцы напряжений нелинейных элементов (сопротивлений, индуктивностей и емкостей соответственно),

- в состав линейного активного многополюсника могут входить линейные элементы всех типов, а также независимые и линейные управляемые источники электрической энергии.

Применив к линейному активному многополюснику теорему об эквивалентном генераторе [1], получим схему замещения на рис.2.

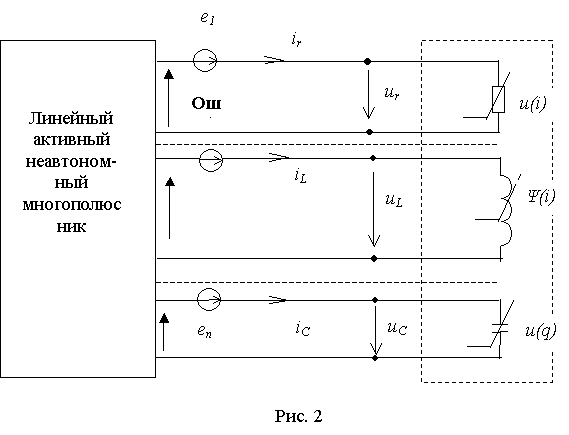
Здесь - ,- независимые источники, напряжение которых равно напряжениям холостого хода, возникающие в местах одновременного обрыва (отключении) нелинейных элементов.

Линейный активный неавтономный многополюсник не содержит независимых источников энергии. Его свойства можно описать следующей системой уравнений:

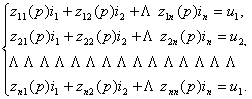(1)

В этих уравнениях:

мгновенные значения переменных (токов и напряжений),

операторные сопротивления,

индексы изменяются в пределах от 1 до n,

оператор дифференцирования, запись означает, что

Для схем замещения, состоящих из двухполюсных элементов, дробно-рациональная функция оператора .

Из второго закона Кирхгофа следует, что каждому свободному члену в системе уравнений (1) соответствует выражение вида

. (2)

Здесь напряжение k-го нелинейного элемента.

Рассмотрим уравнение, соответствующее одной из нелинейных индуктивностей.

. (3)

Разделим обе части уравнения (3) на оператор .

. (4)

Полученному уравнению формально можно поставить в соответствие схему замещения, в которой каждому слагаемому в (4) соответствует напряжение. Подобные преобразования в [4] названы квазиэквивалентными.

Две схемы замещения будем называть квазиэквивалентными, если установлены математические соотношения, позволяющие вычислить по формулам переменные (токи или (и) напряжения) ветвей одной схемы замещения через переменные (токи или (и) напряжения) другой схемы.

Преобразования, позволяющие для заданной схемы замещения получить множество квазиэквивалентных схем замещения, будем называть квазиэквивалентными преобразованиями.

В квазиэквивалентной схеме замещения, соответствующей (4), нелинейной индуктивности соответствует нелинейное активное сопротивление, вольт-амперная характеристика которого численно совпадает с вебер-амперной характеристикой нелинейной индуктивности. Таким образом, (4) можно записать следующим образом:

, (5)

где

рассматривается как сопротивление (квази сопротивление), а - как напряжение источника

, a .

Символом “” будем обозначать численное равенство одной переменной другой переменной, формально считая, что эти переменные имеют одну и ту же размерность.

аналогичные преобразования могут быть выполнены и для уравнений (1) , соответствующих контурам, содержащим нелинейные ёмкости.

, (6)

но

. (7)

Умножим каждый элемент -ого столбца системы (1) на оператор .

Тогда уравнение (1.6) примет вид:

. (8)

Или

. (9)

Выражение можно рассматривать как квазисопротивление, а как квазиток.

Таким образом, в квазиэквивалентной схеме замещения

, (10)

. (11)

Следовательно, уравнение (9) запишется следующим образом:

. (12)

В результате выполненных преобразований уравнения квазиэквивалентной схемы замещения в нелинейной части будут содержать только нелинейные алгебраические уравнения, которым в схеме замещения соответствуют нелинейные резистивные элементы.

В качестве примера рассмотрим схему замещения на рис. 3.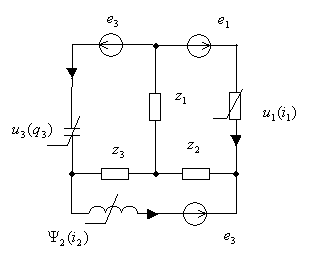

Рис.3.

Используя законы Кирхгофа, уравнения, описывающие процессы в схеме замещения на рис. 3 можно представить в следующем виде:

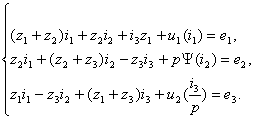(13)

Выполним в этой системе уравнений следующие преобразования, не нарушая соответствующих равенств. Второе уравнение системы (13) разделим на оператор дифференцирования . В первом и третьем уравнении слагаемые, содержащие ток разделим и умножим на оператор . В результате система уравнений (1.17) примет вид (14).

В полученных уравнениях будем считать квази величинами:

, квази ток нелинейной ёмкости, численно равный электрическому заряду ,

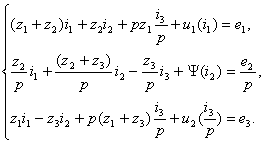(1.14)

,, квази сопротивления, ,,

квази источник напряжения.

В результате система уравнений (14) примет следующий вид:

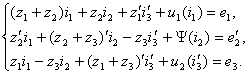(15)

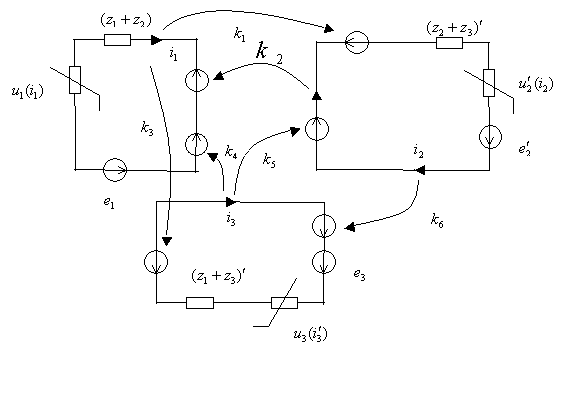
Схема замещения, соответствующая уравнениям (15), полученная в соответствии с [5 ], имеет вид на рис. 4.

Между токами и напряжениями в ветвях схем на рис 3 и 4 существует взаимнооднозначное соответствие, поэтому их можно рассматривать как квазиэквивалентные. В отличие от схемы замещения на рис. 3, в состав схема замещения на рис 4 входят линейные элементы, а из нелинейных элементов только нелинейные резисторы. Проблеме реализации нелинейных резистивных элементов посвящена обширная литература [4,5]. Поэтому на практике реализовать, например, нелинейную ёмкость с заданной кулон- вольтной характеристикой или нелинейную индуктивность с заданной вебер- амперной характеристикой значительно сложнее, чем нелинейный резистивный элемент.

Указанное обстоятельство свидетельствует о том, что нелинейные резистивные цепи занимают особое место в теории нелинейных электрических цепей. Таким образом, задача анализа и синтеза нелинейных резистивных цепей является актуальной.

Литература.

1. Нейман Л.Р. Демирчян К.С. Теоретические основы электротехники. Т.2, Ленинград: Энергоиздат, 1981. с.533.

2. Басан С.Н., Пивнев В.В. Функционально полный элементный базис схем замещения электрических цепей. Известия высших учебных заведений. Электромеханика. 2002 г. с. 21-23.

3. Басан С.Н. Основы теории электрических и электронных цепей. Ч.1, (Основные понятия и определения), Таганрог, ТРТУ, 1995. 136 с.

4.Данилов Л.В. Электрические цепи с нелинейными R-элементами. М. Связь, 1974. 135 с.

5. Басан С.Н.,Пивнев В. В. К вопросу синтеза схем замещения линейных электрических цепей. Известия вузов. Электромеханика. 1999. № 2. с. 8-9.